9주 차
1차시 - 예측 함수 성능 평가
Cost function은 실제 출력(예측 값), Label, regularization으로 이루어져 있다.
테스트 데이터는 학습에 사용되지 않은 데이터로 모델의 성능을 평가할 때 사용되며 잘 작동하면 문제 없지만 오차가 크면 성능 향상이 필요하다.
1. 학습데이터 더 수집하기 : 좋은 생각이나 시간과 노력이 필요하다. 확실하게 파악하고 시작해야함
2. feature 수를 줄인다 : 오버피팅을 방지하기 위해 줄인다.
3. feature 수를 늘린다 : 현재 feature로는 모든 정보를 넘길 수 없을 때 늘린다.
4. 다항식을 추가한다. : 새로운 특징값을 만드는 것과 같다.
5. 정규화 파라미터 감소하기 : train 데이터에 대해 잘 학습한다.
6. 정규화 파라미터 증가하기 : 오버피팅을 해결할 수 있다.
train error를 줄이기 하기 위해 파라미터 수정하기 -> train error가 감소하지만 오버피팅의 결과일 수 있다.
오버피팅이 난 것을 어떻게 알까?
예측 함수를 실제 데이터와 함께 plotting한다. - 이건 feature 수가 많으면 불가능하다.
-> test data에 대한 비용함수 값도 구한다. Logistic regression에서는 비용함수 말고 정확도를 사용할 수 있다.
2차시 - 최적 모델의 선택 ( 데이터 셋 나누기)
다항식은 차수, feature의 수, regularization 파라미터는 몇으로 할지 다양하게 선택해야 한다.
이럴 때 데이터를 Train, Vlidation, Test set(60:20:20)으로 나눈다.
Train : 학습을 위해
Cross Vaildation : 모델 선택을 위해
Test : 최적화된 모델의 일반화 성능 확인
낮은 traning error는 training set에는 잘 된 것이지만, 새로운 데이터 샘플에도 잘 작동한다는 보장이 없다.
학습 데이터에 대해 측정된 오차값은 실제 일반화 오차 ( 일반적 검증이나 test 데이터에서 얻은 오차)보다 뛰어나다.
1~10차까지 다항식으로 만든 신경망을 test 점수가 가장 높은 것을 고르면 될까?
공정한 평가가 아니라네요(test data가 그 차수에 알맞은 data일 수 있다.) - Cross Validation data를 통한 검증!
train data를 통해 학습 후 -> Validation data를 통해 error가 제일 낮은 모델 찾기 -> test data로 마지막 test
3차시 - bias, Variance
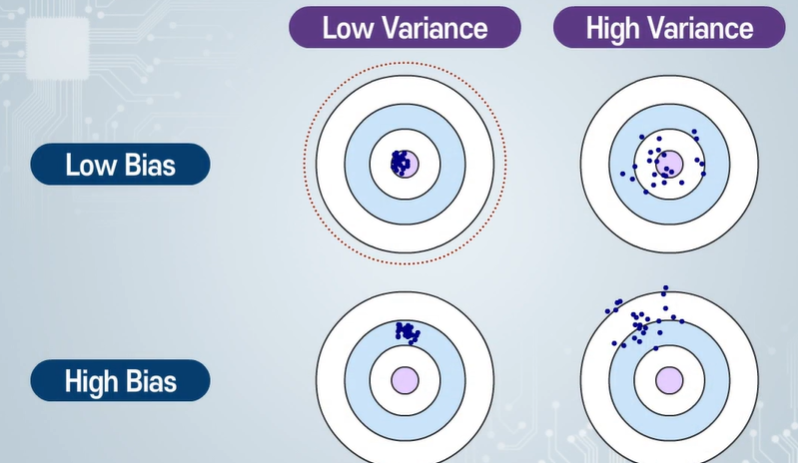
High bias - underfitting - 지나치게 단순해서 데이터의 추이를 따라가지 못한다.
Train,validation 모두 error가 높다. 정규화 항이 높다.
High Variance - overfitting - 지나치게 차수가 높아서 복잡하다.
Train error는 낮은데 Validation error는 높다. 정규화 항이 작다.
적당히 트랜드를 잘 따라간다. == 일반화(Generalization) 성능이 우수하다
차수가 증가함에 따라 학습 오차는 점점 줄어들지만 Validation은 일정 이상이 되면 오차가 늘어난다.
Bias - 모델이 나타내는 예측 값과 실제 값의 차이
올바른 해답을 얼마나 잘 표현할 지 기대할 수 있나.
Variance - 주어진 데이터에 대해서 모델의 예측 값이 얼마나 변동성이 있는지 나타낸 값
모델이 얼마나 민감하게 변동성을 보여주나.

y만 관측이 가능하며, 입실론 때문에 오차가 발생한다.
y의 평균은 h, 분산은 sigma 제곱이 된다.

노이즈의 평균값은 0이므로 사라진다.

시그마 제곱 - 원래 데이터를 생성하는 모델에 포함되어 있는 노이즈의 분산
Varience - 파라미터를 완벽하게 예측할 수 없기 때문에 생기는 오차
bias - 단순화하였기 때문에 생긴 오차
Variance와 bias를 동시에 줄여야한 전체 오차 값이 감소하므로 예측의 가장 큰 두 원인이다.
4차시 - 학습곡선
Learning Curves - 얼마나 학습했는지 확인, 언더 오버 피팅 진단, 성능 향상 시각화
Data가 증가함에 따라 Train error는 증가하고, Validation error는 감소하다가 일정 값 이상이 되면 수렴한다.
Train data를 늘려도 영향을 주지 못한다면 복잡도를 늘린다.
정규화 파라미터가 너무 작으면 데이터가 늘어나도 Validation과 Train오차가 크다. data를 많이 수집해야함
High Bias - 데이터 개수를 증가시켜도 언더피팅이 해결되지 않는다. train error만 늘어난다.
High Variance - 데이터 개수를 증가시키면 차차 줄어든다.
5차시 - 학습 알고리즘의 성능 향상
선형 회귀 함수를 만들어서 학습시키고 새로운 데이터에 적용했을 때 결과 예측에 매우 큰 오차가 발생!
1. train data 늘리기
High Variance 문제를 해결할 수 있지만 High bias문제는 해결할 수 없다.
Train error와 Validation error의 차이를 줄일 수 있다.
2. feature 수 줄이기
High variance 문제를 해결할 수 있다. 오버피팅 문제에 효과가 있다.
3. feature 수 늘리기
High-bias 문제 해결 가능하다.
train set에 더 적합해진다.
4. 다항식 늘리기
High bias 문제 해결 가능
feature를 추가하는 다른 방법이다.
5. 정규화 줄이기
high-bias 문제 해결 가능
6. 정규화 늘리기
high-variance 문제 해결 가능
작은 뉴럴넷은 계산량 면에서는 유리하지만 언더 피팅이 발생할 가능성이 존재한다.
큰 뉴렬넷은 오버피팅에 유의해야 하고, 정규화를 써야한다.
한개의 레이어에 많은 뉴런을 사용해보고, 해결되지 않으면 많은 레이어에 적은 뉴런을 사용해 본다.
10주 차
1차시 - 머신러닝 시스템 설계 시 고려사항
불균형 데이터에서 정확도는 머신러닝 알고리즘의 성능을 제대로 평가할 수 없다!
스팸 분류기 -> classification을 통해 분류할 수 있다.
단어 100개를 feature로 설정하여 있으면 1, 없으면 0으로 해서 input으로 넣는다. == feature은 100차원
데이터 수집은 가짜 이메일을 만들어서 여기저기에 뿌린다.
메일 헤더를 통해 스팸 메일인지 아닌지 알 수 있다. - 스팸 보내는 사람들은 이걸 속이기도 한다.
컴퓨터가 매칭할 수 없도록 이상하게 작성한 단어를 찾아내는 알고리즘도 만들어야 한다.
2차시 - 오차 분석 방법
머신러닝 구현시 단순한 알고리즘으로 구현하여 test와 validation, Learning curve를 통해 오버피팅, 언더피팅을 확인한다.
스팸 분류기에선 분류하지 못한 스팸 메일을 분석하여 그 부분에 대해 강화할 수 있다.
오차의 세부 내역을 보고 결정하는 것이다. - 성능 향상 방법을 위해 다양한 아이디어를 적용하고 성능 평가 가능
수치 평가 척도를 이용하여 성능이 얼마나 좋아졌는지 확인할 수 있다.
3차시 - 불균형 데이터의 경우 오차 평가 척도
불균형 데이터는 데이터의 수가 크게 차이가 나는 것으로 일반적인 정확도로 평가한다고 하면 대충해도 좋은 성능이 나오게 된다. == 불합리한 결과, 극단적인 경우 Skewed Classes
또한 정확도가 올라 갔다고 해도 성능이 좋아졌다고 하기 어려우므로 다른 척도가 필요하다.

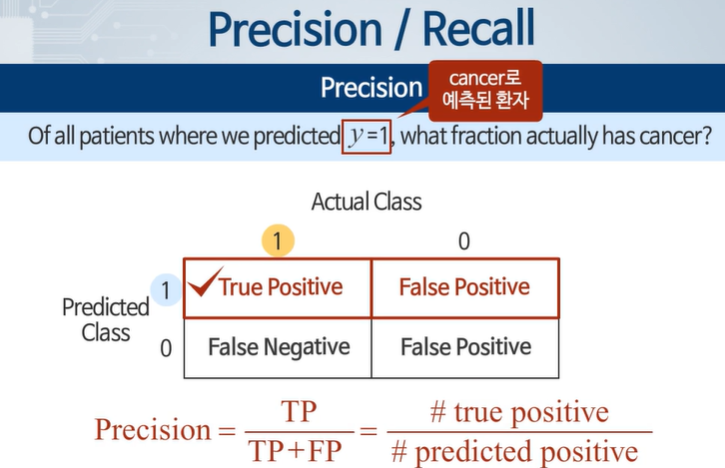
Postive로 예측한 사람들 중에서 실제 cancer 환자가 얼마나 되는가?

진짜 부정 중 예측을 부정으로 한 경우

4차시 - 정밀도와 재현율의 Trade-off
예측값이 0.7보다 높은 값이 나와야 Cancer로 예측하겠다 == high confident - Threshold가 크다.
Precision은 올라가고 Recall은 내려간다.
예측값이 0.3보다 높은 값을 Cancer라고 예측하겠다 == avoid false negative - Threshold가 작다.
진단 결과에서 암 환자를 놓치는 일 감소
Precision은 내려가고 Recall은 올라간다.
두 지표의 평가는 평균으로 하지 않고, f1 score를 사용한다.
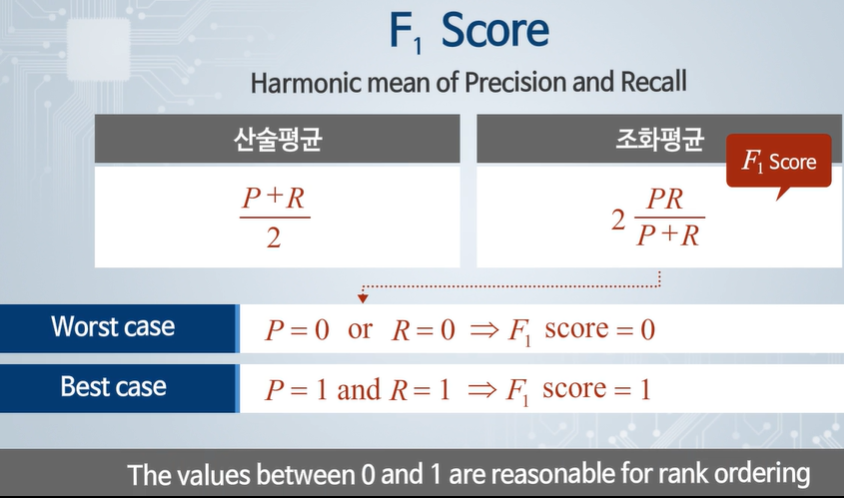
5차시 - 학습 데이터 수와 테스트 오차의 관계
충분한 특징 값과 parameter의 개수가 되어야 데이터가 늘어나도 쓸모가 있다. - Low Bias Algorithms
충분한 피쳐와 히든 레이어 수가 중요하다.
데이터가 부족하게 되면 High Bias Problem이 된다.
데이터 개수를 충분히 확보한다면 매우 높은 성능의 learning 아록리즘을 만들 수 있다.
11주 차
1차시 - SVM의 최적화

복잡하고 귀찮은 Logisitic Regression 문제를 직선함수로 근사화 시켜서 계산량도 훨씬 적다.

C가 잘못되는 경우 데이터에 매우 민감하다.
C는 정규화 항에서 나왔다. m도 없애준다.
이 비용함수를 최소화하기 위해 학습한다.
2차시 - 최대 마진 개념



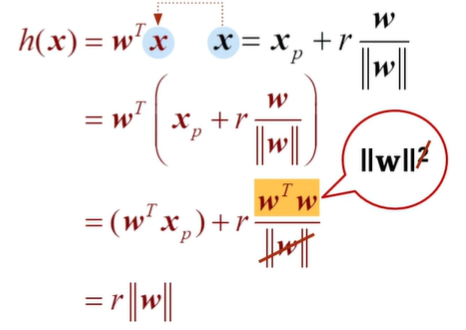
여기서 같은 w가 아닐텐데 왜 약분이 되고, 제곱이 되는거지 했는데, SVM 파라미터는 항상 decision boundary와 수직이라네요...?
네, SVM의 파라미터 ( w )는 항상 결정 경계(decision boundary)와 수직입니다. 이를 좀 더 자세히 설명해보겠습니다.
결정 경계와 파라미터 벡터 ( w )의 관계
- 결정 경계의 정의:
- 결정 경계는 ( w^T x + b = 0 )의 형태로 표현됩니다. 여기서 ( b )는 편향(bias) 또는 절편(intercept)입니다.
- 벡터 ( w )의 역할:
- 벡터 ( w )는 결정 경계의 법선 벡터(normal vector)입니다. 이는 ( w )가 결정 경계에 수직임을 의미합니다.
법선 벡터의 의미
- 법선 벡터:
- 법선 벡터는 주어진 평면이나 초평면에 수직인 벡터입니다. SVM의 경우, ( w )는 결정 경계 평면에 수직입니다.
- 즉, ( w )는 결정 경계와 직교하는 방향을 나타냅니다.
예시로 설명
- ( w = [w_1, w_2, \dots, w_n] )라고 할 때, 이 벡터는 ( x = [x_1, x_2, \dots, x_n] )와 내적(inner product)하여 ( w^T x ) 값을 계산합니다.
- 이 내적 값이 0이 되는 점들이 결정 경계를 형성합니다. 다시 말해, ( w^T x = 0 )인 점들이 결정 경계 위에 위치하게 됩니다.
- 벡터 ( w )는 이러한 점들에 수직이므로, ( w )는 결정 경계에 직각을 이루며 결정 경계의 법선 벡터로 작용합니다.
왜 수직인 것이 중요한가
- 최대 마진(maximum margin):
- SVM의 목적은 결정 경계에서 가장 가까운 데이터 포인트들까지의 거리를 최대화하는 것입니다. 이를 위해 결정 경계는 데이터 포인트들과 최대한 멀리 떨어지도록 위치합니다.
- 법선 벡터 ( w )는 이러한 마진을 정의하는데 핵심적인 역할을 합니다. ( w )의 방향은 결정 경계에서 가장 가까운 데이터 포인트로의 수직 방향을 나타내며, 이를 통해 마진의 폭을 조절합니다.
따라서 SVM에서의 파라미터 ( w )는 결정 경계와 항상 수직이며, 이는 SVM이 데이터를 분류하는 데 중요한 특성입니다.
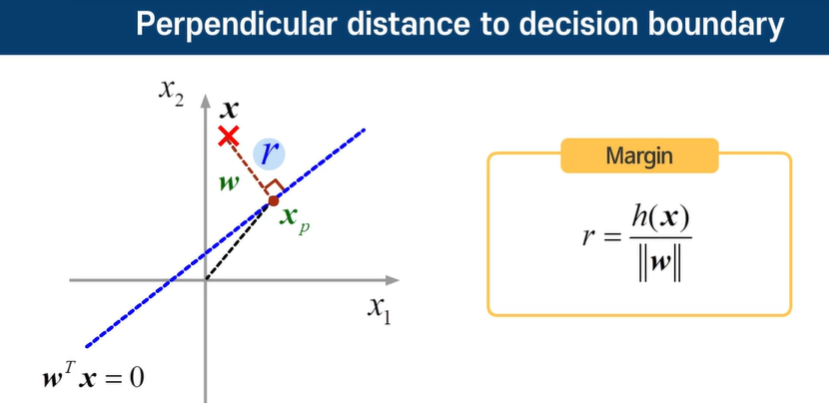

w 값을 극대화 해야 한다.
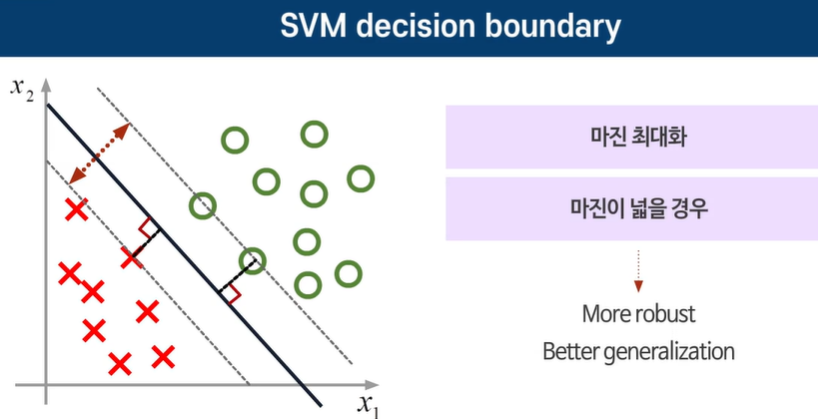
마진을 최대로 할 경우 일반화된다. == SVM
잘 못할경우 새로운 데이터가 나타났을 때 제대로 분류지 못한다. -> 마진이 작다.
이론적으로 많은 경꼐를 구할 수 있지만 최대 마진은 하나만 존재한다.
C가 큰 경우 람다가 매우 작으므로 잘못된 데이터에 매우 민감하다.
C가 작은 경우 람다가 커서 이상치에 약간의 영향은 받지만 강건한 분류선을 만든다.
마진 내부의 점들을 suport vector라고 부른다.
3차시 - 최대 마진 분류의 수학적 개념
내적에서 교환 법칙이 성립한다.
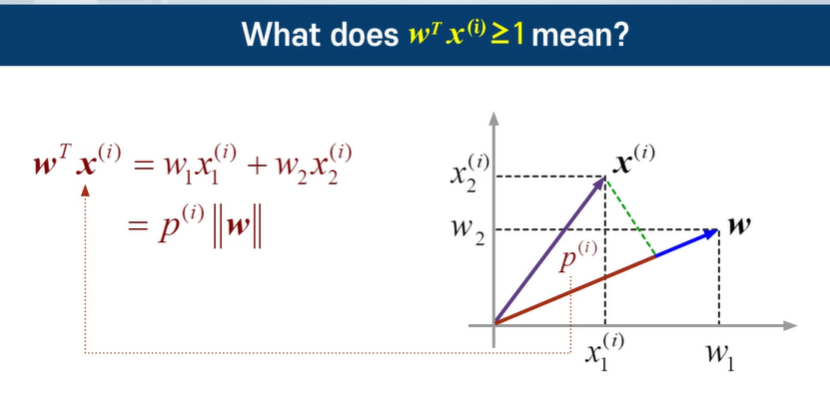
p의 길이는 projection의 길이이다.
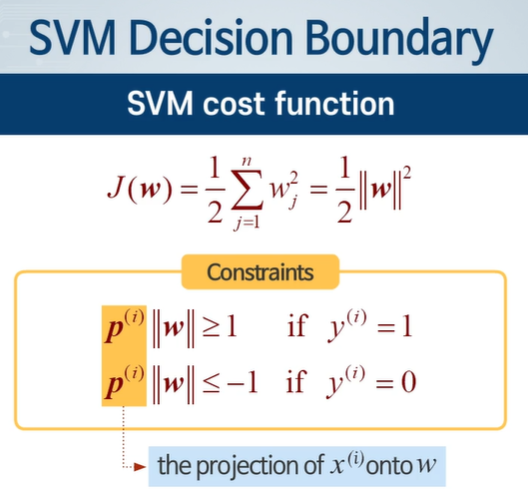
비용함수를 최소화 하려면 w가 작아야 하고, 조건을 만족하려면 w가 커야된다. -> P를 키워서 w를 작아도 되게 만들자.
데이터로부터 Projection시킨 p가 너무 작다면 즉 마진이 너무 작으면 w가 커져야 되므로 안된다.
P가 커져야 된다. Decision boundary와 수직인 Weight vector에 Projection시켰을 때 커야된다.
즉 SVM Decision Boundary는 마진을 최대화하는 방향으로 최적화 되었다.
4차시 - 커널의 개념
SVM에서는 다항식의 개념을 fi 라는 특징 값을 사용하여 고차 다항식 형태의 예측 함수를 만들어낼 수 있다.

다항식은 계산량이 많다는 문제가 있으므로 다항식 형태의 특징 값들을 사용하는 대신 더 좋은 다른 방법을 찾아내는 것이 필요하다.
커널 == 유사도

특정 위치에 설정하고, 가까워지면 1, 멀어지면 0을 둔다. 가우시안 분포를 활용해 가까워진 것과 멀어짐을 판단한다.
분산이 커지면 넓어지고, 작아지면 좁아진다.

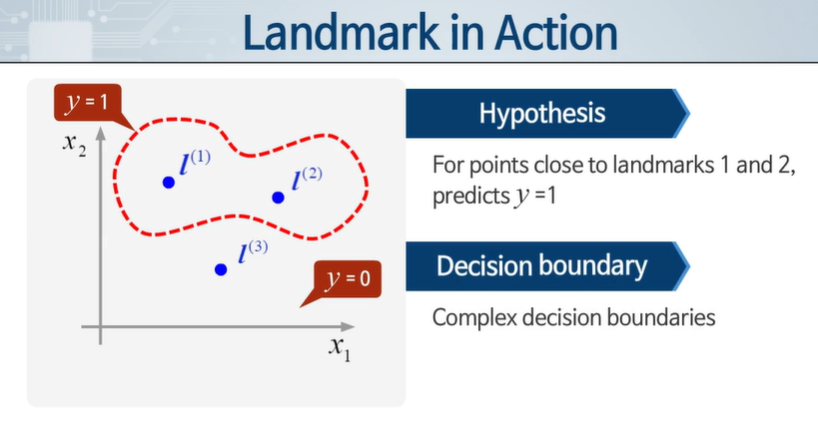
이를 통해 복잡한 decision boundary를 만들 수 있다.
그럼 저 l(랜드마크)은 어떻게 정할까?
학습 데이터와 동일한 위치에 랜드마크를 넣는다. == m은 데이터 개수
이 때 f 는 vias까지 m+1 차원이 된다.
여기서 자기 자신의 유사도는 전부 1이 되게 된다.

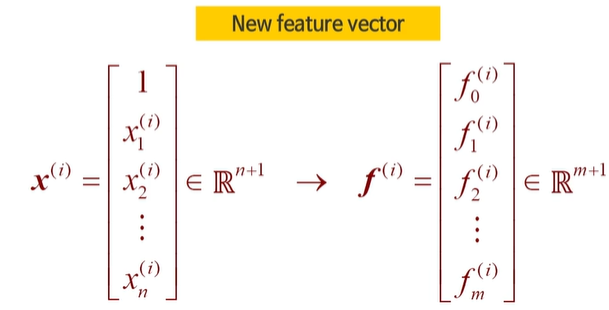
C가 크면 오버피팅
C가 작으면 언더피팅
시그마에 의한 폭이 조절이 되므로 커지면 스무스하게 된다. -> 언더피팅
시그마 폭이 작다 - 오버피팅
5차시 - SVM 적용하기
언더 피팅과 오버 피팅을 피할 수 있도록 C와 커널을 적절하게 잘 고른다.
커널을 사용할 때 스케일링이 필수적이다. 큰 값에 지배되기 쉬우므로 유사하게 만들자.
다중 분류 문제에서도 사용 가능하다. 1 vs all - 이진 분류하는 SVM 여러 개 만들기
n - num of features, m - num of example
n>> m ==> logistic regression을 사용한다. SVM을 커널 없이 사용한다. or 리니어 커널
n도 작고, m도 작다 ==> SVM 가우시안 커널로 사용한다.
n 작고, m이 큰 경우 - 가우시안 커널은 너무 오래걸려서 feature를 늘리거나 logistic regression, SVM 커널 없이
Logistic regression은 커널 없는 SVM과 유사하다.
DNN은 학습하고 연산하는데 시간이 오래 걸린다.
12주 차 - 클러스터링
1차시 - 비지도학습
라벨링 되어있지 않는 데이터로부터 패턴 등의 유용한 정보를 추출하는 것
유사한 데이터를 그룹핑하여 판매 전략, 패턴을 찾아낼 수 있고 특이 데이터를 찾아낼 수 있다.
데이터 특성에 기반해서 찾아내고, 라벨링하여 찾아낼 수 있다.
2차시 - K means 알고리즘의 원리
2가지 스탭을 반복적으로 진행한다.
1. 클러스터 할당 - 데이터들을 가장 가까운 클러스터 centroids에 포함되게 한다.
2. 클러스터 중심 업데이트 - 포함된 데이터들의 중앙으로 centroid가 이동한다.
Centroid의 좌표가 변하지 않으면 끝이다.
데이터가 작아진다 - 데이터가 서로 비슷해진다 == 유사도가 올라간다.
클러스터가 아무런 포인트도 포함하지 않으면 centroid 수를 줄이거나 새로 시작한다.
centroid는 정해져있거나 계속 시도해보면서 정한다.
3차시 - K means 알고리즘의 최적화 목적 함수
cost function == distortion : 가장 가까운 클러스터와의 mse
결국 2차시에서 했던 과정과 동일한 과정이다.

4차시 - 랜덤 호기화와 kMeans 알고리즘
랜덤이기 때문에 원하는 될 수도 있지만 이상하게 갈 수 있다.
초기화에 따라 global optima가 될 수도, local optima가 될 수도 있다.
여러 번 시도한 뒤 비용함수가 가장 낮은 값을 선택하면 가장 이상적인 clustering 결과가 도출된다.
클러스터의 개수가 지나치게 많은 경우 큰 도움을 기대할 수 없다.
5차시 - 클러스터 수의 결정
애매모호하기 때문에 명확하게 하기 어렵다.
클러스터의 개수도 여러개 두고 다 해본 다음 비용함수가 제일 많이 줄어든 뒤 감소가 팍 사라진 곳을 고른다.

전략에 따른, 분포에 따른 클러스터의 수를 결정하면 된다.
즉 사람이 고르기, Elbow method, 목적에 따른 선택이 있다.
13주 차 - 차원 줄이기
1차시 - 차원 줄이기의 목적
높은 차원의 데이터를 낮은 차원 데이터로 바꾸는 것이 차원 줄이기이다.
데이터 압축 : 정보량의 큰 손실 없이 사이즈 축소, 학습 알고리즘 속도 향상
데이터 시각화 : 시각화 하기 어려운 높은 차원의 feature data를 2, 3차원으로 변환
데이터의 상관관계(Redundant)가 높아야 한다.
높은 차원의 데이터들을 낮은 차원에 Projection하여 높은 중복성을 제거한다.
차원을 낮추면 시각화가 가능해지는 것이지 특별한 의미를 생각하면 안된다.
2차시 - Princicpal Component Analysis
PCA : 높은 차원 데이터의 차원을 줄이기 위해 낮은 차원의 평면에 데이터를 Projection하는 것
선형 회귀가 아니다.
데이터로부터 직선에 도달하는 오차를 최소화하는 선, 평면을 찾는다.
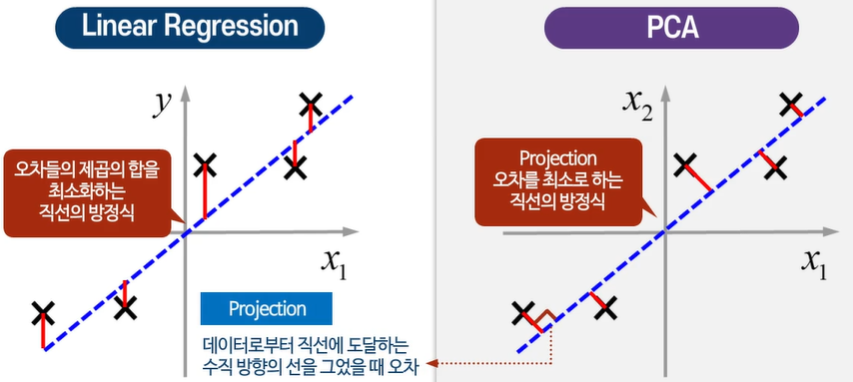
평균값 정규화 : 데이터를 평균으로 빼주어 평균을 0으로 만들기
여기선 투영시키는 거리가 작아야 좋은 Projection이다.
3차시 - PCA 알고리즘
전처리로 평균이 0으로 오게 만들어 준다. 그리고 feature 들이 비슷한 범위의 수치 값을 갖도록 스케일링 한다.

상관 행렬(정사각 행렬, 대칭 행렬)을 그리기 된다 - Transpose를 곱했다.



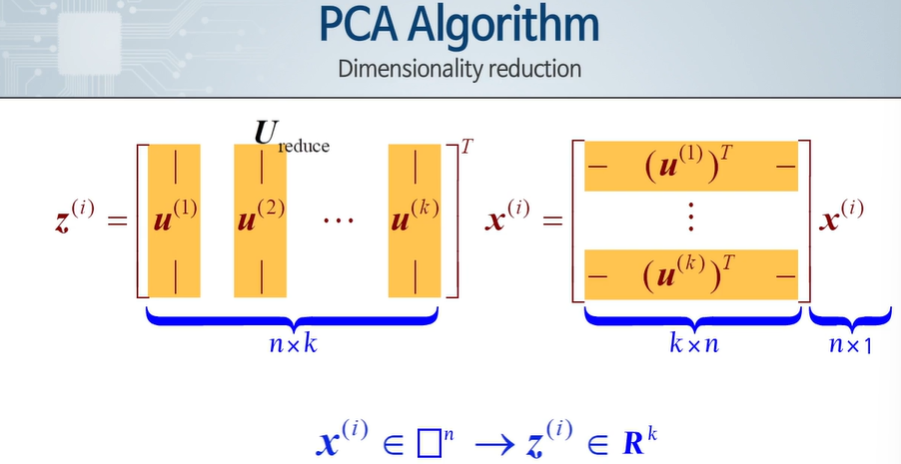
4차시 - Principal Component 수의 결정

가장 작은 값이 되는 k를 사용하여 평균 제곱 Projection 오차와 Total variation 비율을 고려하여 특정 조건을 만족하면 Principal Component 개수가 되는 것이다.

PCA(주성분 분석)에서 k를 구하는 알고리즘을 쉽게 설명해드리겠습니다. k는 주성분의 개수를 의미하며, 데이터의 차원을 줄이면서 중요한 정보(분산)을 최대한 유지하고자 할 때 설정하는 값입니다.
- 데이터 표준화: 먼저, 모든 데이터의 스케일을 동일하게 맞춥니다. 보통 각 변수의 평균을 0, 분산을 1로 표준화합니다.
- 공분산 행렬 계산: 표준화된 데이터의 공분산 행렬을 계산합니다. 공분산 행렬은 변수들 간의 상관관계를 나타냅니다.
- 고유값과 고유벡터 계산: 공분산 행렬의 고유값과 고유벡터를 계산합니다. 고유값은 각 주성분의 분산을 의미하며, 고유벡터는 주성분의 방향을 나타냅니다.
- 고유값 정렬: 고유값을 내림차순으로 정렬합니다. 큰 고유값일수록 더 많은 분산을 설명하는 주성분을 의미합니다.
- 고유값의 누적 합 계산: 고유값의 총합에 대해 각 고유값의 누적 합을 계산합니다. 이 누적 합을 통해 각 주성분이 데이터의 전체 분산에서 차지하는 비율을 알 수 있습니다.
- k 선택: 누적된 설명 분산 비율이 원하는 임계값(예: 95% 이상)을 넘는 최소한의 주성분 개수를 k로 선택합니다. 즉, 설명하고자 하는 분산의 비율을 설정하고, 그 비율을 넘기 위해 필요한 최소한의 주성분 개수를 결정합니다.
쉽게 말해, 데이터를 줄이면서도 최대한 원래의 정보(분산)를 유지하고자 할 때, 가장 중요한 정보(분산)를 설명할 수 있는 최소한의 주성분 개수를 선택하는 과정이 k를 구하는 알고리즘입니다.
예시
- 데이터를 표준화하고 공분산 행렬을 계산합니다.
- 공분산 행렬의 고유값이 5, 3, 1, 0.5, 0.2라고 가정해봅시다.
- 이 고유값들을 내림차순으로 정렬합니다: 5, 3, 1, 0.5, 0.2.
- 각 고유값의 누적 합을 계산합니다: 5, 8(5+3), 9(8+1), 9.5(9+0.5), 9.7(9.5+0.2).
- 총 고유값의 합은 9.7입니다.
- 각 주성분의 누적 설명 비율은: 5/9.7, 8/9.7, 9/9.7, 9.5/9.7, 9.7/9.7.
- 설명하고자 하는 분산의 비율을 95%로 설정한 경우, 누적 설명 비율이 95% 이상인 최소 주성분 개수를 찾습니다. 여기서는 세 번째 주성분까지 합한 값이 9/9.7로 약 92.8%입니다. 네 번째 주성분까지 합하면 약 97.9%로 95%를 넘습니다.
- 따라서 k=4로 선택할 수 있습니다.
물론입니다! 공분산 행렬 계산을 쉽게 설명해드릴게요.
공분산이란?
공분산은 두 변수 간의 관계를 나타내는 값입니다. 두 변수가 함께 어떻게 변하는지를 보여줍니다.
- 양의 공분산: 한 변수가 증가할 때 다른 변수도 증가하면 양의 공분산이 나옵니다.
- 음의 공분산: 한 변수가 증가할 때 다른 변수는 감소하면 음의 공분산이 나옵니다.
- 공분산이 0: 두 변수 간에 아무런 상관관계가 없으면 공분산이 0입니다.
공분산 행렬이란?
공분산 행렬은 여러 변수들 간의 공분산 값을 모아놓은 정사각형 행렬입니다. 예를 들어, 세 개의 변수가 있다면 공분산 행렬은 3x3 행렬이 됩니다.
공분산 행렬 계산 방법
- 데이터 준비: 표본 데이터가 여러 변수로 이루어져 있다고 가정합니다. 각 변수는 열로, 각 관측치는 행으로 표현됩니다. 예를 들어, (X)는 변수 1, 변수 2, 변수 3을 포함하는 데이터 행렬입니다.
- 평균 중심화: 각 변수의 평균을 계산하고, 각 관측치에서 해당 변수의 평균을 뺍니다. 이렇게 하면 각 변수의 평균이 0이 됩니다. 이를 중심화된 데이터 행렬이라고 합니다.
- 공분산 계산: 중심화된 데이터 행렬을 사용하여 공분산을 계산합니다. 두 변수 간의 공분산은 다음과 같이 계산됩니다.
- 공분산 행렬 구성: 위의 공분산 계산을 모든 변수 쌍에 대해 반복하여 공분산 행렬을 구성합니다. 행렬의 대각선 요소는 각 변수의 분산이고, 비대각선 요소는 변수 간의 공분산입니다.
이게 더 나은거 같네요
PCA에서 ( k ) 값을 구하는 방법에는 여러 가지 접근 방식이 있으며, 이미지에서 설명하는 방식도 유효한 방법 중 하나입니다. 이를 단계별로 설명하겠습니다.
이미지에서 설명하는 방식 (점진적 접근법)
- 초기 설정: ( k ) 값을 1로 설정합니다. ( k )는 주성분의 수를 나타냅니다.
- 계산:
- 데이터의 주성분을 이용해 차원을 ( k )로 줄입니다. 즉, ( k )개의 주성분을 사용하여 원래 데이터의 근사값을 계산합니다.
- 이를 통해 ( \mathbf{U}{\text{reduce}}, \mathbf{z}^{(1)}, \ldots, \mathbf{z}^{(k)}, \mathbf{x}{\text{approx}}^{(1)}, \ldots, \mathbf{x}_{\text{approx}}^{(m)} ) 값을 구합니다.
- 검사:
- 원래 데이터와 근사 데이터 간의 오차를 계산합니다.
- 다음 조건을 확인합니다:
[
\frac{1}{m} \sum_{i=1}^{m} \frac{| \mathbf{x}^{(i)} - \mathbf{x}_{\text{approx}}^{(i)} |^2}{| \mathbf{x}^{(i)} |^2} \leq 0.01
]
이는 데이터의 근사값이 원래 데이터와 얼마나 가까운지를 나타내는 비율입니다.
- 조건 충족 여부 확인:
- 조건이 충족되면 현재의 ( k ) 값을 선택합니다.
- 조건이 충족되지 않으면 ( k ) 값을 1 증가시키고, 다시 계산 단계로 돌아갑니다.
- 종료:
- 조건이 충족될 때까지 위 과정을 반복합니다.
- 조건이 충족되면 ( k ) 값을 최종적으로 결정하고 종료합니다.
요약
이 점진적 접근법은 ( k ) 값을 1부터 시작하여, 데이터를 잘 근사할 수 있을 때까지 ( k ) 값을 증가시키며 반복하는 방식입니다. 이는 조건을 만족할 때까지 반복적으로 계산하고 검사하는 과정이기 때문에 효율적이지 않을 수 있습니다.
하지만 이 방법은 원하는 근사 정확도를 명시적으로 설정하고 그에 맞추어 최적의 ( k ) 값을 찾을 수 있다는 장점이 있습니다.
비교
반면, 앞서 설명한 고유값 기반 접근법은 한 번의 계산으로 각 주성분이 설명하는 분산의 비율을 구하고, 이를 기반으로 ( k ) 값을 선택하는 방법입니다. 이 방법은 일반적으로 더 빠르고 효율적입니다.
따라서 두 방법 모두 유효하지만, 효율성 면에서 고유값 기반 접근법이 더 선호될 수 있습니다. 각각의 상황에 따라 적절한 방법을 선택하는 것이 중요합니다.
좋은 질문입니다. ( k = 1 )인 경우를 포함하여 ( k ) 값을 증가시키면서 원래 데이터와 근사 데이터 간의 비교가 어떻게 이루어지는지 좀 더 구체적으로 설명드리겠습니다.
( k = 1 )일 때의 경우
- 주성분 분석:
- PCA를 수행하면, 원래의 고차원 데이터가 주성분(Principal Component) 축으로 변환됩니다.
- ( k = 1 )인 경우, 첫 번째 주성분 축(가장 큰 분산을 설명하는 축) 하나만 사용합니다.
- 차원 축소 및 근사값 계산:
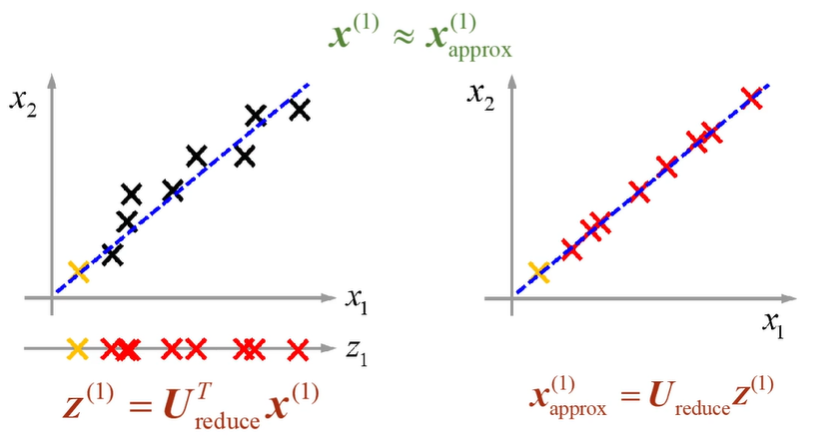
- 원래 데이터 ( \mathbf{X} )를 첫 번째 주성분 ( \mathbf{u}_1 )으로 투영하여, 새로운 값 ( \mathbf{z}_1 )을 얻습니다.
- 이 투영된 값을 다시 원래의 고차원 공간으로 변환하여 근사값 ( \mathbf{x}_{\text{approx}} )를 계산합니다.
- 예를 들어, 원래 데이터 (\mathbf{x}^{(i)})가 주어지면, 근사 데이터는 다음과 같이 계산됩니다:
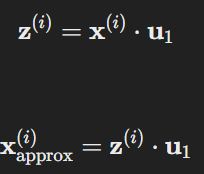
- 여기서 (\mathbf{u}_1)은 첫 번째 주성분 벡터이며, (\mathbf{z}^{(i)})는 (\mathbf{x}^{(i)})가 첫 번째 주성분 축으로 투영된 값입니다.
- 오차 계산:
- 원래 데이터 (\mathbf{x}^{(i)})와 근사 데이터 (\mathbf{x}_{\text{approx}}^{(i)}) 간의 오차를 계산합니다.
- 오차는 다음과 같이 계산됩니다:

- 여기서 ( | \cdot | )는 벡터의 노름(norm)을 나타냅니다.
예시
예를 들어, 두 변수 (즉, 2차원)로 이루어진 데이터가 있다고 가정해 봅시다:
- 원래 데이터:

- 주성분 분석 결과:
- 첫 번째 주성분 벡터가 (\mathbf{u}_1 = (0.6, 0.8))라고 가정합니다.
- 차원 축소 및 근사값 계산:
- 각 데이터 포인트를 첫 번째 주성분 축으로 투영합니다:

- 근사 데이터를 계산합니다:

- 각 데이터 포인트를 첫 번째 주성분 축으로 투영합니다:
- 오차 계산:
- 각 데이터 포인트의 오차를 계산합니다:
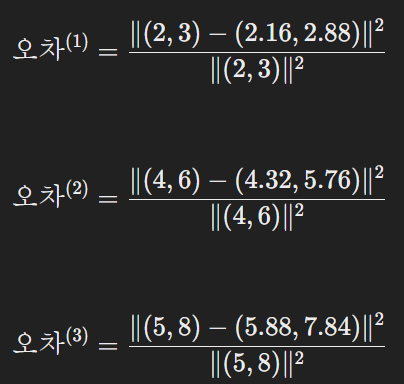
- 평균 오차를 계산하여 조건을 확인합니다:

- 각 데이터 포인트의 오차를 계산합니다:
위 과정에서 ( k = 1 )인 경우에도 원래 데이터와 근사 데이터를 비교할 수 있습니다. 각 데이터 포인트의 근사값은 첫 번째 주성분 축으로 투영된 후 다시 원래 공간으로 변환된 값이며, 이를 통해 원래 데이터와 근사 데이터 간의 차이를 계산할 수 있습니다. 이를 통해 원래 데이터가 얼마나 잘 보존되는지 평가할 수 있습니다.
동일 계산을 너무 반복해야 한다. -> S를 사용하여 효율적으로 하자.




5차시 - PCA 적용 방법
입력 데이터가 이미지라면 차원이 커져서 계산량이 엄청 는다.
PCA를 통해 압축시킬거면 test data 또한 같이 압축해야한다.
PCA를 오버피팅 해소용으로 사용하면 잘못된 것 이다.
대신 정규화를 사용해라
PCA를 사용하지 말고 원래 데이터를 사용하다가 만족스럽지 않으면 사용해라
PCA도 시간이 걸리는 작업이고, 오차도 나올 수 밖에 없기 때문이다.
14주 차 - 이상 데이터 검출
1차시 - 이상 데이터 검출 문제 정의
일반적으로 발생하지 않는 정상적이지 않은 데이터는 이상 데이터이다.
feature로 열, 진동, 강도 등 다양하게 사용할 수 있고, 정상 범위에서 많이 벗어난다.
2차시 - 가우시안 분포
가우시안 확률분포는 정규분포로 평균과 분산으로 이루어져있다.

전체 면적은 1로 분산이 퍼짐을 결정한다.
평균과 표준편차는 데이터의 평균값을 찾아서 근사화할 수 있다.
m(데이터 수)가 충분히 클 경우 m-1과 m은 거의 유사하다 == Estimate가 유사하다.
m이 작은 경우 m과 m-1은 차이가 있다 == Estimate간 차이가 존재한다.
3차시 - 이상 데이터 검출 알고리즘
모두 독립이라고하면 모든 확률 분포를 곱해서 확률을 나타낼 수 있다.

저것이 일정 크기보다 크다 작다로 0,1로 나눌 수 있다.
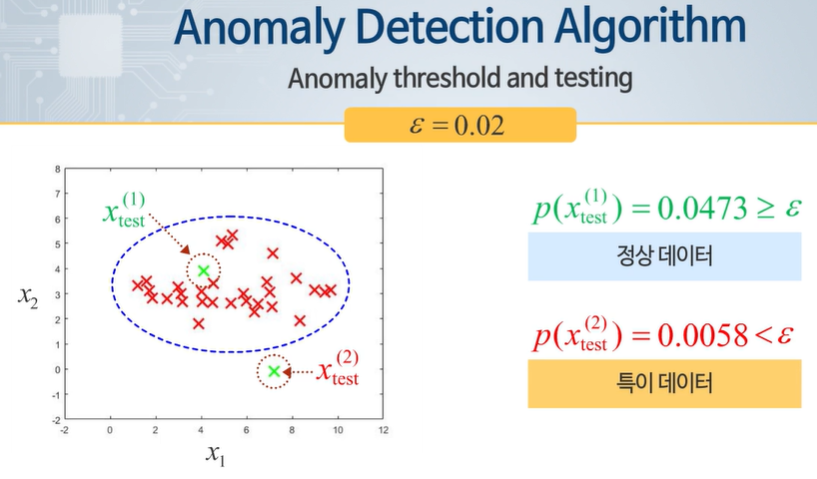
정상 데이터만 학습에 활용하고, 이상 데이터는 test와 validation에서만 활용한다.
평가할 때 정확도 말고 Precision, Recall, F1score 등 다양한 지표를 사용하여 정해야 한다.
4차시 - 이상 데이터 검출을 위한 특징 변환
불균형 데이터는 타입에 따라 데이터 수의 차이가 있어서 학습하기 매우 힘들다.
Transform - feature의 분포를 가우시안 분포로 변형한다.
어떤 함수를 사용할지는 잘 판단해야 한다.
비정상 데이터지만 정상 데이터 분포 안에 들어가 있다 -> 차원 수를 늘려서 효과적으로 Anomaly detection을 진행한다.
feature를 선택할 때는 이상 데이터가 발생했을 때 크게 변하는 값을 선택하고, 그 값들을 통해 새로운 feature를 만들 수 있다.
5차시 - 다변수 가우시안 분포
정상적인 데이터는 선형적인 분포, 가우시안 분포를 가진다.
적은 차원에서 보면 특이하다고 보기 힘들 경우도 있다.
이상 데이터가 기울어진 분포를 확인했을 때 이상데이터임을 확인할 수 있는 경우가 있으므로 다변수 가우시안을 잘 확인해야 한다. - Multivariate Guassian distribution
각 특징 값은 가우시안 확률 분포를 가지지만 확률적으로 독립이란 가정을 뺀다.


시그마의 변화를 통해 가우시안 분포의 분포 변화와 같은 효과를 낼 수 있다.
평균에 따라 이동도 한다.
다변수 가우시안을 통해 일반적이고 이상 데이터를 찾아내기 어려운 경우에도 적용 가능하고, 독립이라고 가정할 경우도 특이 데이터를 도출 가능하다.

항상 데이터 개수가 특징 개수보다 커야한다.
'인공지능 > 공부' 카테고리의 다른 글
| 생성형 인공지능 입문 1~5주 차 정리, 퀴즈 (2) | 2024.06.11 |
|---|---|
| 모두를 위한 머신러닝 기말고사 (0) | 2024.06.10 |
| 모두를 위한 머신러닝 1 ~ 7주차 정리 (0) | 2024.06.09 |
| 모두를 위한 머신러닝 기말 문제 풀기 (0) | 2024.06.09 |
| 생성형 인공지능 입문 - 14주차 퀴즈 (1) | 2024.06.03 |