공대생 도전 일지

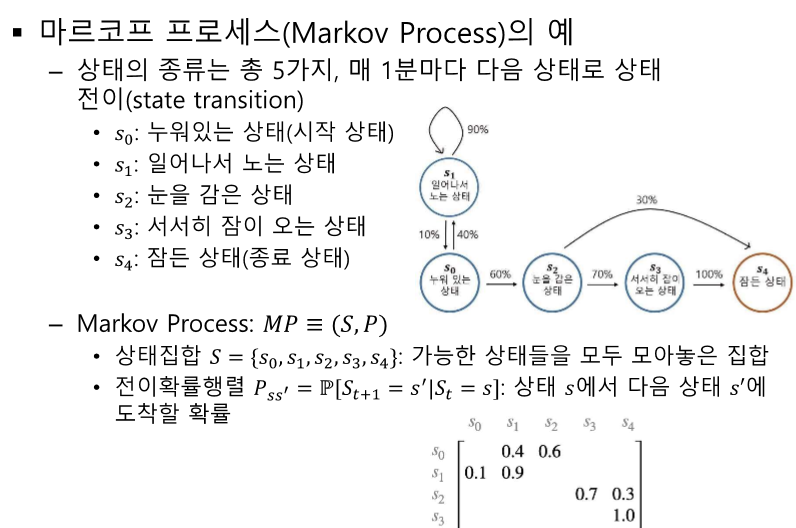
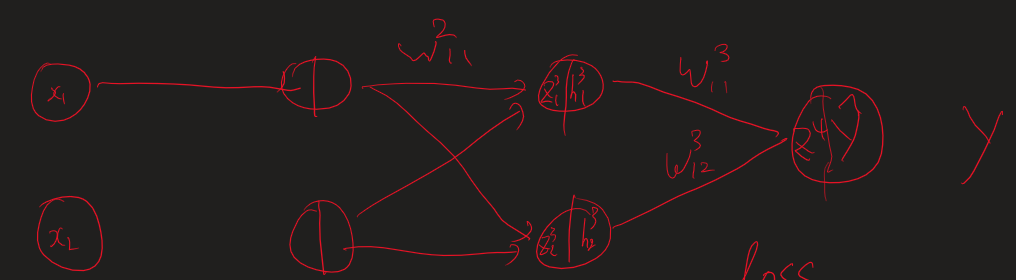
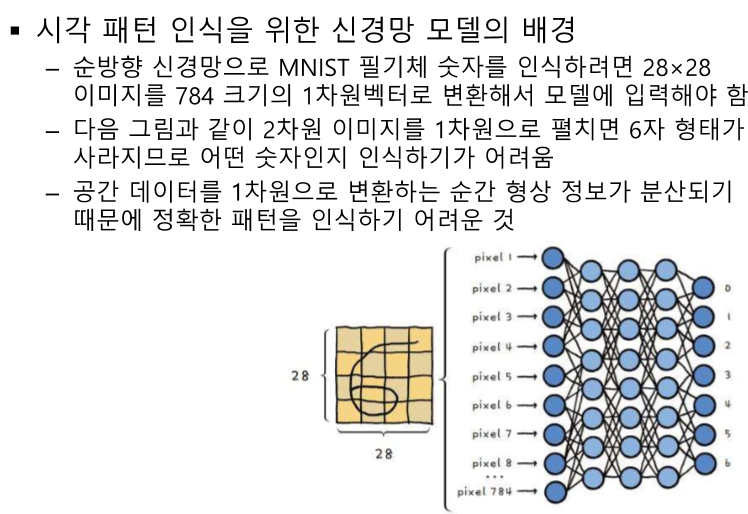
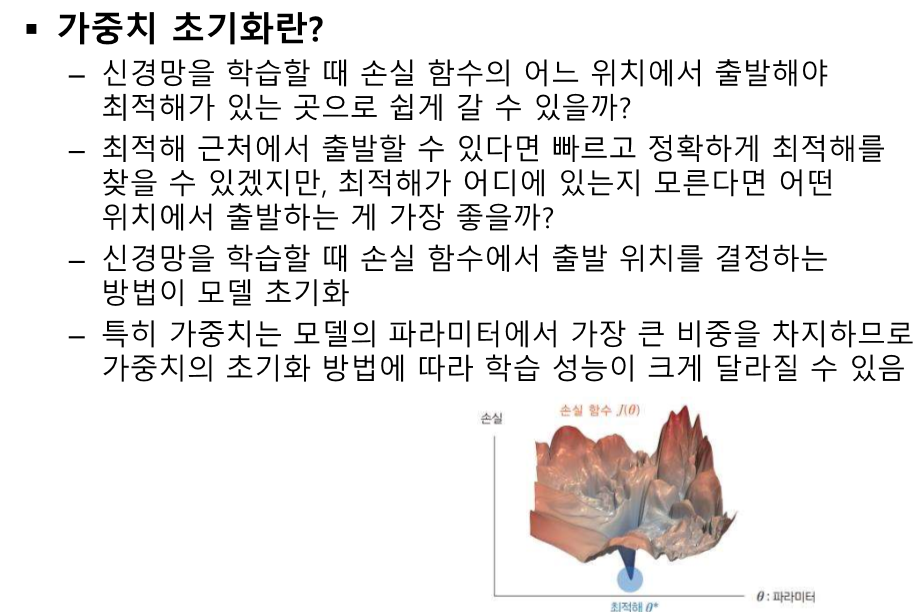
R- 보상, 리워드 G - 리턴 v - 상태 가치 방정식 q - 액션 가치 방정식 E - 평균 취하기 * - 최적 값 t - 상태 시간 단위 (k 보다 작은 시간인데 이전에서 나왔던 시간의 개념과 똑같다.) k - 에피소드 시간 단위 평균은 어디? - 어차피 마지막에 평균있어서 ㄱㅊ 항상 성립하는 것은 아니다 v(s) != v(s')이기 때문 v : s에 대한 리턴의 기댓값 액션이 추가되었다. v(특정 s의 가치)와 q(특정 s에서 a를 취했을 때 가치)의 관계 모델 프리 : 결과는 얻어지나 어떤 값으로 계산되는지 모르는 경우 v와 q의 선택은 목표에 따라 다르다. 어떤 위치에 도달해야 한다. S를 변화해야 한다. S를 예측할 수 없다. -> q를 사용한다. s'을 모를 때 q(s,a)를 대신해서 사용한..

지도 학습 - 정답 비지도 학습 - 목적 함수 강화 학습 - 보상의 총합 최대화 -> 보상이 학습을 가능하게 해준다. 누적합 - 시간의 흐름에 따라 보상이 쌓인다. 끝나면 그게 하나의 에피소드이다. 에이전트 - 게이머, 사람 환경 전체를 이해하고 모델링 할 수 있다. -> 굳이 강화학습 사용하지 않아도 된다. 환경이 너무 복잡해서 일부만 쓴다. -> state, 간소화해서 모델링 한다.

모든 상태를 행렬로 포함한다. - 행별로 쭉 더해서 1이 되는지 확인 확률로 정의하는데 t 이전의 과거는 필요없다! -> 메모리 감소 효과도 있다. 체인 룰에 의해서 다음을 계속 예측할 수 있다. 모든 상황이 마르코프 상태가 맞는 것은 아니라 정답이 아닐 수 있다. 그러나 모델링은 가능하다! 자율주행에서의 현재 상태 == 한 장만으로는 판단할 수 없다. - 10초간의 여러 사진을 하나로 볼 수 있다. 감쇠인자를 통해 미래 보상의 불확실성을 표현할 수 있따. 리턴의 정의 : 특정 시점, 상태에서의 리워드 합 G: 리턴, R: 보상, S: 상태 리턴(G)가 과도하게 커지면 프로그램의 숫자 표현형을 넘길 수 있고, 게임이 안 끝날 수 있다. 가치(V) != 리워드(R)! 내가 미래에 무엇을 받을 지 모르니 기..

생성형 인공지능 - 어마어마하게 많은 GPU가 필요하다. 달리나 chat GPT - 몇 만개의 GPU사용 ? 다양한 생성 AI가 있다 - 비디오, 텍스트, 사진, 음악 등 자율 주행, 로봇, 드론 등 모든게 AI로 진행되고 있다. ...? 들어오는 것 인식 -> Encorder에서 담당한다. (얼굴 인식 등 Convolution도 인코더와 비슷한 느낌이다) Decorder - 발생 - GPT도 디코더 모델! 컴퓨터 vision(영상처리)의 발전 - 자연어 처리에서 나왔다. Transformer? RNN? 토큰화화 후 자연어를 컴퓨터가 인식할 수 있는 embedding 벡터로 변환 embedding - LSTM과 RNN이 했었다. 길면 죽어! Transformer - 길어도 상관없다. 행렬의 크기만 하드웨..

단순하게 이렇게 이어진 네트워크가 있다고 가정하겠습니다. 입력은 x, 가중치와 곱해진 값들은 z, activation함수를 통과하면 h, 출력값은 y_hat입니다. 일단 이 경우에는 loss function으로 binary Cross entropy와 MSE를 사용하는 2가지 경우로 볼 수 있죠 그럼 가장 가까운 가중치인 3번째 layer의 첫번째 node에서 나오는 weight를 업데이트 해봅시다. 일단 loss function을 미분해야죠 벌써 지저분.. 그리고 Prediction y (y hat)를 미분합니다. 이것은 z값에 sigmoid를 씌운 값으로 sigmoid 미분을 진행합니다. sigmoid 미분은 하려고하면 귀찮지만 외우면 단순합니다.. 그럼 이제 마지막으로 파라미터로 미분을 때려주면 이전..

2차원 공간상의 위치정보를 고려해야하는 data에 대해서 효과적으로 사용된다. 단순한 계산 과정을 보여준다. 서브 샘플링 - 데이터 수를 줄인다. 풀링은 모든 layer에 사용하는 것은 아니고 필요할 때 적절하게 사용한다. 패딩을 할 순 있지만 안 할뿐 배치 정규화가 생각보다 시간 많이 사용하니까 적당히 쓰기 겅중 겅중 뛰어 다니는 것 입 출력 사이즈 조절 및 가장 자리 feature의 인식률 Up 입력 사이즈가 필터를 거칠수록 작아진다 -> 패딩으로 막는다. 사이즈가 유지된다. 수용 영역이 넓어진다. -> 깊이의 한계가 생긴다. weight 수가 확 줄었다. == 학습시켜야 할 파라미터가 줄었다. But filter 수가 늘면 파라미터가 는다. 위치가 어디있든 feature는 똑같이 추출된다. 1. 파..

초기 값이 얼마인지에 따라 결과가 천차 만별이다. 편향성을 주게 된다. 너무 작은 값으로 계속 곱하면 0에 모이게 된다. 비슷하다 -> 구분이 안간다 -> 예측에 활용될 수 없다. 가중합을 하면서 수가 엄청 커진다. 이것도 중앙으로 모여야 하는데 양 끝으로 값이 벌어진다. 계층을 통과할 때 마다 음수가 날라간다. overfitting == 일반화 오류가 크다. 오리지널의 라벨을 가지고 가는데 6이 너무 회전하면 헷갈리니까 한계를 정해야 한다. 독립 -> 편향제거 다 다른 모델을 넣어도 되고, 모양이 같은 모델을 넣어도 된다. 같은 데이터 -> 입력 데이터를 독립적으로 독립성이 중요하다 드롭아웃은 통상적으로 20퍼 사용한다. 네트워크 초반 - 일반화를 위해 출력단 - 소프트 레이블링

아담, 모멘텀 그런 류들 잔뜩 나오겠네요 그냥 이런 것이 있다 정도.. 분모가 계속 커진다. -> 0에 수렴한다. 분자에도 만들어 0으로 가는 것을 막자! 굳이 분자 문모 다 만들지 말고 0만 안되게 하자 기울기 대신에 기울기를 누적한 것을 더해준다. 논리 게이트 구현 1 논리 게이트 구현 2 정규화의 중요성!

이미지에서 설명하는 내용은 이항 분류(binomial classification) 문제에서의 클래스 결정 방식과 클래스 확률을 계산하는 과정을 나타냅니다. 주어진 입력 ( X )에 대해 두 클래스 ( Y_1 )과 ( Y_2 ) 중 어느 쪽에 속하는지 결정하는 과정이며, 확률적 관점에서 접근합니다. 확률 ( P(Y_1|X) )는 입력 ( X )가 주어졌을 때 클래스 ( Y_1 )에 속할 조건부 확률입니다. 이는 베이즈 정리를 사용하여 다음과 같이 계산할 수 있습니다: [ P(Y_1|X) = \frac{P(X|Y_1)P(Y_1)}{P(X)} ] 여기서 ( P(X|Y_1) )은 클래스 ( Y_1 )이 주어졌을 때 입력 ( X )가 관측될 확률이고, ( P(Y_1) )은 클래스 ( Y_1 )의 사전 확률입니다...

XOR은 단층 신경망으론 절대로 못 만든다... 비선형성을 추가해주는 activation function! 영향력을 조절한다... 좋네요 x0 = 1 w0= bias다. sigmoid보다는 도함수가 조금 더 크다. 이건 둘중 하나만 구분할 때 사용한다. 마지막 레이어의 노드가 하나만 있어야 한다. 사진과 같은 경우에는 모든 픽셀을 다 맞출 필요가 없다 즉 loss function의 구조를 다시 만든다 ex) cos 유사도