
모든 상태를 행렬로 포함한다. - 행별로 쭉 더해서 1이 되는지 확인

확률로 정의하는데 t 이전의 과거는 필요없다! -> 메모리 감소 효과도 있다.
체인 룰에 의해서 다음을 계속 예측할 수 있다.
모든 상황이 마르코프 상태가 맞는 것은 아니라 정답이 아닐 수 있다.
그러나 모델링은 가능하다!

자율주행에서의 현재 상태 == 한 장만으로는 판단할 수 없다. - 10초간의 여러 사진을 하나로 볼 수 있다.

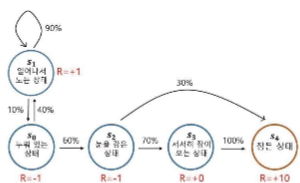

감쇠인자를 통해 미래 보상의 불확실성을 표현할 수 있따.
리턴의 정의 : 특정 시점, 상태에서의 리워드 합
G: 리턴, R: 보상, S: 상태

리턴(G)가 과도하게 커지면 프로그램의 숫자 표현형을 넘길 수 있고, 게임이 안 끝날 수 있다.

가치(V) != 리워드(R)!
내가 미래에 무엇을 받을 지 모르니 기댓값을 사용하여 확률로만 알 수 있게 된다.

어떤 상태가 더 좋을지 판단 가능하다.
Gt가 한개가 아니기 때문(경우의 수가 많다.)에 평균을 한다.

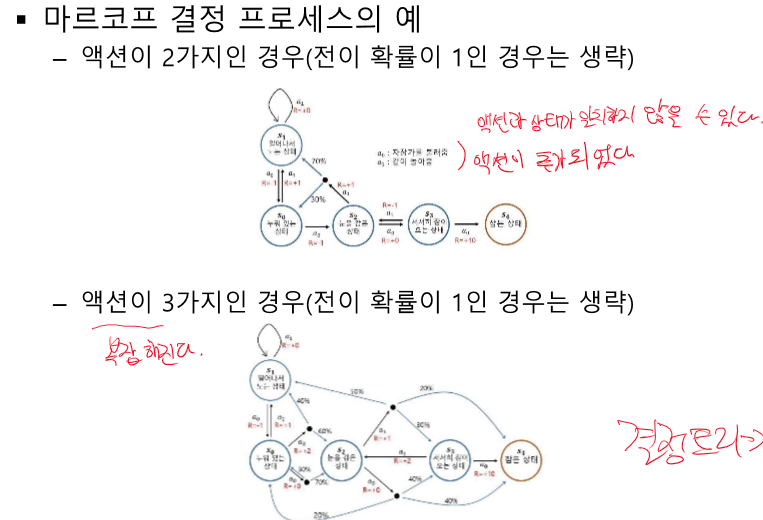

정책 함수 : 처음에는 모른다 -> 학습해야 한다. 어떤 액션을 취할지는 보상을 생각해서 구해야 한다.
상태 가시 함수 : 특정 정책에 따른 위치의 가치를 평가하여 높은 가치의 상태로 진행하려고 한다.
액션 가치 함수 : 액션은 결과를 보여주지 않는다. BUT우린 어떤 액션을 취해야 할지 찾는다.(정책) -> 최적의 액션의 나열 == 정책


Prediction - value를 구하는 과정, 한번에 못 구해도 여러번 반복한다.
Control - 최적의 정책을 찾는 과정
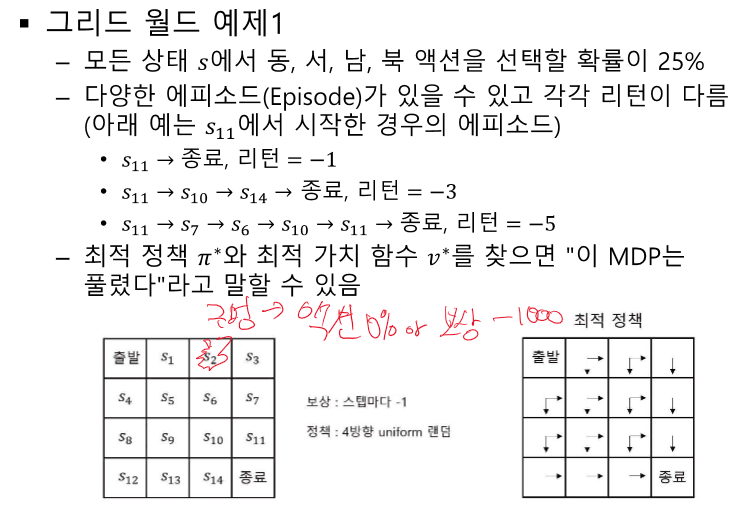
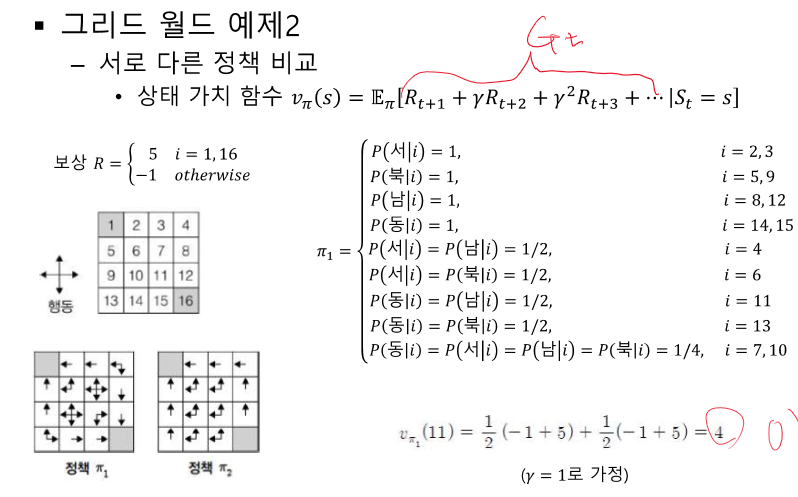
끝까지 가는 것은 연산이 너무 크다. V를 V로 계산한다.

'인공지능 > 공부' 카테고리의 다른 글
| 강화 학습 정리 - 3강 벨만 방정식 (1) | 2024.04.20 |
|---|---|
| 강화학습 정리 - 1강 강화학습이란? (0) | 2024.04.20 |
| 생성형 인공지능 특강 (0) | 2024.04.17 |
| Back propagation 손으로 하나하나 적어보기 (0) | 2024.04.17 |
| 딥러닝 개론 6강 - 합성곱 신경망 CNN 1 (0) | 2024.04.16 |