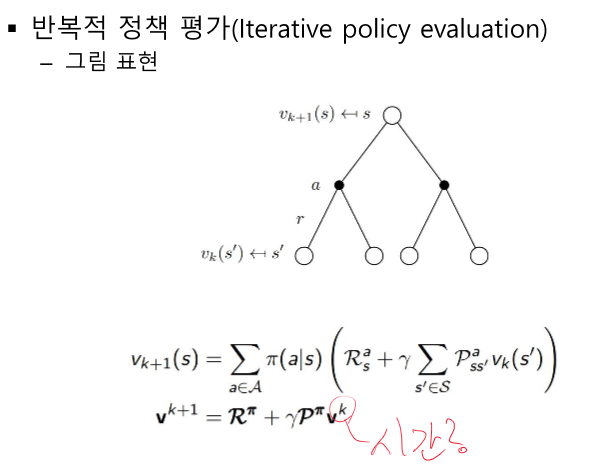
여기서 k는 에피소드 단위의 시간!
반복적 정책 평가 - 각 s에 대한 v 반복 계산 가능
벨만 기대 방정식을 이용해 업데이트를 계속해서 실제 가치를 알 수 있다.
업데이트할 때 k단위의 시간 잘 안보면 무너질 수 있다. ( 행렬을 두고 하나만 업데이트 해야 한다.)
정책 이터레이션 - 정책 평가(v구하기)와 정책 개선(정책 생성)의 반복 -> 수렴
그리디 정책 - 먼 미래를 생각하지 않고 다음 칸의 v가 가장 큰 것을 선택
v평가(정책 평가) -> 높은 v만 따라가는 정책 만들기(정책 개선) -> 다시 v평가 반복 ----> 수렴
정책 개선 보다는 평가하는데서 많은 연산 수행 -> 평가 간소화 하는 것 가능 (최적 정책 찾는게 목적)
-> 정책 평가를 1단계만 수행하고 정책 개선 - 빠른 정책 평가와 개선 가능 -> 최적 정책 빠른 찾기

최적 v를 알면 최적 정책을 얻을 수 있다.
모델 프리 - r과 P를 모르는 상황
MC 학습의 특성 - 확률을 몰라도 여러번 샘플링하여 가늠하는 기법 (대수의 법칙 가능)
v를 구할 때 실제 MDP를 모르더라도 s에서 여러번 G를 구한 후 평균 구해서 계산 가능
몬테 카를로 학습 - r과 P를 몰라도 N(방문 횟수) V(리턴의 총합 기록)을 통해 학습한다.
전부 경험(에피소드 종료 후) 후 역으로 계산하여 작성한다.

v 계산은 수 많은 에피소드 경험 후 V를 N으로 나눠서 사용한다. = 몬테카를로 방법론
알파(기존 값에 얼마나 변화를 줄 거냐)를 사용하여 조금씩 업데이트 하는 방법도 있다.
제한점 - 에피소드가 끝난 후에 업데이트 해야 한다 == 적용할 수 있는 환경이 제한적
-> 에피소드가 끝나기 전에 업데이트 하자!== TD

TD는 각각 s 변화가 일어나자 마자 테이블 값을 업데이트 한다.

Episodic MDP - 종료 상태가 있는 경우 -> MC, TD 모두 가능
Non - Episodic MDP - 종료 상태 없이 하나의 에피 소드가 무한히 이어지는 MDP -> TD만 가능
편향성 - bias : 어디에 치우치지 않았나 (잘못된 길로 빠질 수 있나)
MC - 가치 함수의 정의 : 여러 개의 샘플에 대한 평균을 구하기 때문에 편향이 적다
TD - 벨만 기대 방정식 : 바로바로 이전 값에 대해 업데이트 하기 때문에 편향이 크다.
분산 - Variance : 변동성이 큰가
MC - 에피소드가 끝나야만 하기 때문에 다양한 값 가질 수 있다. - 분산이 크다
TD - 한 샘플만 보기 때문에 분산이 작다.
n step TD



람다가 평균을 만드는 역할을 한다.

'인공지능 > 공부' 카테고리의 다른 글
| 딥러닝 개론 정리 7강 - 합성곱 신경망 2 CNN (0) | 2024.04.21 |
|---|---|
| 강화 학습 중간 정리 3 - MDP 모를 때 최적 정책 찾기 (0) | 2024.04.21 |
| 강화 학습 중간 정리 1 - MC, 마르코프 프로세스, MDP, MRP, 벨만 방정식 (1) | 2024.04.20 |
| 강화 학습 정리 - 6장 MDP를 모를 때 최고의 정책 찾기 (0) | 2024.04.20 |
| 강화 학습 정리 5강 - MDP를 모를 때 밸류 평가하기 (34) | 2024.04.20 |