MDP를 모른다 - 모든 상태에서 보상을 모른다. 가보기 전(경험)에 모른다. 정의되어 있을 순 있다. -> 우리가 살아가는 방식
MC- full batch, 통계에서도 사용한다. 그냥 해봐서 데이터 쌓기.

리턴 최대화 == 리워드 누적 합 최대화
경험해봐야 안다 == MC는 끝날 때 까지 그냥 한다.
특정 state를 가기 전에는 보상을 모른다!
가서 알게 된다!
최적 정책: 리워드의 총합인 리턴의 최대화
리턴 : 끝날 때 까지의 합 이므로 끝나기 전에는 모른다. - MC
끝까지 가기 어렵다! - TD
V를 계산하는 과정 중에서 v를 재귀적으로 구하는 방법이 있었다.
끝까지 가지 않더라도 근사화 된 값을 사용할 수 있다.

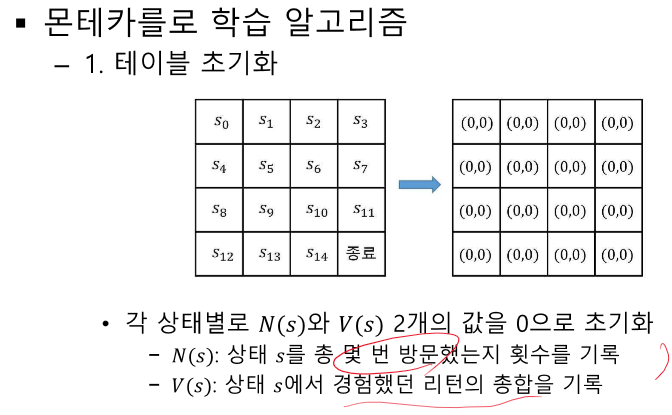
N, V 따로 안하면 매순간 평균으로 업데이트한다.
value : 리워드의 총합 - 보상 모르는데?
ㄴ 모든 상태를 경험해 본 것이 아니다. 전이 확률을 모른다.(이전엔 1로 두고 풀었다.)

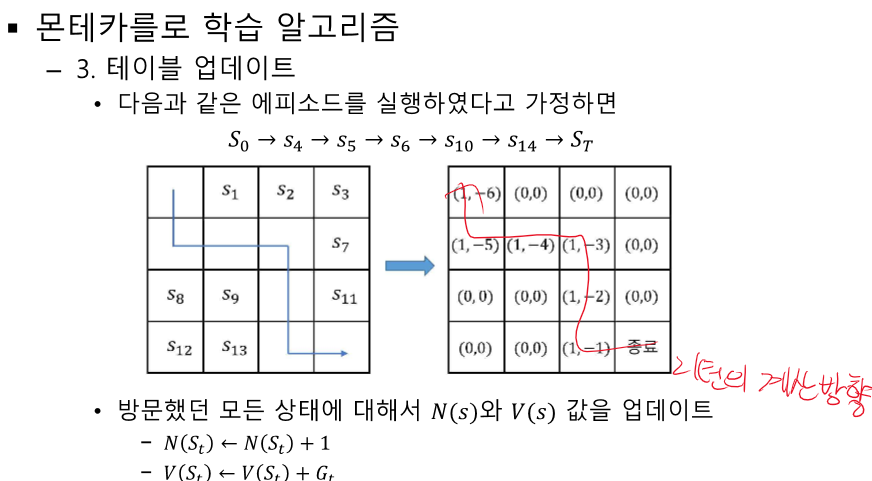
역방향으로 업데이트 된다.

정책을 고려한다 - 정책이 정해지면 따른다.
적어도 모든 S를 몇번 이상은 지나게 정책 필요

알파 - 기존 값에 얼마나 변화를 줄 거냐. 크면 극단적인 변화
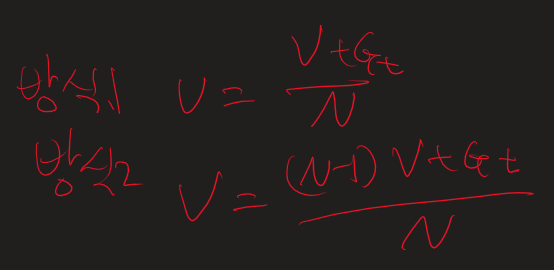




1스탭 만큼의 v를 활용한다. -> n 스탭만큼 가고 싶다 == n-step TD -> N이 에피소드 끝날때 까지 간다 == MC




MC - 편향성이 낮아지고, 분산이 커진다.
TD- 반대 (아직 끝까지 가보지 않았고, 바로 다음 값을 사용하기 때문에 잘못된 길을 갈 수 있다.)

분산이 작다 == 상대적으로 변화량이 작다.

리턴의 정의 : 에피소드 끝날 때 까지 리워드의 총합
N-step TD : 다음 스텝의 리워드를 사용할 수 있다. - N step return


람다 - 평균을 만드는 역할을 한다.

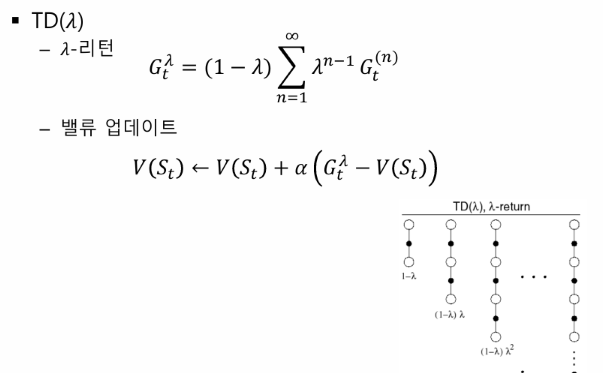
대부분의 경우 무한대가 아니다!
적정한 n값을 설정해줘야 한다.
람다가 0 이면? 정의가 이상해진다.
1도 앞이 0이라서 이상해진다.
-> 람다가 0, 1일 때 스위칭을 한다. MC와 TD
'인공지능 > 공부' 카테고리의 다른 글
| 강화 학습 중간 정리 1 - MC, 마르코프 프로세스, MDP, MRP, 벨만 방정식 (1) | 2024.04.20 |
|---|---|
| 강화 학습 정리 - 6장 MDP를 모를 때 최고의 정책 찾기 (0) | 2024.04.20 |
| 강화 학습 정리 - 4강 MDP를 알 때의 플래닝 (1) | 2024.04.20 |
| 강화 학습 정리 - 3강 벨만 방정식 (1) | 2024.04.20 |
| 강화학습 정리 - 1강 강화학습이란? (0) | 2024.04.20 |