
정책 이터레이션이 뭐였지?

정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때 까지 반복하는 방법론
P를 모른다 == 내가 어떤 S로 갈 지 모른다.
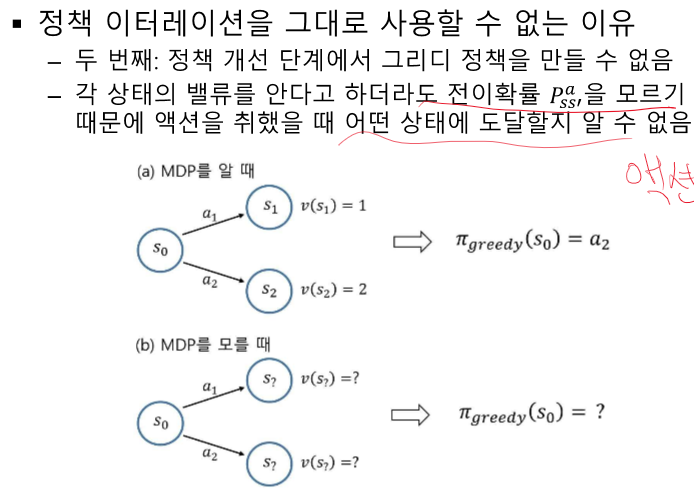
액션과 value의 매칭이 안된다.

여기서 한번 간 길을 계속 가게 될 수 있어 최적 값이 아니거나 길을 못 찾을 수도 있어 랜덤값을 추가한다.

랜덤 값으로 인해 최적길을 찾아주고, P를 모르기 때문에 다양한 경험을 한다.
학습이 진행될 수록 점점 정확해지기 때문에 그 땐 없앤다.
Max가 되는 a를 선택하는게 일반적인 정책
BUT 최적의 정책인지 확실하지 않다.
리워드가 생기기 시작하면 더 따라가기 때문에 정책 정의 할 때 랜덤 값 추가 == 입실론 그리디!


Q를 계속해서 업데이트 -> max Q 값은?
Q 테이블 - 모든 s와 a에 대해 다 들어있음
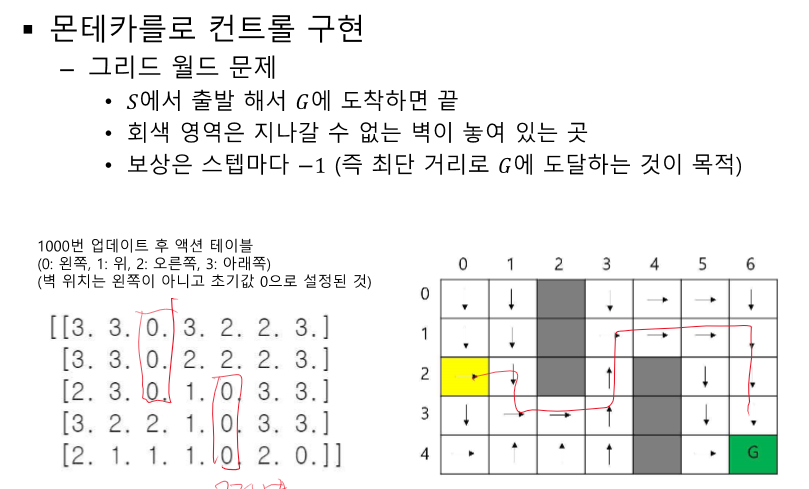
MDP가 모를 때 정책을 찾기 위해 Q를 사용하기 시작
Q를 사용하는 방법 MC와 TD
TD - 살사

MDP를 모른다
S에서 특정 A를 취했을 때 리워드이다.
여기가 더 커야한다. BUT 상수 하나로 되어있다. (4방향 다 -1이다)
그러나 한 개로 둔다.
그리드 월드이기 때문이다.
Rs = E(Rsa) - 다 동일하게 -1이기 때문에 성립한다.
모든 액션에 대한 평균값!
V(s) = E(Q(s,a))와 마찬가지



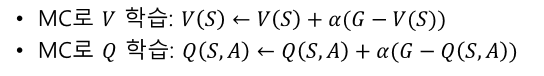
V에선 s에 대한 리워드
Q에선 s에서 a를 취했을 때 리워드



타겟 - 기존의 정책을 사용하겠다.
행동 - (정책을 따라)이동하면서 v와 q를 업데이트하며 정책을 찾겠다.

이 전의 방식 - 정책에 의존하여 경험

벨만 기대 방정식 - 정책에 따라 움직이면서 계산
이전 방식 - 평균을 사용
현재 - MAX
G - 정책이 정의가 되어있다 -> a가 정해져 있다.
벨만 최적을 쓴다 - 가장 좋은 Q값을 사용한다.
이전과의 차이점 - 그냥 찾는 것이 아니라 정책을 따라 이동하면서 찾는다.
허용된 경우의 수가 적을 수 있다.
TD - 완벽하지 않은 상황에서 max를 찾는게 맞냐!
Q러닝 - 그래서 전체 중에 max를 찾는다.




식의 모양이 조금 다르다
살사 - 파이 정책을 따르면서 맥스(혹은 입실론 만큼의 랜덤)가 되는 q를 가져와 찾는다.
Q러닝 - q 업데이트 하는 과정에서 파이를 무시하고 전체중에 맥스를 찾자!

safe path - 마이너스가 크게 쌓인다 - Sarsa
optimal path - 최단 길을 찾으나 빠질 확률이 크다 - Q
살사는 안정적인 길을 선호한다.
Q는 맥스를 가기 때문의 최적 길을 선호한다.



'인공지능 > 공부' 카테고리의 다른 글
| 강화 학습 중간 정리 2 - MDP planning, MDP X value평가, X planning (0) | 2024.04.20 |
|---|---|
| 강화 학습 중간 정리 1 - MC, 마르코프 프로세스, MDP, MRP, 벨만 방정식 (1) | 2024.04.20 |
| 강화 학습 정리 5강 - MDP를 모를 때 밸류 평가하기 (34) | 2024.04.20 |
| 강화 학습 정리 - 4강 MDP를 알 때의 플래닝 (1) | 2024.04.20 |
| 강화 학습 정리 - 3강 벨만 방정식 (1) | 2024.04.20 |