Self-Consistency Improves Chain of Thought Reasoning in Language Models

https://arxiv.org/abs/2203.11171

Self-Consistency Improves Chain of Thought Reasoning in Language Models

 

기존 LLM을 활용한 CoT에선 Greedy Decoding 방식을 따른다.

CoT방식이 모델의 성능을 올려주는 것은 확실했으나 단 하나의 Reasoning path를 따르기에 Local Optimality 문제를 야기했다.

그리하여 Self-Consistencty 방식을 제안한다.

SC

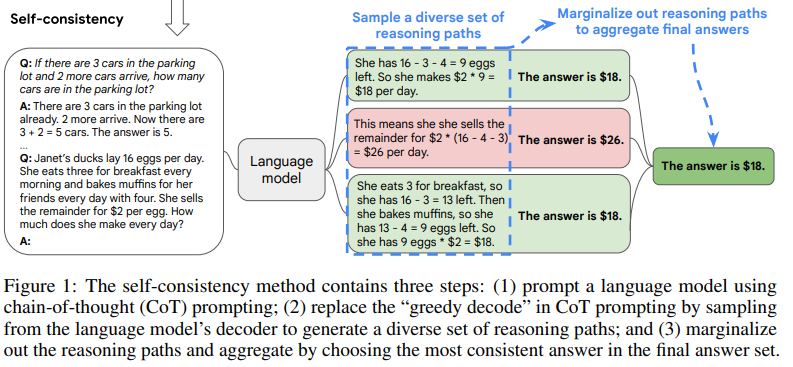
Temperature, Top-k 등 다양한 방식을 통해 여러 Reaoning 을 도출하고, 여기서 가장 많은 수의 답을 뽑거나, 우도(Likelihood)을 통해 가중 평균하여 높은 값을 구합니다.

단순한 방법이고 생각인데 높은 성능 향상을 가져 옵니다.

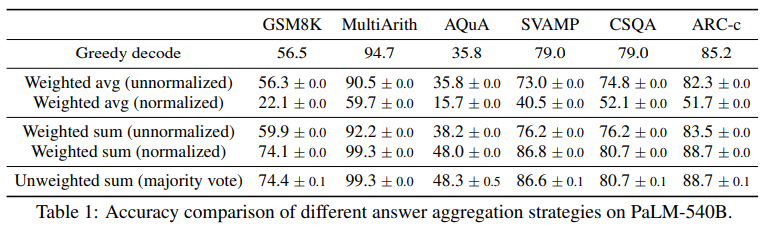
그리하여 이러한 결과를 가져왔습니다.

 

샘플 수가 증가할 수록 성능이 증가하는 것을 볼 수 있다.

SC-CoT 방식이 Beam Search보다 높은 성능을 가지는 것을 볼 수 있다.

논문에서는 다양성 부족으로 SC-CoT의 성능을 따라가지 못하는 것으로 본다.

앙상블 접근보다도 높은 성능!

 

좋은 방식인 것 같은데 천천히 파악해봐야 겠습니다 ㅎㅎ..

 

 

 

📖 연구 배경	- 기존 Chain-of-Thought(CoT) 방식이 복잡한 논리 추론 문제에서 성능을 향상시키지만, 탐욕적 디코딩(Greedy Decoding) 방식의 한계 존재. - 단일 추론 경로만을 따르기 때문에 국소 최적화(Local Optimality) 문제, 잘못된 경로 수정 불가, 추론 다양성 부족 문제 발생.
🎯 연구 목표	- Self-Consistency 기법 제안 → 다양한 추론 경로를 샘플링하고, 가장 일관된 답변을 선택하여 CoT 성능을 극대화
🛠️ Self-Consistency 방법	1️⃣ 다양한 추론 경로 생성: Temperature Sampling, Top-k Sampling 등 활용하여 서로 다른 reasoning paths 생성. 2️⃣ 정답 선택 방식 개선: Majority Voting(다수결) 또는 Weighted Sum(확률 가중 평균) 방식 적용. 3️⃣ 오류 보정: 다수의 reasoning path를 비교하여 오류 가능성이 높은 경로 자동 제거.
📊 실험 설정	- Benchmark Tasks: 산술 추론(GSM8K, SVAMP, AQuA 등), 상식 추론(CommonsenseQA, ARC 등), 기호적 추론(Coinflip 등) - 사용 모델: UL2-20B, GPT-3(175B), LaMDA-137B, PaLM-540B - 샘플링 기법: Temperature Sampling (T=0.5~0.7), Top-k (k=40)
🚀 실험 결과	- 모든 모델과 태스크에서 CoT보다 성능 향상 - 산술 추론 (GSM8K): CoT(56.5%) → Self-Consistency(74.4%, +17.9%) - 상식 추론 (ARC-Challenge): CoT(85.2%) → Self-Consistency(88.7%, +3.5%) - 특히, 모델 크기가 커질수록 효과 증가 (PaLM-540B에서 가장 큰 성능 향상)
🔄 Self-Consistency vs 기존 방법	1️⃣ vs. Beam Search - Beam Search는 탐색 경로가 제한적이라 다양성이 부족하여 국소 최적화 발생 - Self-Consistency는 다양한 reasoning path를 활용하여 더 나은 정답 도출 가능 - 실험 결과: Self-Consistency(14.7%) > Beam Search(10.7%) (MultiArith Task) 2️⃣ vs. Ensemble Methods - 여러 개의 모델을 조합하는 기존 앙상블보다 Self-Consistency가 성능이 뛰어남 - Prompt Order Permutation (60.9%) vs. Self-Consistency (74.4%) (GSM8K Task) - 하나의 모델만으로도 자체적인 앙상블 효과(Self-Ensemble) 가능
💡 추가 실험 결과	- Self-Consistency는 샘플링 방법(Temperature, Top-k 등)에 관계없이 안정적인 성능 향상 - Zero-Shot CoT에서도 효과적 → 성능 +26.2% 향상 - 잘못된 프롬프트 사용 시에도 성능 감소 방지 (17.1% → 23.4%)
📌 결론 및 의의	✅ Self-Consistency는 CoT의 성능을 혁신적으로 향상 🚀 ✅ 추론 다양성을 극대화하여 더 강력한 reasoning 능력을 제공 ✅ 기존 Beam Search 및 앙상블 기법보다 효과적이며, 추가 학습 없이 적용 가능

 

1. 연구 배경 및 문제 정의

기존의 대형 언어 모델(Large Language Models, LLMs)은 다양한 자연어 처리(NLP) 작업에서 뛰어난 성능을 보였지만, 논리적 추론(reasoning) 능력에서 한계를 보였다. 이를 개선하기 위해 Chain-of-Thought (CoT) Prompting이 제안되었으며, 이는 사람이 문제를 해결하는 과정과 유사한 방식으로 모델이 논리적 단계를 생성하도록 유도하는 기법이다.

그러나 기존의 CoT 방법은 탐욕적 디코딩(Greedy Decoding) 방식을 사용하여 단 하나의 추론 경로(reasoning path)만을 따르기 때문에 국소 최적화(local optimality) 문제를 야기한다. 이를 해결하기 위해 본 연구에서는 Self-Consistency (SC) 라는 새로운 디코딩 전략을 제안했다.

---

2. 연구 목표

Self-Consistency 기법을 통해:

1. 모델이 문제를 해결하는 다양한 추론 경로를 생성하도록 유도하고,
2. 이 경로들을 비교하여 가장 일관된 답변(the most consistent answer) 을 선택함으로써,
3. 기존 CoT보다 더 정확하고 안정적인 추론 성능을 달성하는 것이 목표이다.

---

3. Self-Consistency 기법의 핵심 아이디어

Self-Consistency는 다음과 같은 과정으로 이루어진다:

1. 다양한 추론 경로 생성
   • 기존의 Greedy Decoding 방식이 하나의 최적화된 경로만 탐색하는 것과 달리, 다양한 샘플링 기법(temperature sampling, top-k sampling, nucleus sampling 등)을 활용하여 다수의 가능한 추론 경로를 생성한다.
2. 다양한 경로에서 도출된 정답 비교 및 집계
   • 모델이 생성한 여러 개의 추론 경로마다 서로 다른 최종 정답이 나올 수 있다.
   • 다수결(Majority Voting) 방식을 사용하여 가장 많이 등장하는 정답을 선택함으로써, 모델이 가장 신뢰할 수 있는 결과를 도출하도록 유도한다.
3. 국소 최적화 및 불확실성 감소
   • Greedy Decoding은 동일한 데이터를 반복적으로 생성할 가능성이 높지만, Self-Consistency는 더 다양한 해결 방식을 고려할 수 있도록 함으로써 국소 최적화 문제를 해결한다.
   • 또한, 잘못된 추론 경로가 포함되더라도 다수결 집계를 통해 오류를 줄일 수 있는 강건성(robustness)을 제공한다.

---

4. 실험 설정 및 평가 방법

Self-Consistency 기법의 효과를 검증하기 위해 다양한 데이터셋과 모델을 대상으로 실험을 수행했다.

4.1 실험 대상 데이터셋

다음과 같은 산술 추론(Arithmetic Reasoning) 및 상식 추론(Common Sense Reasoning) 문제를 포함하는 데이터셋을 사용했다:

• GSM8K (초등학교 수준의 수학 문제)
• SVAMP, AQuA, StrategyQA (추론 능력을 평가하는 벤치마크)
• ARC-Challenge, CommonsenseQA (일반적인 상식 및 논리적 사고 능력을 평가하는 문제)

4.2 실험에 사용된 언어 모델

Self-Consistency의 효과를 다양한 모델 크기에서 검증하기 위해 4개의 대형 언어 모델을 활용했다:

• UL2-20B
• GPT-3 175B
• LaMDA-137B
• PaLM-540B

모든 실험은 few-shot learning 방식으로 진행되었으며, 모델을 추가로 학습시키지 않고 기존 사전 학습된 모델을 활용했다.

---

5. 실험 결과 및 분석

Self-Consistency 기법을 적용한 결과, 기존 Chain-of-Thought 방식보다 크게 향상된 성능을 보였다.

5.1 산술 추론(Arithmetic Reasoning) 성능 향상

모델	GSM8K	SVAMP	AQuA
CoT-Prompting	56.5%	79.0%	35.8%
Self-Consistency	74.4% (+17.9%)	86.6% (+7.6%)	48.3% (+12.5%)

• GSM8K에서는 17.9%의 절대 정확도 향상을 보였으며, 다른 수학 문제 데이터셋에서도 7~12% 이상의 성능 향상을 기록했다.

5.2 상식 추론(Common Sense Reasoning) 성능 향상

모델	StrategyQA	ARC-Challenge
CoT-Prompting	75.3%	85.2%
Self-Consistency	81.6% (+6.3%)	88.7% (+3.5%)

• 상식 추론에서도 모든 모델에서 개선된 성능을 기록했으며, 특히 더 복잡한 reasoning task에서 효과적이었다.

5.3 Self-Consistency 기법의 강점

1. 다양한 모델 크기에서 효과적
   • UL2-20B 같은 중간 크기의 모델에서도 성능 향상을 확인.
   • PaLM-540B, GPT-3 같은 초대형 모델에서는 최신 SOTA(State-of-the-Art) 성능 달성.
2. 기존의 CoT 방식보다 더 높은 정답 일관성(Consistency) 보장
   • 여러 개의 reasoning path를 고려하는 방식이므로, 잘못된 reasoning을 제거하고 신뢰할 수 있는 답변을 도출하는 데 강점이 있음.
3. 기존 방법들과의 비교
   • 기존의 Sample-and-Rank, Beam Search, Ensemble 방법들보다 더 나은 성능을 보여줌.
   • 특히 Beam Search보다 다양한 reasoning path를 활용할 수 있어 성능이 더 좋음.

---

6. 연구의 한계 및 향후 과제

6.1 계산 비용 증가

• Self-Consistency는 다수의 샘플을 생성해야 하므로 연산 비용이 증가하는 단점이 있다.
• 하지만 실험 결과, 5~10개 정도의 샘플링만으로도 상당한 성능 향상을 달성할 수 있었음.

6.2 다양한 NLP 작업으로의 확장

• 본 연구는 주로 산술 및 상식 추론에 초점을 맞추었으나, 더 복잡한 reasoning task(ex. 과학적 논증, 법률 논리 등)에 Self-Consistency를 적용할 가능성이 있다.

6.3 모델의 불확실성 추정

• Self-Consistency 기법은 모델이 얼마나 일관된 답변을 생성하는지를 평가하는 메트릭으로 활용 가능함.
• 즉, 모델이 스스로 "모르겠다"고 판단할 경우, 추가적인 검토가 필요하다는 신호로 활용할 수 있음.

---

7. 결론

Self-Consistency는 Chain-of-Thought 추론을 강화하는 강력한 디코딩 전략으로, 기존 방식보다 뛰어난 성능을 보인다.
특히, 여러 개의 추론 경로를 생성하고 이를 집계하는 방식이 NLP 모델의 reasoning 능력을 극대화할 수 있음을 실험적으로 입증했다.

향후 연구에서는 계산 효율성을 개선하고, 다양한 reasoning task에 적용 가능성을 확장하는 방향으로 발전이 가능할 것으로 보인다. 🚀

 

Self-Consistency 방식

Self-Consistency는 기존의 탐욕적 디코딩(Greedy Decoding) 을 대체하는 새로운 디코딩 기법으로, 다양한 추론 경로를 탐색하여 가장 일관된 답변을 선택하는 방식이다. 이 접근법은 "서로 다른 방식으로 문제를 풀었을 때 같은 정답이 나오면 신뢰도가 높아진다"는 인간의 직관을 반영한다.

---

1. 기존 Chain-of-Thought(Greedy Decoding)의 한계

기존의 Chain-of-Thought(CoT) 방식은 다음과 같은 절차로 동작한다:

1. 모델이 문제를 받으면 하나의 최적화된 추론 경로(reasoning path)를 따라가며 답변을 생성한다.
2. 이 과정에서 단 하나의 해결 방법만 사용하기 때문에, 잘못된 경로를 따라가면 오류를 수정할 기회가 없다.
3. 국소 최적화(local optimality) 문제로 인해 정답이 아님에도 모델이 스스로 신뢰하는 답변을 출력할 수 있다.

---

2. Self-Consistency의 핵심 원리

Self-Consistency는 하나의 추론 경로에 의존하는 대신, 여러 개의 추론 경로를 생성하고 그중 가장 일관된 답을 선택하는 방식으로 동작한다.
주요 과정은 다음과 같다:

1. 다양한 추론 경로 생성 (Diverse Reasoning Paths Sampling)
   • 기존의 CoT 방식처럼 모델을 통해 문제 해결 과정을 생성하지만, 탐욕적 디코딩을 사용하지 않고 다수의 샘플링을 수행한다.
   • 이를 위해 Temperature Sampling, Top-k Sampling, Nucleus Sampling 등의 다양한 샘플링 기법을 활용한다.
   • 이 과정에서 서로 다른 사고 방식을 반영한 여러 개의 가능한 해결 경로(reasoning paths) 가 생성된다.
2. 다양한 정답 도출 및 집계 (Answer Aggregation)
   • 생성된 각 추론 경로는 서로 다른 최종 정답을 포함할 가능성이 있음.
   • Self-Consistency는 모든 정답을 수집하고, 다수결(Majority Voting) 을 수행하여 가장 자주 등장하는 정답을 최종 선택한다.
   • 이를 통해 잘못된 추론 경로에서 도출된 오류를 자동으로 걸러낼 수 있음.
3. 확률 기반 정답 선택 (Weighted Aggregation)
   • 단순 다수결 외에도, 각 경로의 확률 값을 활용하여 가중 평균(Weighted Average) 방식으로 정답을 선택할 수도 있다.
   • 특정 경로가 상대적으로 더 신뢰할 만한 정보(높은 확률 값)를 포함하는 경우, 이를 더 반영하여 정답을 결정하는 방식이다.

---

3. Self-Consistency의 장점

✅ Greedy Decoding의 국소 최적화 문제 해결
✅ 잘못된 추론 경로를 걸러내어 정답 신뢰도 향상
✅ 다양한 샘플링 방식을 통해 더 풍부한 사고 과정 반영 가능
✅ 기존 모델을 변경하지 않고 바로 적용 가능 (Fine-tuning 불필요)
✅ 특히 수학 문제 풀이, 논리적 추론 문제에서 성능이 크게 향상됨

---

📌 예제를 통한 이해

아래는 Self-Consistency 방식이 어떻게 동작하는지를 보여주는 예제이다.

문제

Janet의 오리들은 하루에 16개의 알을 낳는다.
그녀는 매일 아침 3개를 먹고, 친구들을 위해 머핀을 만들 때 4개를 사용한다.
남은 알을 개당 $2에 판매한다면, 하루에 얼마를 벌 수 있을까?

---

🔴 기존 Greedy Decoding 방식 (단일 추론 경로)

1. 모델의 추론 과정
   • "Janet의 오리는 하루에 16개의 알을 낳는다."
   • "그녀는 아침마다 3개를 먹는다. 16 - 3 = 13"
   • "그녀는 머핀을 만들 때 4개를 사용한다. 13 - 4 = 9"
   • "그녀는 9개의 알을 판매한다. 가격은 $2이므로, 9 × 2 = $18"
   • 최종 답변: "$18"

✅ 정답에 도달했지만, 하나의 경로만 고려했기 때문에 신뢰도가 낮음.

---

🟢 Self-Consistency 방식 (다양한 추론 경로 활용)

Self-Consistency에서는 여러 개의 해결 방식을 샘플링하여 다양한 추론 경로를 고려한다.

1️⃣ 추론 경로 1

• "Janet의 오리는 하루에 16개의 알을 낳는다."
• "그녀는 아침마다 3개를 먹는다. 16 - 3 = 13"
• "그녀는 머핀을 만들 때 4개를 사용한다. 13 - 4 = 9"
• "그녀는 9개의 알을 판매한다. 가격은 $2이므로, 9 × 2 = $18"
• 답변: "$18"

2️⃣ 추론 경로 2

• "그녀는 매일 3개의 알을 먹고, 4개를 사용한다. 즉, 하루에 3 + 4 = 7개를 소비한다."
• "따라서 남는 알의 개수는 16 - 7 = 9개이다."
• "각 알을 $2에 판매하므로, 총 수익은 9 × 2 = $18"
• 답변: "$18"

3️⃣ 추론 경로 3 (오류 포함)

• "그녀는 총 16개의 알을 낳고, 4개를 사용한다. 즉, 남은 개수는 16 - 4 = 12"
• "그녀는 12개의 알을 $2에 판매한다. 따라서 12 × 2 = $24"
• 오답: "$24"

---

🟢 Self-Consistency 결과: 다수결 집계

• $18 (2번 등장)
• $24 (1번 등장, 오류 포함)
• 가장 많이 등장한 $18이 최종 정답으로 선택됨 ✅

💡 결과적으로, 잘못된 경로(오답 $24)를 자동으로 걸러내고 가장 신뢰할 수 있는 정답을 선택할 수 있음.

---

📌 요약

Self-Consistency는 기존 Greedy Decoding과 어떻게 다른가?

방식	기존 CoT	SC-CoT
추론 경로	하나의 고정된 경로	다양한 경로 샘플링
정답 선택 방식	단일 정답 선택	다수결 방식으로 신뢰도 높은 답 선택
오류 보정	잘못된 경로를 수정할 기회 없음	틀린 경로 자동 필터링
일관성(Consistency)	낮음	높음
계산 비용	낮음 (1회 추론)	상대적으로 높음 (다중 샘플링)

결론: Self-Consistency는 다수의 추론 경로를 탐색하여 가장 신뢰할 수 있는 답변을 선택하는 강력한 기법이다.
특히 수학 문제 풀이, 논리적 추론 문제에서 성능 향상이 두드러지며, 다양한 NLP 태스크에도 적용 가능성이 크다. 🚀

 

Self-Consistency에서 가중 평균(Weighted Average) 계산 방법

Self-Consistency 방식에서는 단순 다수결(Majority Voting)뿐만 아니라, 각 정답에 가중치(weight) 를 부여하여 최적의 답변을 선택하는 방법도 사용할 수 있다. 이 과정에서 사용되는 확률 값은 언어 모델이 특정 단어를 생성할 확률(우도, likelihood) 을 기반으로 한다.

---

📌 1. 확률 값은 어디서 오는가?

언어 모델은 각 단어(또는 토큰)를 생성할 때 확률 값을 할당한다.
이 확률 값은 "모델이 해당 단어를 다음 토큰으로 선택할 가능성" 을 나타낸다.

💡 즉, 우도(likelihood) 값이라고 볼 수 있으며, 수식으로 표현하면 다음과 같다.

---

📌 2. 가중 평균(Weighted Sum) 계산 방법

Self-Consistency에서 각 정답 후보 a_i 에 대해 확률 P(a_i | Q, P) 를 계산한 뒤, 이를 가중치로 사용하여 최종 답을 결정할 수 있다.

✔ 가중 평균 공식

이 방식은 확률이 높은 정답일수록 더 큰 영향을 주도록 조정하는 역할을 한다.

---

📌 3. 예제: 수학 문제에 Self-Consistency 적용

문제

Janet의 오리들은 하루에 16개의 알을 낳는다.
그녀는 매일 3개를 먹고, 4개를 사용한다.
남은 알을 개당 $2에 판매한다면, 하루에 얼마를 벌 수 있을까?

🔴 Step 1: 모델이 여러 개의 답변을 생성

정답 후보 (a_i)	계산 과정	확률 값 (P(a_i | Q, P))
$18	(16 - 3 - 4) * 2 = $18	0.60
$18	3 + 4 = 7, 16 - 7 = 9, 9 * 2 = $18	0.30
$26 (오답)	(16 - 4 - 3) * 2 = $26 (잘못된 연산)	0.10

 

---

🟢 Step 2: 가중 평균 계산

✅ 최종 정답: "$18" (오답 "$26"이 가중치가 낮아 영향력이 줄어듦)

---

📌 4. 가중 평균 vs 다수결 (Majority Voting)

방법	특징	장점	단점
다수결 (Majority Voting)	가장 많이 등장한 정답을 선택	계산이 단순하고 직관적	낮은 확률의 정답도 같은 가중치
가중 평균 (Weighted Sum)	확률 값을 반영하여 정답 선택	더 신뢰할 수 있는 답변 선택 가능	확률 값이 필요함

• 다수결 방식은 오답이 더 많이 등장하면 오류 가능성이 있음.
• 가중 평균 방식은 정확도가 높은 답변을 더 반영할 수 있음.

---

📌 5. 결론

✅ Self-Consistency에서 가중 평균(Weighted Sum)은 각 정답의 확률 값을 반영하여 신뢰도 높은 답변을 선택하는 방법
✅ 확률 값은 모델이 단어를 선택할 때 내부적으로 계산하는 "우도 값(likelihood)"을 기반으로 함
✅ 수학 문제, 논리 추론 문제 등 정답이 고정된 태스크에서 강력한 성능을 발휘함

즉, Self-Consistency에서 확률 값을 활용한 가중 평균 계산은 단순 다수결보다 더 정교한 답변 선택이 가능하도록 한다! 🚀

 

 

논문에서는 Self-Consistency 방식의 효과를 검증하기 위해 다양한 데이터셋과 기존 기법들과 비교 실험을 수행했다. 실험은 다양한 언어 모델과 샘플링 방법을 사용하여 reasoning(추론) 성능을 평가하는 방식으로 진행되었다.

---

📌 1. 실험 설정 (Experiment Setup)

(1) 사용된 태스크 및 데이터셋

Self-Consistency 방식의 성능을 평가하기 위해 다양한 추론(Reasoning) 문제에 대한 벤치마크 데이터셋을 활용하였다. 크게 산술 추론(Arithmetic Reasoning), 상식 추론(Common Sense Reasoning), 기호적 추론(Symbolic Reasoning) 으로 구분된다.

추론 유형	사용된 데이터 셋	설명
산술 추론 (Arithmetic Reasoning)	AddSub, MultiArith, ASDiv, AQuA-RAT, GSM8K, SVAMP	수학 문제 해결 (예: 수열, 방정식 등)
상식 추론 (Commonsense Reasoning)	CommonsenseQA, StrategyQA, ARC	일반적인 상식과 논리를 활용한 문제 해결
기호적 추론 (Symbolic Reasoning)	Last Letter Concatenation, Coinflip	문자열 조작, 논리적 사고 문제

---

(2) 사용된 언어 모델 (Language Models)

Self-Consistency가 모델 크기와 관계없이 효과적인지 검증하기 위해 4개의 서로 다른 크기의 대형 언어 모델을 사용하였다.

모델	파라미터 수	특징
UL2-20B	20B	Encoder-Decoder 모델, 오픈소스
GPT-3 (Codex)	175B	OpenAI의 GPT-3 시리즈
LaMDA-137B	137B	Google Research의 대화형 모델
PaLM-540B	540B	Google의 대형 Transformer 모델

✔ 모든 실험은 Few-shot Learning 환경에서 진행
✔ 모델을 추가로 학습(Fine-tuning)하지 않고, 이미 학습된 모델을 그대로 사용하여 평가
✔ 공정한 비교를 위해 동일한 Chain-of-Thought (CoT) 프롬프트를 사용 (Wei et al., 2022 방식 활용)

---

(3) 샘플링 기법 (Sampling Scheme)

Self-Consistency에서는 다양한 추론 경로를 생성해야 하므로 다양한 샘플링 기법을 사용하였다.

모델	샘플링 방법	설정 값
UL2-20B, LaMDA-137B	Temperature Sampling + Top-k Sampling	T = 0.5, k = 40
PaLM-540B	Temperature Sampling + Top-k Sampling	T = 0.7, k = 40
GPT-3 (Codex)	Temperature Sampling	T = 0.7 (Top-k 미적용)

✔ Temperature Sampling: 모델이 다음 단어를 생성할 때 확률 분포를 조정하는 방법
✔ Top-k Sampling: 확률이 높은 상위 k개의 단어만 후보로 선택

---

📌 2. 주요 실험 결과 (Main Results)

논문에서는 Self-Consistency의 성능을 기존의 Chain-of-Thought + Greedy Decoding(CoT-Prompting) 과 비교하여 분석했다.

(1) 산술 추론 성능 향상

모델	GSM8K	SVAMP	AQuA
CoT-Prompting	56.5%	79.0%	35.8%
Self-Consistency	74.4% (+17.9%)	86.6% (+7.6%)	48.3% (+12.5%)

✅ Self-Consistency는 모든 모델에서 성능을 향상시켰으며, 특히 큰 모델일수록 더 큰 성능 향상
✅ GSM8K 같은 복잡한 문제에서는 17.9%의 절대 정확도 향상

---

(2) 상식 추론 및 기호적 추론 성능 향상

	StrategyQA	ARC-Challenge
CoT-Prompting	75.3%	85.2%
Self-Consistency	81.6% (+6.3%)	88.7% (+3.5%)

✅ 상식 및 논리 추론에서도 성능 개선을 확인
✅ 특히, Out-of-Distribution(OOD) 테스트에서도 강력한 성능을 보임

---

(3) Self-Consistency가 Chain-of-Thought보다 유리한 경우

논문에서는 기존 연구(Ye & Durrett, 2022)에서 발견된 문제점인 "Chain-of-Thought 방식이 오히려 성능을 낮추는 경우" 를 분석하였다.

1. 일부 NLP 태스크에서는 CoT 방식이 Standard Prompting보다 오히려 성능이 낮아지는 문제가 존재.
2. 하지만 Self-Consistency를 적용하면 이 문제를 해결하고, Standard Prompting보다 높은 성능을 달성함.

Task	Standard Prompting	CoT	SC-CoT
ANLI R1	69.1%	68.8%	78.5% (+9.4%)
e-SNLI	85.8%	81.0%	88.4% (+7.4%)
RTE	84.8%	79.1%	86.3% (+7.2%)

✔ Self-Consistency는 CoT의 단점까지 보완할 수 있음! 🚀

---

📌 3. 기존 방법들과의 비교 (Comparison to Other Methods)

Self-Consistency가 기존의 디코딩 방법보다 우수한지 확인하기 위해 다양한 방식과 비교 실험을 수행했다.

(1) Sample-and-Rank 방식과 비교

• Sample-and-Rank 방식은 여러 개의 응답을 생성한 뒤 확률 값을 기반으로 최상위 응답을 선택하는 방식이다.
• 그러나 Self-Consistency보다 성능 향상이 적음이 확인됨.

(2) Beam Search 방식과 비교

• Beam Search는 한 번에 여러 개의 탐색 경로를 따라가며 최적의 답을 찾는 방식.
• 하지만 다양성이 부족하여(Self-Consistency 대비) 성능이 낮음이 확인됨.

모델	AQuA	MultiArith
Beam Search	23.6%	10.7%
Self-Consistency (Sampling 기반)	26.9% (+3.3%)	14.7% (+4.0%)

(3) Ensemble 방식과 비교

• 여러 개의 모델을 함께 활용하는 Ensemble 기법과 비교했을 때도, Self-Consistency가 더 높은 성능을 보임.

	GSM8K
모델 앙상블 (3개 모델 결합)	36.9%
Self-Consistency (PaLM-540B 단일 모델)	74.4% (+37.5%)

✔ Self-Consistency는 하나의 모델만 사용하면서도 앙상블보다 높은 성능을 달성!

---

📌 4. 추가 실험 (Additional Studies)

1. Self-Consistency가 다양한 샘플링 방법에도 강건한지(robust) 확인 → 모든 샘플링 기법에서 성능 향상 확인됨.
2. 잘못된 프롬프트가 주어졌을 때 성능 감소 여부 분석 → Self-Consistency가 오히려 이를 보완하는 효과가 있음.

---

📌 5. 결론

✅ Self-Consistency는 기존 CoT-Prompting보다 모든 추론 태스크에서 뛰어난 성능을 보임
✅ 샘플링 기법을 활용해 다양한 사고 방식을 반영할 수 있어 기존 디코딩 기법보다 강력
✅ 특히 큰 모델일수록 효과가 더 뚜렷하며, NLP 일반 문제에도 효과적으로 적용 가능

🚀 결론적으로, Self-Consistency는 reasoning 성능을 혁신적으로 향상시키는 강력한 기법이다! 🚀

 

Self-Consistency vs. Beam Search & 앙상블 기법 비교 분석

논문에서는 Self-Consistency의 성능을 기존의 대표적인 디코딩 방식인 Beam Search 및 앙상블(Ensemble) 기법과 비교하여 분석하였다.
이 과정에서 Self-Consistency가 기존 방법들보다 더 뛰어난 성능을 보인 이유를 살펴본다.

---

📌 1. Beam Search와의 비교

Beam Search는 NLP 모델의 대표적인 디코딩 기법으로,
단순한 Greedy Decoding보다 더 나은 최적해를 찾기 위해 사용된다.

🔹 Beam Search란?

• Beam Search는 여러 개의 후보 문장을 동시에 탐색하며, 확률이 가장 높은 문장들을 유지하는 방식.
• k 개의 후보(beam)를 유지하며 확률값이 높은 상위 k 개의 결과만 남기면서 탐색을 확장함.
• 최종적으로 가장 높은 확률을 가진 문장을 선택.

✅ 장점
✔ Greedy Decoding보다 더 나은 결과 도출 가능
✔ 최적의 문장을 찾기 위해 확률 기반 탐색 진행

❌ 단점
✖ 다양성이 부족 → 모든 Beam이 비슷한 경로를 따르게 됨
✖ 모델이 초기 선택한 방향에서 크게 벗어나지 못함
✖ Self-Consistency처럼 다양한 사고 방식을 반영하기 어려움

---

🔹 논문에서의 실험 결과

논문에서는 UL2-20B 모델에서 Self-Consistency와 Beam Search를 동일한 조건에서 비교하였다.

방법	AQuA (산술 추론)	MultiArith (산술 추론)
Beam Search (Top beam 선택)	23.6%	10.7%
Self-Consistency (Sampling 기반)	26.9% (+3.3%)	14.7% (+4.0%)

🔹 Self-Consistency가 Beam Search보다 뛰어난 이유

✅ Beam Search는 다양성이 부족

• Beam Search는 여러 후보를 탐색하지만, 결국 비슷한 경로를 반복해서 따르게 됨
• 초기 선택된 경로에서 크게 벗어나지 못하는 국소 최적화 문제 발생

✅ Self-Consistency는 다양한 reasoning path를 생성

• Sampling 기반 접근법을 사용하여 모델이 더 다양한 경로를 탐색할 수 있도록 유도
• 여러 사고 방식이 반영되므로 정답을 더 신뢰성 있게 선택 가능

🔹 추가 분석: Beam Search를 Self-Consistency에 적용한 경우

논문에서는 Self-Consistency 방식에 Beam Search를 적용하여 실험도 진행했다.
즉, Self-Consistency의 추론 경로를 생성할 때 Beam Search를 활용한 것.

방법	AQuA	MultiArith
Beam Search (단독 사용)	23.6%	10.7%
Self-Consistency + Beam Search	24.6%	12.3%
Self-Consistency + Sampling	26.9%	14.7%

✔ Self-Consistency에 Beam Search를 적용해도 성능이 개선되었지만,
✔ Sampling을 사용한 Self-Consistency가 가장 우수한 성능을 기록 🚀
✔ 즉, 다양성이 더 높은 Sampling 방식이 정답 도출에 더 효과적임이 확인됨.

---

📌 2. 앙상블(Ensemble) 기법과의 비교

앙상블 기법은 여러 개의 모델을 결합하여 성능을 향상시키는 방식이다.

🔹 실험에 사용된 앙상블 방법

논문에서는 Self-Consistency와 두 가지 대표적인 앙상블 방법을 비교했다.

1️⃣ 프롬프트 순서 변경(Prompt Order Permutation)

• 모델이 민감할 수 있는 프롬프트 순서를 랜덤하게 40번 변경하여 앙상블 수행
• (예: 문제를 다르게 구성하여 모델이 같은 결론을 내는지 평가)

2️⃣ 다양한 프롬프트 세트 활용(Multiple Sets of Prompts)

• 수동으로 3가지 다른 프롬프트를 작성하여 모델을 실행한 뒤 앙상블 수행
• (예: 서로 다른 스타일의 Chain-of-Thought 사용)

---

🔹 논문에서의 실험 결과

	GSM8K (산술 추론)
CoT-Prompting (기본)	56.5%
Prompt Order Permutation (40회)	60.9% (+4.4%)
Multiple Prompts (3개 세트)	58.9% (+2.4%)
Self-Consistency (40개 샘플)	74.4% (+17.9%)

✅ Self-Consistency가 기존 앙상블 기법보다 훨씬 높은 성능을 보임! 🚀
✅ 프롬프트를 변경하는 것만으로는 한계가 있지만, Self-Consistency는 더 효과적인 다중 사고 방식 반영 가능

---

🔹 앙상블(Ensemble)과 Self-Consistency의 차이점

	전통적 앙상블	Self-Consistency
방식	여러 개의 모델을 결합하여 평균 성능 향상	하나의 모델에서 다양한 reasoning path를 활용
필요한 리소스	여러 개의 모델 학습 필요	추가 학습 없이 샘플링 기법만 활용
추론 방식	서로 다른 모델들의 결과를 결합	하나의 모델이 다양한 답을 생성 후 최적의 답 선택
성능 향상	제한적	큰 폭의 향상 가능 (특히 대형 모델에서)

✔ Self-Consistency는 모델을 여러 개 학습시키지 않고도 앙상블처럼 동작하는 효과(self-ensemble) 제공
✔ 즉, "하나의 모델이 자체적으로 다양한 답을 생성하고 그중 최적의 답을 선택하는 과정"
✔ 일반적인 앙상블 기법보다 훨씬 효율적이고, 성능 향상 폭도 더 큼! 🚀

---

📌 3. 결론

✅ Self-Consistency는 Beam Search보다 다양한 reasoning path를 생성하여 더 높은 성능을 보임.
✅ Beam Search를 Self-Consistency에 적용해도 성능이 향상되지만, Sampling 방식이 더 우수함.
✅ 기존의 모델 앙상블보다 Self-Consistency가 훨씬 강력한 성능을 보이며, 추가적인 모델 학습이 필요 없음.
✅ 결과적으로, Self-Consistency는 하나의 모델을 사용하면서도 다양한 사고 방식을 반영하여 reasoning 성능을 극대화할 수 있는 기법! 🚀