전 시간에 발사체의 움직임에 대해 배웠다.


외부에서의 힘이 없으니 중력에 의한 수직방향 속도만 신경 써 주면 된다.

Curvilnear 조건에서는 un은 항상 0이다. 그러므로 v= vt*ut이다.
즉 tangential 방향만 남는 것이다.

아래 식은 통째로 외우는 것이 좀 더 편할 것 같다.

위 사진이 속도와 가속도의 차이이다

곡률 반경은 위와 같은 식으로 구하게 된다.

여기서는 부피, 회전을 무시하고 질점만 보면 된다.


A 지점에서의 속도와 t(시간)에 따른 속도 변화이다.
이제 v를 벡터로 전환한다.

여기선 회전 반경 구하는 식을 외우냐, 못 외우냐가 관건이네요

위에서 구한 an, at를 통해 크기와, 각도를 구해줍니다.



회전반경, 속도, 시간이 다 주어져 있으므로 그냥 가지고 있는 식에 전부 때려 박으면 끝이네요

여기선 가속도만 알려줬고, A 지점에서 속도가 0으로 시작한다고 설명해 주네요

탄젠셜 방향의 가속도를 알려줬으므로 그 값을 통해 속도, 위치에 대한 식을 구할 수 있습니다.
그리하여 t를 구하고, 그 값을 통해 가속도를 구할 수 있습니다.


각도는 반시계방향이다.



항상 인공지능만 보다 보니까 이런 식에 대해 이해도가 많이 떨어져 버렸습니다....


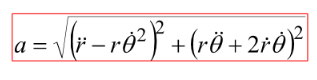

여기서 Z 축이 추가된다면!


이제 이 식만 외워봅시다...


반지름이 일정하다 보니 반지름 관련해서는 다 빠져서 결국 쉽게 구할 수 있는 문제가 되었습니다.
암기만 잘하면 될 것 같네요


여기서 velocity는 벡터값이다!

각과 반지름이 주어졌으니 각각 t로 미분하여 식을 구할 수 있다.
각도는 나온 모든 각도를 이용해서 잘 구해야 된다...


r을 t에 대해서 1번 미분한 값이 상수 이므로 한번 더 미분하면 0이 된다.
각도 t에 대한 식으로 주어졌고, z도 t에 대한 식으로 주어졌으니 다 구할 수 있다.
이제 암기한 식에 대입만 해주면 되는데 암기가 문제네요 ㅎㅎ...

여기서도 r, v와 a의 크기가 주어졌으므로 이것을 잘 써먹어야 한다.

아 저기 r = 0.3인데 오류가 있었습니다.
있는 것을 활용해서 r에 대한 식을 구하고, v가 어떻게 이루어지는 지를 활용해 또 theta의 변화량을 구할 수 있습니다.
그렇게 하나하나 구하다 보면 전부 구할 수 있습니다.
Dependent Motion of Two particles - 두 질점의 절대 종속 운동
캐이블로 이어진 두 물체는 항상 종속적(dependent)이다.
그러므로 이를 활용하면 두 물체의 움직임, 속도, 가속도를 구할 수 있게 된다.



겹친 부분이 있는지, 변하는 부분이 어딘지 잘 확인해야 정확하게 풀 수 있다.



이 문제는 케이블이 두 개 이므로 식도 두 개이다.


이 문제도 식이 두 개이고, A를 2m/s으로 당기고 있다.




이 문제는 각도가 일정하지 않고, y와 x가 동시에 변하는 문제입니다.

전부 t에 관한 식으로 통일해 주고, 삼각형을 이용해 풀면 풀립니다.
Dependent Motion of Two Particles - 두 질점의 상대 운동
이제 움직이는 두 물체의 상대적인 속도, 가속도를 보게 됩니다.

기준이 뒤에 가서 B의 변화를 A가 보는 것입니다.


여러 식으로 표현이 가능합니다.

상대 가속도도 동일합니다.

여기선 코사인, 사인 법칙이 조금씩 사용되니 다시 상기하고 가기...


a를 기준으로 t의 상대 속도와 방향을 본사 => Vt/a = Vt - Va

식을 쪼개서 천천히 풀면 금방 풀린다.

여기서 중요한 점은 곡률이 있다는 것은 노말 방향도 있다는 것이다.




여기도 각도만 정리하면 식이 쉽게 정리된다.

잊지 말자
'기타' 카테고리의 다른 글
| 동역학 과제 2 (1) | 2024.09.28 |
|---|---|
| 역사와 한국의 영토 - 1주차 러일 전쟁과 한반도 (1) | 2024.09.25 |
| 동역학 정리 2주차 - 곡선 좌표계, 곡선 운동 curvilinear (1) | 2024.09.11 |
| 동역학 과제 1 (0) | 2024.09.09 |
| 동역학 정리 1주차 - 좌표계, 운동학 (1) | 2024.09.08 |