운동학 - Kinematics : 운동만 다루며, 위치, 속도, 가속도 그리고 시간의 변화를 다룬다.
운동역학 - Kinetics : 외부에서 힘이 가해졌을 때 운동학에 어떤 영향을 끼치는지
직교좌표계(Cartesian) : x,y,z 데카르트
극좌표계(Polar) : rcosθ, rsinθ
x = rcosθ
y = rsinθ
r = root(x^2 + y^2)
θ = arctan(y/x)

원통 좌표계 (Cylindrical) : Polar + height(cartesian)
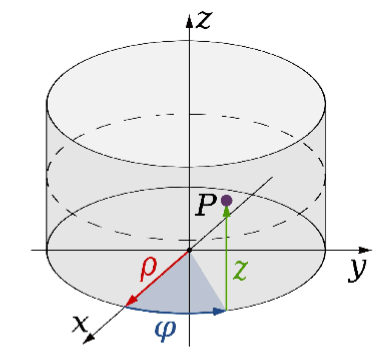
구면좌표계(Spherical) :

운동학 - 외력이 없다 == 가속도가 그대로다 -> 운동만 생각하자
좌표계 s
원점 O
지점 P
위치 벡터 r : O -> P

속도(velocity) v = ∂r / ∂t
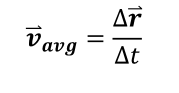
여기서 t->0 이라면 순간 속도가 된다.
속력(speed)는 |v|로 전체 이동거리를 생각해야 한다.
가속도 (Acceleration) a = ∂v / ∂t
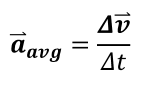
여기서 v의 대입을 통해 a를 한번 더 정의할 수 있다.
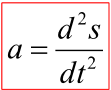
일단 여기까진 그냥 단순한 식의 전개다.

a = dv/dt 를 전개하여 적분하면 이와 같은 식이 나온다.

이 식을 통해 a에서 시간을 지우고, v를 가져올 수 있게 되었다.
이 식을 전개하면!

이러한 결과가 나오게 된다.
이 식은 진짜 처음 본 것인지 기억이 안나는데 수업 땐 왜 이렇게 되나 잘 못봤는데 지금 보니까 명확하다.

이 식은 v = ds/dt를 전개하고, v = v0 + at인 것을 이용하여 위치를 구할 수 있게 되었다.
위 식들은 전부 가속도가 일정해야지만 사용 가능하다!!
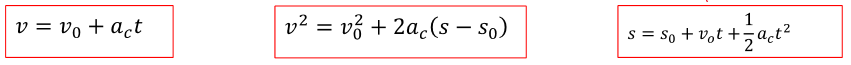
이 식 모두 가속도가 일정해야지 사용 가능한 것이다.
가속도가 일정하지 않다면!
a ds = v dv를 통해 구할 수 있다.
'기타' 카테고리의 다른 글
| 동역학 정리 2주차 - 곡선 좌표계, 곡선 운동 curvilinear (2) | 2024.09.11 |
|---|---|
| 동역학 과제 1 (0) | 2024.09.09 |
| 영어 저장소 25일차 (2) | 2024.09.06 |
| 영어 저장소 24일차 (3) | 2024.09.05 |
| 영어 저장소 23일차 (7) | 2024.09.04 |