여기서 1개 데이터마다 input으로 들어갈 차원이 D이라고 가정하겠습니다. 배치는 1이라고 생각할게요.
그럼 x는 (1,D)차원이고, 내부 hidden state는 (1,H)니까 x의 Weight는 (D,H)고, hidden state의 weight는 (H,H)겠져
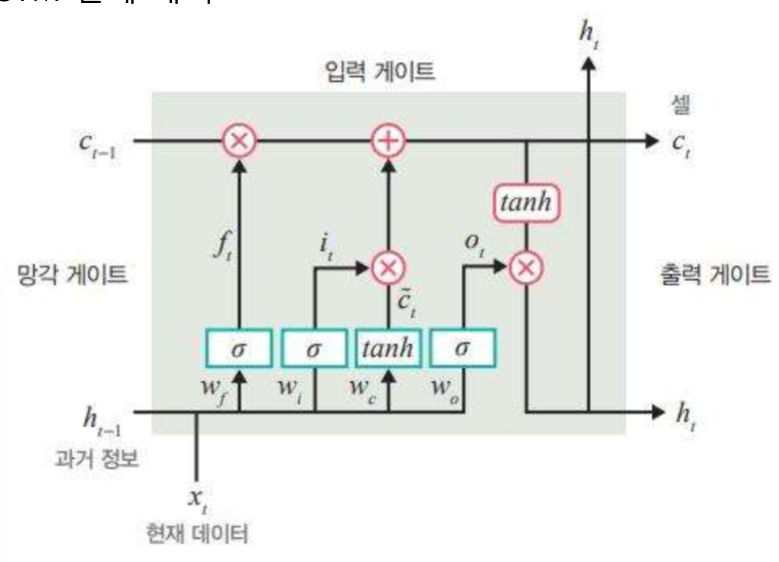
그럼 forget gate에서는 weight를 곱한 x와 hiddenstate를 더한 후 (1,H)에 Sigmoid를 통해 0~1범위로 바꾼 뒤 cell state(장기 기억) (1,H)와 각 요소끼리 곱하여(1,H) 0인 장기 기억은 버리고, 1인 장기 기억은 가지고 갑니다.
input gate에서는 또 다른 Weight를 곱한 x와 hiddenstate를 더한 후 sigmoid를 취한 것과
또 다른 Weight를 곱한 x와 hiddenstate를 더한 후 (1,H) tanh를 취한 것을 각 요소 끼리 곱하여 (1,H) cell state인 c와 더해서 새로운 정보를 추가해줍니다.
Sigmoid는 정보를 전달할지 안할지 정하고, tanh는 과거와 현재 정보를 합칩니다.
그럼 이렇게 되면 장기 기억이 완료됩니다.
output gate는 과거 데이터와 현재 데이터, 장기 기억 모두가 섞이게 됩니다.
동일하게 w와 h에 가중치 곱하고 sigmoid를 취한 뒤 장기기억에 tanh하여 곱하면 output과 다음 시점에서 사용할 hidden state가 생성됩니다.
Sigmoid는 장기 기억의 어느 부분을 출력할지 정하고, tanh는 출력할 정보의 양을 조절(압축)한다.
결국 인풋만 (1,D)고 내부와 출력은 전부 (1,H)입니다.
만약 배치 size가 B라면 x는 (B,D) hiddenstate는 (B,H)가 됩니다.
weight도 각각 곱하기 귀찮으니까 x의 weight는 (D,4H)로 곱하고, h는 (H,4H)로 곱해주면 다 따로 안하고 한꺼번에도 가능합니다.

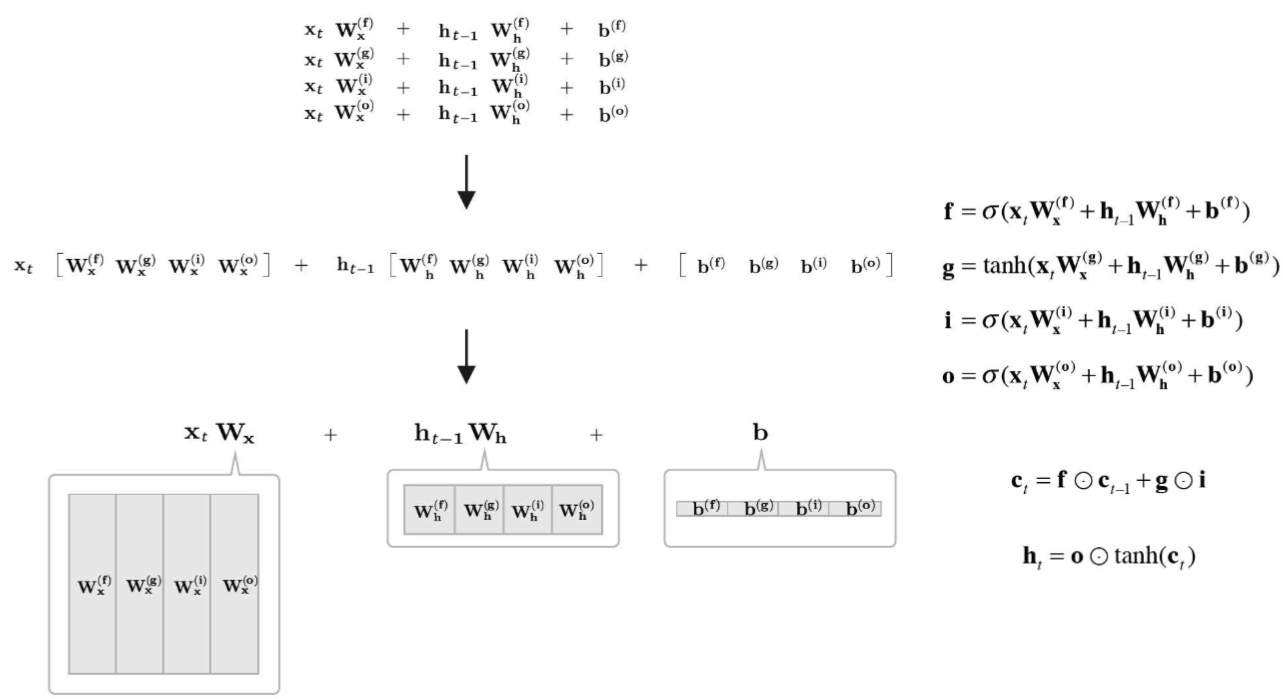
b는 (H) 차원으로 다 더해줍니다.
(N,D) (D, H) + (N,H)(H,H) -> (N,H)

그럼 여기도 결국 똑같이 (N,D)의 입력이 들오면 Weight를 통해 (N,H)로 바꿔주고 hiddenstate(N,H)와의 연산으로 이어지겠네요
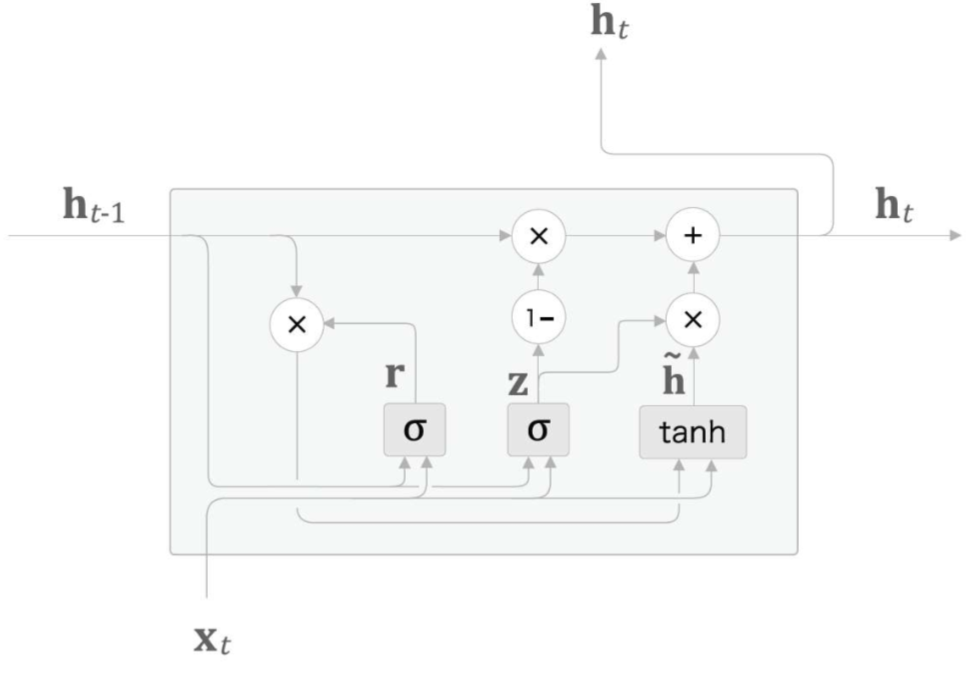
reset gate는 똑같이 Sigmoid를 통해 지울 정보를 0으로 보내는 r을 만듭니다.
그래서 이 정보를 h와 곱하고 x와의 sigmoid를 통해 새로운 정보인 h'를 만듭니다.
update gate 또한 똑같이 Sigmoid를 통해 z를 만듭니다.
그리하여 z와 h'을 요소 곱하고, 이전의 h와 (1-z)를 요소곱하여 더해 output과 다음에 전해줄 기억인 최종 h를 만듭니다.
'인공지능 > 공부' 카테고리의 다른 글
| 인공지능과 빅데이터 문제 만들기 (0) | 2024.06.21 |
|---|---|
| 인공지능과 빅데이터 11 ~ 15주차 정리 (0) | 2024.06.20 |
| 인공지능과 빅데이터 6~7, 9~10주 차 정리 (1) | 2024.06.17 |
| 생성형 인공지능 입문 기말고사 간단 정리 (1) | 2024.06.16 |
| 생성형 인공지능 기말고사 대비 문제만들기 (2) | 2024.06.15 |