2023.11.30 - [인공지능/공부] - 센서신호, FFT, STFT data를 통해 하중 예측하기
센서신호, FFT, STFT data를 통해 하중 예측하기
import tensorflow as tf import numpy as np import pandas as pd from keras.datasets.mnist import load_data from keras.models import Sequential, Model from keras.layers import Dense, Input ,Flatten, Dropout, Conv2D, MaxPooling2D, GlobalAveragePooling2D,Conv1
yoonschallenge.tistory.com
아직 RNN에 대해 정확히 공부하지 않아 확실한 사용법은 모르겠으나 일단 써보고 공부해보기로 한다.
input_2d = tf.keras.Input(shape=(1836, 100, 1))
x = tf.keras.layers.Conv2D(32, (3, 3), activation='relu', padding = 'same')(input_2d)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(64, (3, 3), activation='relu', padding = 'same')(x)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(128, (3, 3), activation='relu', padding = 'same')(x)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(256, (3, 3), activation='relu', padding = 'same')(x)
x = GlobalAveragePooling2D()(x)
x = tf.keras.Model(inputs=input_2d, outputs=x)
# 1D 데이터(예: 벡터)를 위한 입력 경로
input_1d = tf.keras.Input(shape=(10001,1))
y = LSTM(36, return_sequences=True)(input_1d)
y = LSTM(64, return_sequences=True)(y)
y = LSTM(128)(y) # 마지막 LSTM 층에서는 return_sequences를 False로 설정 (기본값)
y = tf.keras.Model(inputs=input_1d, outputs=y)
input_scalar = tf.keras.Input(shape=(3504,1))
z = LSTM(36, return_sequences=True)(input_scalar)
z = LSTM(64, return_sequences=True)(z)
z = LSTM(128)(z) # 마지막 LSTM 층에서는 return_sequences를 False로 설정 (기본값)
z = tf.keras.Model(inputs=input_scalar, outputs=z)
# 두 경로의 결합
combined = tf.keras.layers.concatenate([x.output, y.output, z.output])
# 추가 레이어 및 최종 예측 레이어
final_layer = tf.keras.layers.Dense(128, activation='relu', kernel_regularizer = l2(0.05))(combined)
final_layer = Dropout (0.2)(final_layer)
final_layer = tf.keras.layers.Dense(64, activation='relu', kernel_regularizer = l2(0.05))(final_layer)
final_layer = Dropout (0.2)(final_layer)
final_layer = tf.keras.layers.Dense(32, activation='relu', kernel_regularizer = l2(0.05))(final_layer)
final_output = tf.keras.layers.Dense(1)(final_layer) # 예: 이진 분류 문제
# 최종 모델
model = tf.keras.Model(inputs=[x.input, y.input, z.input], outputs=final_output)
# 모델 컴파일
model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate = 0.001), loss='mse', metrics=[r_squared])모델의 모양은 이렇게 나왔다. 일단 써보고 판단해보자 인데 에폭 한번에 100초 정도 걸린다..

이렇게 한 시간이 넘도록 학습하여 밑의 결과를 얻었다.


오버피팅은 확실하게 났지만 validation이 최저일 때의 결과는 그래도 예측을 많이 따라간 것을 볼 수 있다. r^2 = 0.952로 0.99에는 못 미치지만 첫 시도에선 만족스러운 결과를 얻었다. 그래서 자기 직전에 좀 더 깊게 만들어서 좋은 결과를 뽑아보려고 했다.
input_2d = tf.keras.Input(shape=(1836, 100, 1))
x = tf.keras.layers.Conv2D(32, (3, 3), activation='relu', padding = 'same')(input_2d)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(64, (3, 3), activation='relu', padding = 'same')(x)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(128, (3, 3), activation='relu', padding = 'same')(x)
x = tf.keras.layers.MaxPooling2D((2, 2))(x)
x = tf.keras.layers.Conv2D(256, (3, 3), activation='relu', padding = 'same')(x)
x = tf.keras.layers.Conv2D(256, (3, 3), activation='relu', padding = 'same')(x)
x = GlobalAveragePooling2D()(x)
x = tf.keras.Model(inputs=input_2d, outputs=x)
# 1D 데이터(예: 벡터)를 위한 입력 경로
input_1d = tf.keras.Input(shape=(10001,1))
y = LSTM(36, return_sequences=True)(input_1d)
y = LSTM(64, return_sequences=True)(y)
y = LSTM(128, return_sequences=True)(y)
y = LSTM(256)(y) # 마지막 LSTM 층에서는 return_sequences를 False로 설정 (기본값)
y = tf.keras.Model(inputs=input_1d, outputs=y)
input_scalar = tf.keras.Input(shape=(3504,1))
z = LSTM(36, return_sequences=True)(input_scalar)
z = LSTM(64, return_sequences=True)(z)
z = LSTM(128, return_sequences=True)(z)
z = LSTM(256)(z) # 마지막 LSTM 층에서는 return_sequences를 False로 설정 (기본값)
z = tf.keras.Model(inputs=input_scalar, outputs=z)
# 두 경로의 결합
combined = tf.keras.layers.concatenate([x.output, y.output, z.output])
# 추가 레이어 및 최종 예측 레이어
final_layer = tf.keras.layers.Dense(128, activation='relu', kernel_regularizer = l2(0.05))(combined)
final_layer = Dropout (0.2)(final_layer)
final_layer = tf.keras.layers.Dense(64, activation='relu', kernel_regularizer = l2(0.05))(final_layer)
final_layer = Dropout (0.2)(final_layer)
final_layer = tf.keras.layers.Dense(32, activation='relu', kernel_regularizer = l2(0.05))(final_layer)
final_output = tf.keras.layers.Dense(1)(final_layer) # 예: 이진 분류 문제
# 최종 모델
model = tf.keras.Model(inputs=[x.input, y.input, z.input], outputs=final_output)
# 모델 컴파일
model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate = 0.001), loss='mse', metrics=[r_squared])
RNN은 모델이 깊어질 수록 확실하게 학습시간이 오래걸렸다. 1 에폭에 150초가 걸리는 것을 볼 수 있다.


언더피팅...? 이전보다는 훨씬 못 미치는 결과를 볼 수 있다. 여기서 에폭만 100번으로 늘려서도 한번 돌려놨었는데
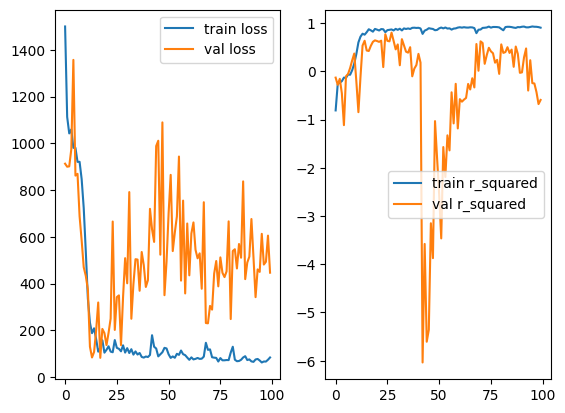

오버피팅은 오버피팅대로 나고, 결과도 만족스럽지 못했다. 다음 포스팅으론 RNN 층을 얕게 하고, RNN에 대한 학습도 들고오겠다.
'인공지능 > 공부' 카테고리의 다른 글
| 인공지능 MNIST - FCN (37) | 2023.12.01 |
|---|---|
| 센서신호, FFT, STFT data를 통해 하중 예측하기 -3 스케쥴러 (34) | 2023.11.30 |
| 센서신호, FFT, STFT data를 통해 하중 예측하기 (49) | 2023.11.30 |
| 드디어 첫 수상 (33) | 2023.11.27 |
| AI 챌린지 본선 (25) | 2023.11.24 |