Backpropagation에 대한 수식 정리는 여기서 좀 해놨었네요 ㅎㅎㅎ
2023.12.16 - [인공지능/공부] - 인공지능 backpropagation, optimization- 개념
인공지능 backpropagation, optimization- 개념
backpropagation backpropagation은 대부분의 인공지능의 파라미터 업데이트 방식이다. 우린 경사하강법을 통해 loss를 최소화 시키는 방향으로 학습한다. 기본적인 gradient 계산 방법이다. 이제 activation fun
yoonschallenge.tistory.com
단순 Back Propagation은 여기서 확인하면 되고...
2025.09.29 - [인공지능/공부] - 딥러닝 응용 1, 2 - Intro, Fundamentals 1
딥러닝 응용 1, 2 - Intro, Fundamentals 1
질병 예측과 같이 참 거짓을 나눌 수 있다.항목이 많아진다면 더 다양한 종류를 분류할 수 있음DNN(Deep Neural Networks)는 뉴런을 모방함 2 - Fundamentals 1inut xoutput yWeight wbias b or w_0Linear regression : y = w^T*
yoonschallenge.tistory.com

Stochastic Gradient descent
Loss는 MSE로 진행하고 있고, Activation function이 없는 단순한 Regression에서 Weight 업데이트 방식이다.
정답과의 오차만큼 업데이트가 진행된다. (Learning rate가 1이라면)
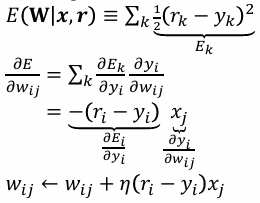
이제 출력이 여러 개가 되었다.

결국 weight 업데이트는 여러 레이어가 아니라면 동일하게 진행된다.
그러나 아래 Layer가 하나 더 있다면 겁나게 귀찮아 질듯

식에 익숙해지기

Cross entropy를 Loss로 사용하고, Activation Function으로 Sigmoid를 사용했을 때 Weight 업데이트 방법이다.
결국 소거되어 동일하게 업데이트 되는 것을 볼 수 있다.
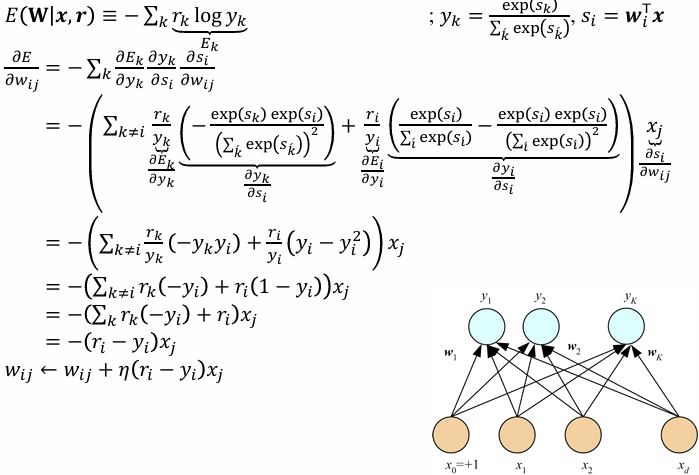
출력하는 선택지가 여러가지라 Softmax일 때 Cross entropy의 학습 방법이다.
결국 소거하다보면 동일하게 업데이트하게 된다.

수도 코드를 통해 업데이트 과정을 확인할 수 있다.
단일 Layer라서 Loss 누적은 없어 update 수식이 단순한 것을 볼 수 있다.
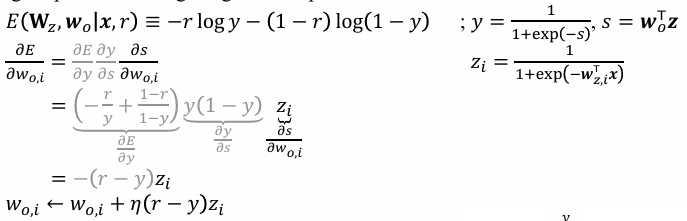
Classification은 Cross entropy 미분이니 log 미분 진행한다.
정리하면 결국 동일해지는 것 !
2025.10.03 - [인공지능/공부] - 딥러닝 응용 3 - Fundamentals 2
딥러닝 응용 3 - Fundamentals 2
Activation Functions - 다중 뉴럴 넷에 비선형성을 추가해줌기울기 소실과 같은 문제 때문에 활성 함수도 계속 진화해왔다. ELU는 또 처음 보네요 결국 Gradient 문제를 해결하거나, 다른 Activation function
yoonschallenge.tistory.com
짧게 말해:
- **MSE(Mean Squared Error)**는 특정한 손실/지표입니다.
[
\mathrm{MSE}(x,\hat x)=\frac{1}{d}\sum_{i=1}^d (x_i-\hat x_i)^2
]
연속값 데이터에 가우시안 노이즈를 가정할 때 가장 자연스러운 선택이죠. - **Reconstruction error(재구성 오차)**는 훨씬 포괄적인 개념입니다.
“원본 (x)”와 “복원 (\hat x)”의 차이를 재는 임의의 척도를 통칭합니다. 그래서 MSE도 재구성 오차의 한 종류일 뿐이고, 아래처럼 여러 선택지가 들어갑니다.
관계와 차이
- 포괄성:
- 재구성 오차 (D(x,\hat x))는 임의의 거리/발산/우도 손실을 쓸 수 있음.
- MSE는 그중 “제곱 L2 거리의 평균”이라는 특정 인스턴스.
- 통계적 해석:
- 가우시안 우도 (p(x|\hat x,\sigma^2))의 **음의 로그우도(NLL)**는
[
-\log p(x|\hat x);=;\frac{|x-\hat x|_2^2}{2\sigma^2}+ \text{const}
]
→ (\sigma^2)가 고정이면 NLL 최소화 ≡ MSE 최소화(상수 차이). - 베르누이/바이너리 데이터면 BCE, 카운트면 Poisson/Negative Binomial NLL이 더 적합—이들도 전부 “재구성 오차”의 한 형태.
- 가우시안 우도 (p(x|\hat x,\sigma^2))의 **음의 로그우도(NLL)**는
- 스케일/집계 차이:
- “reconstruction error”는 합(sum)/평균(mean)/정규화(NRMSE) 등 집계 방식까지 포함해서 말하는 경우가 많음(샘플별 임곗값으로 이상치 탐지에 쓰기도 함).
- MSE는 정의상 평균 제곱 오차.
- 도메인 맞춤:
- 이미지 품질: MSE 외에 MAE/L1, SSIM/LPIPS 같은 지각적(perceptual) 지표를 “재구성 오차”로 사용 가능.
- 오디오: SI-SDR, STFT L1/L2 등.
- 차원축소/PCA: 투영 후 잔차 (|x-\hat x|_2) 또는 분산 손실(미설명 분산)을 재구성 오차로 부름.
언제 무엇을 쓰나 (요약 가이드)
- 연속값 · 가우시안 노이즈 가정 → MSE(또는 Gaussian NLL).
- 이상치 많은 연속값 → MAE/L1 또는 Huber.
- 0/1 또는 [0,1] 확률 해석(바이너리 픽셀 등) → BCE.
- 카운트 데이터 → Poisson/NegBin NLL.
- 시각적 품질 중요 → MSE(+SSIM/LPIPS 혼합).
- 이상치 탐지(AE) → 샘플별 (D(x,\hat x))를 임계값으로 사용(지표는 MSE든 MAE든 가능).
정리: Reconstruction error는 “원본–복원 간 불일치”를 재는 개념적 우산, MSE는 그 우산 안의 대표적인 한 가지 측정/손실입니다. 선택은 데이터 타입·노이즈 모델·목표 지표에 맞춰 결정하세요.

Layer가 많은 상황에서 Batch Gradient Descent로 Epoch당 1번 파라미터 업데이트를 진행해 Local minima에 빠질 수 있다.
Stochastic Gradient Descent는 앞에 많다. 한 번 파라미터 지날 때 마다 업데이트를 진행하여 노이즈 영향 + 진동 발생 가능이 생긴다.
결국 mini-batch로 배치 크기마다 업데이트를 진행하게 된다.
Momentum - 이전 Weight에 방향성을 더해줘서 local minima에서 빠져나갈 수 있도록 해준다.

최적의 Learning rate는 이전 loss랑 지금 loss를 통해 오차를 구해서 진행
Learning late를 고정하지 않고, 스탭 별로, 진행 별로 줄이는 방식인 Decay 방식도 다양함
normalization
Batch - 한 배치에서 현재 채널의 평균과 표준편차 사용(Batch, Height와 Width)
Layer - 한 샘플의 평균과 표준 편차 사용 (Channel, Height와 Width)
Instance - 각각 샘플과 채널별로 해서 평균과 표준편차 사용 (결국 Height와 Width만 사용)
Bias - 모델이 과하게 단순함
Variance - 데이터가 바뀔 때 예측이 요동치는 정도
=> Regularization을 통해 오버 피팅 막자
2025.10.10 - [인공지능/공부] - 딥러닝 응용 4 - Architecture of DNNs
딥러닝 응용 4 - Architecture of DNNs
이미지 데이터는 공간에 대한 정보가 들어있다. 그래서 단순한 네트워크보단 순서와, 위치 정보를 파악할 수 있도록 Convolution Neural Networks를 사용해야 함 Kernel(filter), Stride, Padding을 통해 조절 하
yoonschallenge.tistory.com

RNN과 같은 Model들의 Backpropagation은 체인 룰을 통해 일어나며 연산 반복이 일어남
NAS- Neural Architecture Search를 통해 최적의 뉴럴 네트워크를 만들어 낼 수 있음
'인공지능 > 공부' 카테고리의 다른 글
| 인공지능 저작권 보호 (Copyright protection in AI) - 2 (0) | 2025.10.16 |
|---|---|
| 딥러닝 응용 9- 정리2 (0) | 2025.10.13 |
| 딥러닝 응용 7 - Large Language Models (0) | 2025.10.11 |
| 딥러닝 응용 6 - Deep Generative Models (0) | 2025.10.11 |
| 딥러닝 응용 5 - Sequence to Sequence Model (0) | 2025.10.10 |