CTC 즉 Connectionist temporal classification은 입력 길이와 출력 길이가 달라도 상관없이 학습을 가능하게 함
다음은 CTC를 “정렬 없이 라벨 시퀀스를 학습·추론”하는 방법으로 이해시키는 핵심 설명입니다.
1) CTC의 문제 설정
- 입력(프레임) 길이 (T)와 타깃 라벨 길이 (U)가 다르고, 프레임↔라벨의 정렬을 모른다.
- 네트워크는 각 시점 (t)마다 라벨 집합 (L)(예: {a,b,…})에 **블랭크 ⊔**를 추가한 (L\cup{\ ⊔\ })에 대한 확률 (y^t_k)를 출력한다.
2) “정렬이 없어도 된다”는 뜻
- 하나의 타깃 (l) 에 대해, 그 (l)로 축약되는 모든 프레임열(정렬 경로) (\pi) 의 확률을 합한다:
[
P(l\mid x,\theta)=\sum_{\pi\in\mathcal{B}^{-1}(l)}\ \prod_{t=1}^{T} y^{,t}_{\pi_t}.
]
여기서 (\mathcal{B})는 반복을 접고(blanks 제거·인접 중복 축약) 라벨열을 만드는 연산. 예:
(\mathcal{B}(,a a a ⊔ a a b b b b,)=aab).
직관: 모든 가능한 정렬을 네트워크가 “커버”하도록 확률을 모아 주니, 프레임별 라벨 위치를 사람이 달아줄 필요가 없다.
3) 초간단 수치 예시 (슬라이드 값 그대로)
타깃 (l = ab), (T=4). 시점별 소프트맥스가 아래와 같다고 하자.
[
\begin{array}{c|cccc}
& t{=}1 & 2 & 3 & 4\\hline
a: & 0.2 & 0.5 & 0.6 & 0.3\
b: & 0.1 & 0.2 & 0.3 & 0.4\
\ ⊔: & 0.7 & 0.3 & 0.2 & 0.3
\end{array}
]
(ab)로 축약되는 합법 경로 예:
① ([\ ⊔,\ a,\ ⊔,\ b]) → (0.7\cdot0.5\cdot0.2\cdot0.4=0.028)
② ([a,\ ⊔,\ b,\ ⊔]) → (0.2\cdot0.3\cdot0.3\cdot0.3=0.0054)
(P(ab\mid x)=0.028+0.0054=0.0334) (다른 경로가 있으면 더함).
블랭크가 필요한 이유: 같은 문자가 연속될 때(예: “bb”) **중간에 ⊔**가 있어야 축약 (\mathcal{B})에서 올바르게 “bb”가 남습니다.
4) 계산은 어떻게 빠르게 하나? (동적계획법)
모든 경로를 나열하지 않고, 전방/후방 변수로 합을 효율적으로 구한다.
- 타깃에 블랭크를 끼워 넣은 확장 라벨 (\hat l)을 만든다(예: ⊔a⊔b⊔).
- 전방 (\alpha_t(s)): “시간 (t)까지 (\hat l_{1:s})을 생성할 누적확률”.
경계·재귀식이 슬라이드에 제시되어 있고, 마지막에
(\ P(l\mid x)=\alpha_T(|\hat l|-1)+\alpha_T(|\hat l|)). - 후방 (\beta_t(s)) 도 유사하게 정의되며, (\beta_1(1)+\beta_1(2)=P(l\mid x)).
이로부터 CTC 손실 (\mathcal{L}=-\log P(l\mid x)) 과 미분(그라디언트)도 (\alpha,\beta)로 닫힌형식이 나온다. (프레임 (t)에서 심볼 (k)의 ‘사후확률’이 (\alpha_t\beta_t)로 계산되며 이를 이용해 역전파)
5) 학습·디코딩 관점 요약
- 학습: 미니배치마다 (P(l\mid x))를 DP로 계산 → (-\log P) 최소화.
- 디코딩:
- Greedy: 각 (t)에서 argmax 선택 후 (\mathcal{B})로 축약(빠름).
- Beam search(+언어모델): 다수 경로를 누적(정확도↑).
6) 언제 CTC가 유리한가
- 정렬 정보가 없고 입력이 더 긴 과제(ASR, 온라인 필기, 키포인트 시퀀스 등).
- 모노토닉 정렬(왼→오) 가정이 자연스러운 경우. (자유로운 재배치가 필요한 번역 등은 어텐션/트랜스포머가 보통 더 적합)
한 줄 정리
CTC는 모든 유효 정렬의 확률을 합산해 라벨 시퀀스의 우도를 계산하고, 이를 전방·후방 DP로 효율적으로 학습하는 방식입니다. 그래서 프레임 레벨 정답 정렬이 없어도 시퀀스 인식이 가능합니다.

다음 슬라이드는 CTC의 전방변수(Forward variable) (\alpha_t(s)) 를 어떻게 정의·계산하는지 보여줍니다. 핵심만 단계별로 풀어 설명할게요.
1) 상태(index (s))는 무엇인가?
- 타깃 라벨열 (l=\text{CAT})에 블랭크(⊔) 를 끼워 만든 확장 라벨열 (\hat l=\ \text{⊔ C ⊔ A ⊔ T ⊔})를 사용합니다. 각 (s)는 (\hat l) 안의 위치(심볼)를 뜻해요.
- (\alpha_t(s)) = “시간 (t)까지 (\hat l_{1:s}) 접두사를 생성했을 누적확률”입니다.
2) 초기값(베이스 케이스)
- 첫 프레임에서는 맨 위(⊔) 나 그 다음(첫 라벨) 만 도달 가능합니다:
- (\alpha_1(1)=y^1_{\text{⊔}}), (\alpha_1(2)=y^1_{\hat l_2})
- 그 외 (s>2)는 0.
3) 재귀식(전방 전개)
시간 (t)의 상태 (s)는 이전 프레임의 3개 위치에서 올 수 있습니다:
[
\alpha_t(s)=
\begin{cases}
\big(\alpha_{t-1}(s)+\alpha_{t-1}(s-1)\big);y^t_{\hat l_s}, & \text{if }\hat l_s=\text{⊔}\ \text{or }\hat l_{s-2}=\hat l_s[4pt]
\big(\alpha_{t-1}(s)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s-2)\big);y^t_{\hat l_s}, & \text{otherwise.}
\end{cases}
]
- 의미
- (s\leftarrow s) : 같은 심볼을 유지(repeat)
- (s\leftarrow s-1) : 다음 심볼로 한 칸 전진
- (s\leftarrow s-2) : (허용될 때) 블랭크를 건너뛰어 두 칸 전진
- 단, 현재 심볼이 ⊔ 이거나 (s)와 (s-2)의 심볼이 같을 때는 (s-2) 점프를 막습니다. 이유는 중복 라벨을 블랭크 없이 합쳐 버리는 불법 정렬을 방지하려는 것(예: “bb”는 중간에 ⊔가 있어야 두 개로 인정).
4) 불가능 상태 가지치기
- 남은 시간 ((T-t)) 안에 (\hat l)의 끝까지 절대 도달할 수 없는 너무 “초기” 상태는 0으로 둡니다:
[
\alpha_t(s)=0\quad\text{for } s<|\hat l|-2(T-t)-1.
]
직관: 한 타임스텝에 최대 두 칸(라벨↔블랭크) 까지만 전진할 수 있으니, 남은 칸 수가 너무 많으면 그 상태는 이미 사망(dead) 입니다.
5) 최종 우도
- 마지막 프레임 (T)에서 끝에서 한 칸((|\hat l|-1)) 또는 끝칸((|\hat l|)) 에 도달한 누적확률을 합하면,
[
P(l\mid x,\theta)=\alpha_T(|\hat l|-1)+\alpha_T(|\hat l|).
]
(확장 라벨이 마지막에 ⊔로 끝나기 때문에 두 위치 모두 허용됨.)
6) 그림(아래 DAG)의 화살표는?
- 각 열은 시간 (t), 각 행의 노드는 (\hat l)의 위치 (s)입니다.
- 화살표가 곧 허용된 전이(유지·한 칸·두 칸 전진)를 나타냅니다. 검은 노드는 해당 시점에 도달 가능한 상태의 예시입니다. (예제로 (l=)CAT 사용)
한 줄 정리
(\alpha_t(s))는 “시간 (t)에 (\hat l)의 (s)번째 심볼까지 읽어온 누적확률”. 초기값→재귀식→가지치기→마지막 두 상태 합으로 (P(l\mid x))를 얻습니다. 이 동적계획 덕분에 모든 정렬 경로를 효율적으로 합산할 수 있습니다.
좋아요. CTC에서 블랭크(⊔) 가 꼭 필요한 이유를 “무엇을 해결하느냐” 관점으로 딱 정리해볼게요.
한 줄 요약
블랭크는 ‘이 프레임에서는 라벨을 내지 않는다’(stay)라는 기호입니다.
그래서 (1) 출력 길이를 입력보다 짧게 만들 수 있고, (2) 같은 문자가 연속될 때 경계를 표시해 줍니다. 이 두 가지가 없으면 CTC가 제대로 작동하지 않습니다.
왜 꼭 필요해? (핵심 4가지)
- 프레임마다 라벨을 강제하지 않기 위해
입력 프레임 수가 (T), 라벨 길이가 (U \le T)일 때, 많이 남는 프레임들은 “라벨 없음”으로 지나가야 합니다.
→ ⊔가 없으면 모든 프레임이 a/b/… 같은 라벨 중 하나를 내야 해서 (U=T)가 되어버립니다. - 같은 문자의 연속을 구분하기 위해
CTC의 축약 연산 (\mathcal{B})는 인접한 같은 라벨을 한 개로 접습니다.
- 예) (\mathcal{B}(a,a,a)=a)
그럼 “aa” 같은 타깃을 어떻게 만들죠? - 해답: 중간에 ⊔를 둡니다. (\mathcal{B}(a,\underline{\ \ ⊔\ \ },a)=aa)
⊔가 경계 마커 역할을 해서 인접 중복이 “하나로 뭉개지는” 걸 막습니다.
(‘bb’, ‘lll’도 각각 (b⊔b), (l⊔l⊔l)처럼 표현)
- 지속 시간(duration) 모델링을 위해
음성·온라인필기처럼 한 라벨(음소/문자)이 여러 프레임에 걸쳐 지속됩니다.
⊔는 “라벨을 유지하며 시간만 흐르게” 하는 상태입니다.
직관적으로 CTC 디코딩은
라벨 출력(advance) vs ⊔ 출력(stay)
두 동작의 시퀀스라고 보면 됩니다.
- 효율적인 동적계획(전방·후방)과 합법 경로 정의를 위해
확장 라벨열 (\hat l = ⊔,l_1,⊔,l_2,…,⊔,l_U,⊔) 을 쓰면
- 허용 전이(유지/한 칸/두 칸 전진)가 깔끔해지고,
- 중복 라벨은 ⊔ 없이 두 칸 점프를 금지하여 불법 정렬을 막습니다.
이 규칙 덕분에 전방변수 (\alpha_t(s)) 재귀식이 성립하고, 모든 정렬 경로 합을 빠르게 계산할 수 있습니다.
10초짜리 수치 예시
타깃 “aa”, (T=3). 시점별 확률이
- (t=1: (a=0.6,\ ⊔=0.4))
- (t=2: (a=0.7,\ ⊔=0.3))
- (t=3: (a=0.5,\ ⊔=0.5))
합법 경로(일부):
- ([a,⊔,a]) → (0.6\cdot0.3\cdot0.5=0.09) → (\mathcal{B} = aa)
- ([⊔,a,a]) → (0.4\cdot0.7\cdot0.5=0.14) → (\mathcal{B} = aa)
- ([a,a,a])는 (\mathcal{B}=a)로 줄어들어 “aa”가 안 됩니다.
⊔가 없으면 “aa”를 만들 경로 자체가 사라집니다.
자주 나오는 오해 정리
- “중복을 그냥 허용하면 되지 않나?”
(\mathcal{B})가 인접 중복을 접는 규칙이라, ⊔ 없이는 “aa”가 자동으로 “a”로 축약돼 버립니다. - “⊔ 대신 다른 방법?”
이론적 대안(예: 라벨 복제, 별도 boundary 심볼 등)은 있지만, ⊔가 가장 단순하고 DP가 깔끔합니다. RNN-T 같은 변형도 blank(=no emission) 를 사용합니다.
결론
CTC의 블랭크는 길이 불일치와 반복 경계를 동시에 해결하는 필수 기호입니다.
생각을 이렇게 고정하세요:
라벨을 내보낼 때만 문자, 나머지 시간은 전부 ⊔.
그래서 “정렬 없이”도 올바른 라벨 시퀀스를 학습·추론할 수 있습니다.

좋아요. 이 슬라이드는 CTC의 후방변수(backward variable) (\beta_t(s)) 를 정의하고, 어떻게 재귀적으로 계산하는지 보여줍니다. 전방변수 (\alpha_t(s))의 “역방향 버전”이라고 보면 됩니다.
1) (\beta_t(s))란?
- 타깃 (l=\text{CAT})에 블랭크를 끼운 확장 라벨열 (\hat l=\ \text{⊔ C ⊔ A ⊔ T ⊔})을 쓰고,
(\beta_t(s))를 “시간 (t) 에서 시작해 (\hat l_{s:|\hat l|})(접미사) 를 완성할 누적확률”로 정의합니다.
2) 끝단 초기값(베이스 케이스)
- 마지막 프레임 (T)에서는 확장 라벨의 끝(⊔) 과 끝에서 하나 전(마지막 라벨) 만 도달 가능:
(\beta_T(|\hat l|)=y^{T}{\text{⊔}},\ \beta_T(|\hat l|-1)=y^{T}{\hat l_{|\hat l|-1}}); 그 외는 0.
3) 재귀식(뒤에서 앞으로 한 스텝 이동)
한 프레임 뒤((t{+}1))의 3개 위치로부터 올 수 있습니다:
[
\beta_t(s)=
\begin{cases}
\big(\beta_{t+1}(s)+\beta_{t+1}(s+1)\big),y^t_{\hat l_s}, & \hat l_s=\text{⊔}\ \text{또는}\ \hat l_{s+2}=\hat l_s [4pt]
\big(\beta_{t+1}(s)+\beta_{t+1}(s+1)+\beta_{t+1}(s+2)\big),y^t_{\hat l_s}, & \text{그 외}
\end{cases}
]
- 의미:
(s!\to!s) (유지), (s!\to!s{+}1) (한 칸 전진), (s!\to!s{+}2) (블랭크 건너 두 칸 전진)의 세 경로를 합산.
다만 현재 심볼이 ⊔ 이거나 (s)와 (s{+}2)의 심볼이 같을 때는 두 칸 전진을 금지(연속 중복을 블랭크 없이 허용하지 않음).
4) 가지치기(불가능 상태 = 0)
- 시간 (t) 시점엔 최대 (2t)칸까지만 뒤에서 앞으로 “채울” 수 있으므로 (s>2t)면 (\beta_t(s)=0).
5) 최종 우도와 (\alpha)–(\beta) 관계
- 처음 프레임에서 시작해 앞의 두 상태(⊔, 첫 라벨)에 도달한 값의 합이 전체 우도:
[
P(l|x)=\beta_1(1)+\beta_1(2).
] - 임의의 (t)에 대해
[
P(l|x)=\sum_s \frac{\alpha_t(s),\beta_t(s)}{y^t_{\hat l_s}}
]
도 성립하여, 프레임 (t)에서 심볼 (k)의 사후확률(그래디언트 계산에 쓰임)을 쉽게 얻습니다.
직관 한 줄
(\beta)는 “남은 구간을 완성할 확률”을 뒤에서 앞으로 누적하는 값입니다. 전방((\alpha))은 접두사 누적, 후방((\beta))은 접미사 누적—두 값이 만나 모든 정렬 경로의 합을 효율적으로 구성합니다.

요점만 잡아 설명할게요.
“Maximum Likelihood Training”이란?
데이터 ((x,l))가 주어졌을 때 모델이 정답 라벨 시퀀스 (l)을 낼 확률 (P(l\mid x,\theta))를 최대화(= 음의 로그를 최소화)하는 학습을 말합니다.
슬라이드 그대로 식은
[
\mathcal{L}=-\log P(l\mid x,\theta),
]
여기서 (P(l\mid x,\theta))는 CTC에서 모든 합법 정렬 경로의 확률 합으로 계산됩니다.
CTC에서의 우도와 α–β의 역할
전방/후방 변수로
[
\sum_s \frac{\alpha_t(s)\beta_t(s)}{y_{\hat l_s}^{,t}}
;=; P(l\mid x,\theta)
]
가 성립합니다. 즉, 시점 (t)에서 확장라벨 (\hat l_s)에 “머물러 있는” 모든 경로의 질량(αβ)을 모으면 전체 우도가 됩니다.
왜 “최대우도”를 쓰나?
- **정렬이 없는 문제(ASR 등)**에서, 모델 출력을 정답 시퀀스와 일치하는 모든 정렬에 걸쳐 “가중합”으로 맞추게 해 줍니다.
- 분류에서의 크로스엔트로피를 “정렬 미지” 상황으로 확장한 셈입니다(정확한 라벨 위치 대신, 모든 정렬의 합을 최대화).
미분(그래디언트) — 슬라이드 식의 의미
슬라이드의 도출식은
[
\frac{\partial \mathcal{L}}{\partial y_k^t}
=-\frac{1}{P(l\mid x,\theta)},
\frac{\partial P(l\mid x,\theta)}{\partial y_k^t}
=-\frac{1}{P(l\mid x,\theta)},
\frac{1}{(y_k^t)^2}
\sum_{s:\hat l_s=k}\alpha_t(s)\beta_t(s).
]
입니다. 이 값은 “시점 (t)에서 라벨 (k)가 정답 시퀀스를 만들게 하는 사후 질량(αβ)의 합”에 비례합니다. 그런 다음 연쇄법칙으로
[
\frac{\partial \mathcal{L}}{\partial w_{kj}}
= \frac{\partial \mathcal{L}}{\partial y_k^t}
\frac{\partial y_k^t}{\partial in_k}
\frac{\partial in_k}{\partial w_{kj}}
]
형태로 가중치까지 역전파합니다.
직관: 모델은 정답과 일치하는 정렬 경로들에 더 많은 확률을 배정하도록(αβ가 큰 곳의 (y_k^t)를 키우도록) 업데이트됩니다. Softmax 로그릿 (a_k^t) 기준으로 쓰면
(\displaystyle \frac{\partial \mathcal{L}}{\partial a_k^t}= y_k^t - p_k^t)
(여기서 (p_k^t=\frac{1}{P,y_k^t}\sum_{s:\hat l_s=k}\alpha_t(s)\beta_t(s))) 꼴이 되어 크로스엔트로피와 동일한 형태가 됩니다. (슬라이드의 ( \partial \mathcal{L}/\partial y_k^t ) 식을 연쇄법칙으로 변환하면 얻어짐.)
한 줄 정리
슬라이드의 “Maximum Likelihood Training”은 CTC 우도 (P(l|x,\theta))를 최대화(=NLL 최소화) 하는 표준 학습을 뜻하며, α–β(전방·후방) 로 계산한 사후 점유량을 사용해 정답과 일치하는 정렬 경로에 확률 질량을 끌어모으도록 그래디언트를 구성합니다.

다음 슬라이드는 어텐션 가중치 (a_{ij}) 를 만드는 여러 방식과, 분포 형태를 조절하는 정규화 기법을 정리한 페이지입니다. 기호는 (s_{i-1})=디코더 직전 상태, (h_j)=인코더 은닉상태, (e_{ij})=스코어(유사도), (a_{ij})=정규화된 어텐션입니다.
1) Content-based attention
- Additive(Bahdanau)
[
e_{ij}=\mathbf{w}^\top\tanh(\mathbf{W}s_{i-1}+\mathbf{V}h_j+\mathbf{b}),\qquad
a_{ij}=\frac{\exp(e_{ij})}{\sum_j \exp(e_{ij})}.
]
디코더 상태와 인코더 표현을 비선형 결합해 점수를 만듭니다. - Multiplicative(dot/General; Luong)
[
e_{ij}=\phi(s_{i-1})\cdot\psi(h_j),
]
선형사상 후 내적으로 점수를 계산합니다(파라미터/연산량이 작음).
2) Content + Location 하이브리드
- 이전 타임스텝의 정렬 (\alpha_{i-1}=(a_{i-1,1},\dots)) 위에 합성곱 커널 (F) 를 적용해 위치 특징을 만듭니다:
[
f_i=F*\alpha_{i-1},\qquad
e_{ij}=\mathbf{w}^\top\tanh(\mathbf{W}s_{i-1}+\mathbf{V}h_j+\mathbf{U}f_{ij}+\mathbf{b}),
]
이후 소프트맥스. 과거에 어디를 봤는지(정렬의 이동성/연속성)를 점수에 반영합니다.
3) Score normalization: 분포를 ‘뾰족/완만’하게
- Sharpening(온도↓)
[
a_{ij}=\frac{\exp(\beta e_{ij})}{\sum_j \exp(\beta e_{ij})},\quad \beta>1,
]
큰 점수를 더 키워 집중도↑(피크가 선명). - Smoothing(완만화)
[
a_{ij}=\frac{\sigma(e_{ij})}{\sum_j \sigma(e_{ij})},
]
시그모이드를 써서 꼬리가 두툼한 분포를 만들고 과도한 피킹을 완화합니다. - 로컬윈도우(하드 제한)
(\tilde h=(0,\dots,0,h_{p_i-w},\dots,h_{p_i+w},0,\dots,0))처럼
(p_i=\text{median}(\alpha_{i-1})) 주변만 보도록 윈도우를 걸 수 있습니다(스트리밍/단조 정렬에 유리).
4) Scaled dot-product (Transformer로의 연결)
- 점수에 차원 스케일을 적용해 분산을 안정화:
[
e_{ij}=\frac{\phi(s_{i-1})\cdot\psi(h_j)}{\sqrt{d}},
]
대각선 성분이 커져 소프트맥스가 지나치게 뾰족해지는 것을 방지(멀티헤드 자기어텐션의 표준).
언제 무엇을 쓰나 (실무 감각)
- Additive: 짧은 시퀀스·저차원 상태에서 강건, 파라미터는 많지만 유연.
- Multiplicative/Scaled-dot: 고차원·대규모에서 계산 효율↑, 트랜스포머 표준.
- Hybrid(Location-aware): ASR/발화처럼 정렬이 단조에 가까운 문제에서 지속적으로 왼→오 이동을 모델링할 때 효과적.
- Sharpen/Smooth/윈도우: 디코더가 어텐션 퍼짐이나 스텝 점프로 흔들릴 때 분포 모양을 컨트롤하는 안전장치.
요약: 이 슬라이드는 “점수 계산 방식(내용/위치/스케일) 과 정규화로 분포 모양 제어”라는 두 축으로 어텐션을 체계화하고 있습니다

Multi-head Attention은 이를 통해 연산량 감소 실현
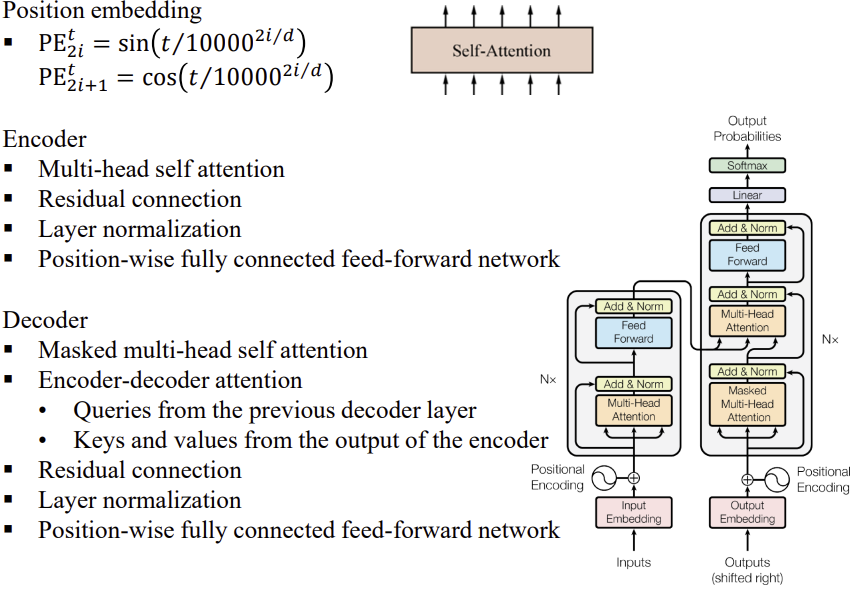
Encoder와 Decoder가 모두 있는 Transformer 구조 입니다.
Encoder의 결과가 Decoder에 Attention으로 들어가는 점이 다릅니다.
Sequence-to-Sequence Models — 핵심 요약
1) 강의 목표
- Seq2Seq 전반(CTC, Attention, Transformer)의 원리와 구현·실험 역량 확보.
2) CTC(Connectionist Temporal Classification)
- 정렬 불요: 입력 길이 (T)와 타깃 길이 (U)가 달라도 라벨 간 정렬 없이 학습.
- 블랭크(⊔)·반복 축약 연산 (\mathcal{B}) 로 모든 가능한 정렬 경로 (\pi)의 확률을 합산:
[
P(l|x,\theta)=\sum_{\pi\in \mathcal{B}^{-1}(l)}\prod_{t=1}^{T}y_{\pi_t}^{,t}.
] - 전방·후방 변수 (\alpha_t(s),\beta_t(s)) 로 동적계획법 계산 →
(;P(l|x,\theta)=\sum_s \alpha_t(s)\beta_t(s)/y^{,t}_{\hat l_s}). - 최대우도 학습: (\mathcal{L}=-\log P(l|x,\theta)), 미분식은 (\alpha,\beta)로 폐형 제공.
- 언제 쓰나: 음성·필기처럼 정렬 정보가 없고 입력이 더 긴 문제. 디코더 없이도 라벨 시퀀스 산출 가능.
3) Attention-based Encoder–Decoder (RNN 계열)
- 인코더: 양방향 RNN으로 히든 ({h_j}_{j=1}^{T_x}) 추출.
- 디코더: 시점 (i)마다 컨텍스트 (c_i=\sum_j a_{ij}h_j) 를 만들어 출력 (y_i) 예측.
- 어텐션 점수
- Additive: (e_{ij}=v^\top\tanh(Ws_{i-1}+Uh_j))
- Multiplicative: (e_{ij}=\phi(s_{i-1})!\cdot!\psi(h_j))
- (;a_{ij}=\mathrm{softmax}j(e{ij})).
- 변형: Content+Location(이전 어텐션의 합성곱 특징 (f_i) 추가), Sharpen/Smooth(스코어 스케일링 (\beta) 혹은 시그모이드 정규화).
- 장점: 길이 불일치·장거리 의존에 강함, 정렬을 함께 학습. 번역/ASR(LAS) 등 광범위.
4) Self-Attention & Transformers
- Self-Attention: 각 위치가 자신의 시퀀스에 주의
[
\text{Attn}(Q,K,V)=\mathrm{softmax}!\left(\frac{QK^\top}{\sqrt{d}}\right)V,\
q_i=W_q x_i,\ k_j=W_k x_j,\ v_j=W_v x_j.
] - Multi-Head: 서로 다른 투영으로 병렬 주의 → 결합(CONCAT) 후 (W_o).
- 포지션 인코딩: (\mathrm{PE}_t^{(2i)}=\sin(t/10000^{2i/d}),; \mathrm{PE}_t^{(2i+1)}=\cos(\cdot)).
- 인코더: (MH-SelfAttn → FFN) + Residual + LayerNorm.
- 디코더: 마스킹 SelfAttn + Encoder–Decoder Attn + FFN(각각 Residual/LN).
- 특징: 병렬 처리, 긴 의존성 처리 능력, NMT/ASR(Conformer 포함) 표준 백본.
5) 무엇을 언제 쓰나 (실전 가이드)
- CTC: 프레임-라벨 정렬 불명, 빠른 디코딩·온디바이스 선호(ASR 스트리밍).
- RNN-Attention: 중·장문 시퀀스 정렬이 중요, 데이터 중간 규모.
- Transformer: 대규모 데이터/병렬 학습, 긴 문맥·정확도 최우선. 하이브리드(CTC+Attn, Conformer)도 실무 표준.
6) 한 페이지 체크리스트
- 과제: 정렬 유무(CTC?) · 길이 비례성 · 실시간성(마스킹/스트리밍)
- 모형: Encoder(BiRNN/Conv/Transformer) · Decoder 유형(CTC/Attn)
- 어텐션: additive vs dot, multi-head 수, 위치 정보(PE/relative)
- 학습: (\mathcal{L}_{\text{CTC}}) / CE, 라벨 스무딩, 스케줄러, 샘플링(teacher forcing vs beam)
- 지표: CER/WER, BLEU, latency/FLOPs, 메모리.
원하면 위 요약을 모델 선택 플로우차트와 실험 템플릿(파이토치) 형태로 바로 만들어 드리겠습니다.
Medical References
- None
DOI: file_00000000c510620a9cb4c9739938e702
'인공지능 > 공부' 카테고리의 다른 글
| 딥러닝 응용 7 - Large Language Models (0) | 2025.10.11 |
|---|---|
| 딥러닝 응용 6 - Deep Generative Models (0) | 2025.10.11 |
| 딥러닝 응용 4 - Architecture of DNNs (0) | 2025.10.10 |
| 딥러닝 응용 3 - Fundamentals 2 (1) | 2025.10.03 |
| 딥러닝 응용 1, 2 - Intro, Fundamentals 1 (0) | 2025.09.29 |