
질병 예측과 같이 참 거짓을 나눌 수 있다.
항목이 많아진다면 더 다양한 종류를 분류할 수 있음
DNN(Deep Neural Networks)는 뉴런을 모방함
2 - Fundamentals 1
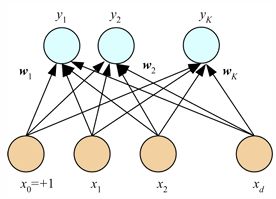
inut x
output y
Weight w
bias b or w_0
Linear regression : y = w^T*x
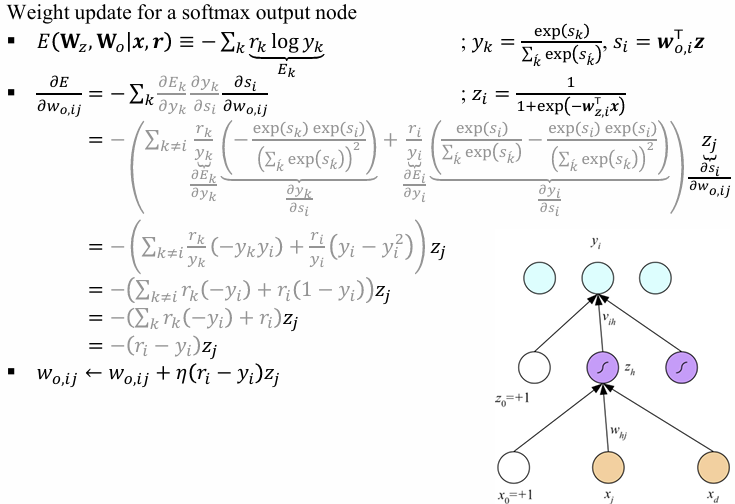
Binary classification은 threshold function을 구하는 과정이라면 Sigmoid는 확률을 출력
Multiclass classification은 Softmax를 통해 진행되며 가장 높은 값 y_k값 선택
Stochastic gradient descent
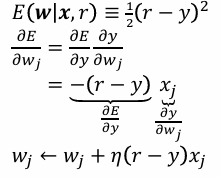
η - 학습률 (learning rate or step size)
r은 여기서 gold 즉 정답이다.
여기선 출력이 하나였는데 여러개가 된다면 w는 input 개에서 input * output 개가 된다.


다음 슬라이드는 “엔트로피–크로스엔트로피–KL”의 연결을 한 번에 정리해서, 왜 크로스엔트로피(CE) 를 손실로 쓰는지, 그것이 곧 데이터분포 (p) 와 모델분포 (q) 의 불일치(KL) 를 줄이는 일과 동치임을 보여주려는 목적입니다. 슬라이드에 나온 정의는 아래와 같습니다.
무엇이 무엇인지 (직관 + 수식)
- 엔트로피 (H(p))
- 정의: (H(p)=-\sum_x p(x)\log_2 p(x)) — 분포 (p)의 평균 불확실성/최적 부호화 길이(비트).
- 베르누이 (p(\text{1})=\theta)이면 (H(\theta)=-\theta\log_2\theta-(1-\theta)\log_2(1-\theta))로, (\theta=0.5)에서 최대(그래프가 그려진 이유).
- 크로스엔트로피 (H(p,q))
- 정의: (H(p,q)=-\sum_x p(x)\log_2 q(x)) — 진짜 분포 (p) 에서 샘플이 오는데 모델 (q) 로 부호화(또는 예측)했을 때의 평균 코스트.
- 성질: (p=q) 일 때 최소. (슬라이드는 Jensen 불등식으로 메모)
- KL 발산 (D_{\mathrm{KL}}(p\Vert q))
- 역할: (q)를 (p)로 착각할 때 생기는 추가 비용(비효율), 즉 “얼마나 틀렸는가”를 재는 비대칭 거리.
- 정의/전개:
[
D_{\mathrm{KL}}(p\Vert q)=\sum_x p(x)\log_2 \frac{p(x)}{q(x)}
= -\sum_x p(x)\log_2 q(x)+\sum_x p(x)\log_2 p(x)
= H(p,q)-H(p).
]
즉 KL = 크로스엔트로피 − 엔트로피. 슬라이드의 “식이 복잡해 보이는” 이유는 사실 이 단순한 분해(로그 비의 선형성)와 동일해서, 표기만 길 뿐입니다.
왜 이 파트가 강의에 필요한가
- 곧바로 이어지는 슬라이드에서 시그모이드/소프트맥스 출력의 손실로 CE 를 쓰고, 그라디언트가 ((r-y)) 꼴로 깔끔하게 떨어짐을 유도합니다. 이는 CE 최소화 ≡ (D_{\mathrm{KL}}(p\Vert q_\theta)) 최소화(상수 (H(p)) 제외)라는 이론적 배경 덕분입니다.
실전적 해석(연구/구현 관점)
- 분류 학습(MLE): 경험적 CE를 줄이는 것은 (p_{\text{data}})와 (q_\theta)의 KL을 줄이는 일—즉 모델이 데이터 분포를 닮아가게 만듭니다.
- 정규화/제약: VAE의 ELBO, 정책최적화(PPO)의 KL 패널티, 지식증류(teacher–student) 등은 KL을 직접 항으로 사용해 “멀어지지 않게” 조절합니다.
- 단위: (\log)의 밑이 2면 bits, (e)면 nats—수치만 스케일이 다르고 의미는 동일.
빠른 직관 예시
동전의 진짜 앞면확률이 (p(1)=0.9)인데 모델이 (q(1)=0.6)이라면, (D_{\mathrm{KL}}(p\Vert q))는 “그 틀린 모델로 코딩/예측할 때 생기는 여분의 비트 수”를 의미합니다. 극단 확률(0.9 vs 0.6)에서의 불일치가 클수록 KL이 급격히 커집니다(안전·정확성 관점에서 왜 KL을 중시하는지 직관).
요약하면, 엔트로피는 “내재 불확실성”, 크로스엔트로피는 “(p)를 (q)로 기술할 때의 비용”, KL은 그 둘의 차이인 “모델의 비효율(불일치)”입니다. 그래서 분류에서 CE를 최소화하면 자동으로 KL을 줄이는 것이고, 그게 바로 이 파트가 손실함수 도입 직전에 배치된 이유입니다.
위 식(Cross Entropy)을 Loss로 활용하여 학습할 때 결국 동일한 weight 업데이트 량을 볼 수 있다.
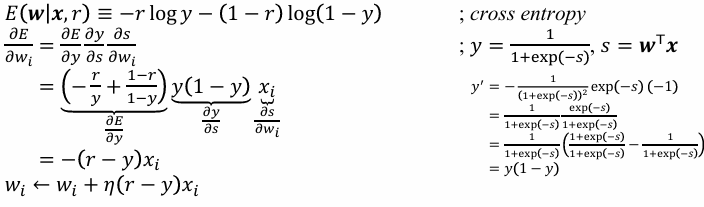

Multi Node 상황에서도 동일할 결과가 나옴을 볼 수 있다.

수도 코드로 확인 가능하다.
단일 퍼셉트론은 and를 표현할 수 있지만 XOR을 표현할 수 없다.
2층이 되어야 한다
=> Multilayer Perceptrons
- Hidden layer 의 node 들은 z로 표현

기존 Regression task의 경사 하강법

출력 직전인 Hidden layer의 경사하강
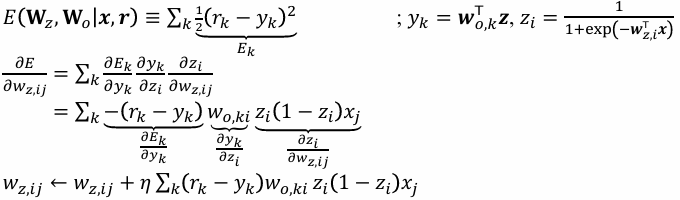
다음 Layer의 업데이트

SGD
이젠 Classification의 update를 진행한다.

Loss function은 바뀌었으나 update 방식은 동일하다.
좋은 질문입니다. 겉보기엔 업데이트가 늘
(\Delta w = \eta,(r-y),x) 꼴로 비슷해 보이지만, 손실은 학습의 통계적 가정·기하·최적화 동역학을 완전히 바꿉니다. 그래서 과제/데이터 특성에 맞춰 서로 다른 손실을 쓰는 겁니다.
왜 손실을 바꾸는가 (핵심 포인트)
- 통계적 가정(노이즈 모델)이 다르다
- MSE ↔ Gaussian 노이즈 가정(연속값 평균 예측).
- CE(시그모이드/소프트맥스) ↔ Bernoulli/Categorical 가정(확률 예측).
- Poisson NLL ↔ 카운트 데이터.
⇒ 같은 ((r-y)) 모양의 신호라도 “무엇을 맞추려는가(평균/확률/카운트)”가 달라집니다.
- 기하와 곡률(헤시안)이 달라서 학습 동역학이 달라진다
- 시그모이드+MSE: (\partial L/\partial s=(y-r),y(1-y)) → 포화 구간에서 그라디언트가 거의 0.
- 시그모이드+CE: (\partial L/\partial s=(y-r)) → 틀렸을수록 큰 신호가 남아 빠르게 교정.
⇒ 업데이트 형태는 비슷해 보여도 스케일·곡률이 달라 수렴 속도와 안정성이 크게 다릅니다.
- 평가 지표와의 정렬(what you optimize is what you get)
- 확률 보정(calibration) 이 중요하면 CE(로그우도)가 적합(‘proper scoring rule’).
- 마진이 중요하면 Hinge/ArcFace류(결정경계 간격 극대화).
- 랭킹/AUC이면 pairwise/logistic-랭킹, LambdaRank 등.
- 견고성·데이터 편향 대응
- 이상치 많은 회귀 → L1/Huber(로버스트).
- 클래스 불균형/쉬운 음성 과다 → Focal loss 또는 가중 CE.
- 라벨 노이즈 → 라벨 스무딩/대칭 CE 등.
- 불확실성/분포 예측이 목표일 때
- 헤테로스케다스틱 회귀: Gaussian NLL로 (\mu,\sigma) 동시 예측(분산까지 학습).
- 카운트의 과산포 → Negative Binomial NLL.
⇒ 단순 평균이 아니라 분포 자체를 맞춥니다.
- 표현학습/자기지도
- InfoNCE, Triplet/BPR, Barlow Twins, VICReg 등은 관계(유사도/상관) 를 직접 최적화해, 분류용 CE와 전혀 다른 표현을 끌어냅니다.
“업데이트가 비슷한데 왜 결과가 다르지?” (짧은 해부)
- 1차식만 보면 ((r-y))가 흔하지만, (i) 링크함수, (ii) 손실의 곡률(헤시안/Fisher), (iii) 샘플별 스케일링 이 달라 경로·속도·최종 해가 달라집니다.
- 예: 잘못된 확신( (y\approx 0) 인데 정답 1) 에서 CE는 큰 그라디언트, MSE는 (y(1-y)) 때문에 작은 그라디언트 → CE가 분류에서 훨씬 잘 수렴.
무엇을 언제 쓰나 (실전 미니 가이드)
- 실수 회귀(평균): MSE; 이상치 많음 → Huber/L1; 분산도 예측 → Gaussian NLL((\mu,\sigma)).
- 이진/다중 분류(확률): CE(+가중/Focal/라벨스무딩); 마진 중요 → Hinge/ArcFace.
- 랭킹/추천: Pairwise logistic/BPR, LambdaRank.
- 세그멘테이션: CE + Dice/IoU(Tversky) 혼합(심한 불균형 대응).
- 카운트·시간당 사건수: Poisson/NegBin NLL.
- 자기지도/대조학습: InfoNCE/NT-Xent, Triplet.
요약: 업데이트 식이 비슷해 보이는 것은 특정 조합(지수족+정준 링크)에서 나타나는 표면적 현상일 뿐, 손실은 모델이 믿는 세계·학습의 기하·지표 정렬·견고성을 결정합니다. 문제의 본질과 데이터 특성, 최종 목표 지표에 맞춰 손실을 설계·선택하는 것이 성능과 안정성의 핵심입니다.

이제 Multinode Classification으로 softmax를 활용한다.



DNN - Deep Neural Networks
위에서 진행했던 것을 여러 레이어에서 반복하여 진행합니다.
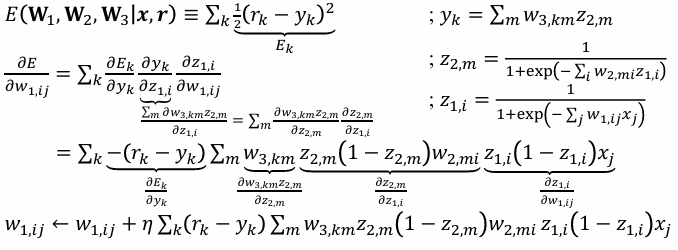
시간 복잡도는 O(n^L)이다. Layer가 많아질수록 기하 급수적으로 늘어나버린다.


Autoencoder인 Encoder와 Decoder 구조로 입력과 출력을 동일하게 만들 수 있다.
Denoising, Sparse(input < hidden dimension), Deep, stacked 등 다양하게 진화
Representation 학습으로 인해 Embedding 등 다양하게 생성 가능
1) 강의 목표
- 딥러닝의 정의와 이론·응용 이해
- AI, ML, DL 구분 능력 함양
- 최신 논문 실험 재현 및 성능 개선, 단문 연구보고서 작성 능력 달성
2) 핵심 개념 정리
인공지능(AI)
- 정의(맥카시 1956): 지능의 모든 측면을 기계적으로 모사할 수 있다는 가정 하에, 언어 사용·추상화·문제해결·자기개선을 기계가 수행하도록 만드는 과학·공학.
- 네 가지 관점: 인간적으로/합리적으로 × 생각/행동(투링 테스트, 인지모형, 사고의 법칙, 합리적 에이전트).
- 분야: 상태공간 탐색, 추론, 지식표현, 계획, 머신러닝, 지각, 감성컴퓨팅, 창의성, AGI/ASI.
머신러닝(ML)
- 정의: 데이터의 패턴을 자동 학습해 미래를 예측/기술; 매개변수화된 모델을 훈련 데이터로 최적화.
- 유형: 지도(분류/회귀), 비지도, 강화, 반지도(셀프트레이닝/약지도), 자기지도(표현학습).
- 왜 필요한가: 인간 지식 부재/설명 불가, 환경/해의 변화, 개인화 필요, 데이터 풍부·지식 희소.
딥러닝(DL)
- 정의: 조정 가능한 연결 강도를 가진 복잡한 대수적 회로(인공신경망, DNN) 기반의 ML 기법군.
- 역사 스냅샷: 뉴런 모델(1943) → AI 탄생(1956) → 초기 낙관/비판 → 전문가시스템 → ANN의 귀환(1986–) → 빅데이터(2001–) → 딥러닝(2011–).
- 응용: 게임, 이미지/음성, 번역, 자율주행, 로보틱스.
3) 대표 커뮤니티
- 컨퍼런스: NeurIPS, ICLR, ICML, AAAI, IJCAI, CVPR, Interspeech, ICASSP/ASRU/SLT, ACL/NAACL/EMNLP 등.
- 저널: TNNLS, TPAMI, TASLP 등.
4) 최근 연구 주제(샘플)
- 적응: LoRA (ICLR 2022)
- ICL: 데모의 역할 재고(EMNLP 2022)
- 신뢰도/콘피던스, ASR 오류 보정(FastCorrect2 등)
- LLM×음성: 디코더-온리 S2T 통합(ASRU 2023), SALMONN(ICLR 2024), LLM 프롬프팅(ICASS P 2024)
- 비/반지도 ASR: 불확실성 기반 자기학습, CycleGAN, 약지도 학습 등.
Deep Learning Fundamentals I — 체계적 요약
1) 강의 목표
- 딥러닝의 기초 수학·알고리즘(퍼셉트론, MLP, 역전파)의 원리를 이해한다.
- 주어진 응용 과제에 맞춰 기본 DNN을 직접 설계·구현한다.
2) 퍼셉트론(Perceptron)과 확률적 해석
- 단일 퍼셉트론: 입력 (x_j), 가중치 (w_j), 선형결합 (s=\mathbf{w}^\top \mathbf{x}), 출력 (y).
- 회귀: (y=s) (MSE 최적화)
- 이진분류(하드 임계값): (y=\mathbb{1}[s>0])
- 이진분류(확률): 시그모이드 (y=\sigma(s)=1/(1+e^{-s})) (CE 최적화)
- 다중 퍼셉트론(선형 다중출력): (\mathbf{y}=W\mathbf{x}) (다변량 회귀).
- 다중분류: 소프트맥스 (y_i=\exp(s_i)/\sum_k \exp(s_k)), (\ s_i=\mathbf{w}_i^\top\mathbf{x}).
- 엔트로피/교차엔트로피/KL: 손실로서의 의미와 최소화 시 (p=q) 조건 정리.
핵심 업데이트(확률적 경사하강, 한 샘플 기준)
- 선형 출력(MSE): (w_j \leftarrow w_j+\eta(r-y),x_j)
- 시그모이드(CE): (w_j \leftarrow w_j+\eta(r-y),x_j) (미분 결과가 동일 형태)
- 소프트맥스(CE): (w_{ij}\leftarrow w_{ij}+\eta(r_i-y_i),x_j)
3) 다중 퍼셉트론의 한계와 XOR
- AND는 선형 분리가 가능하지만 XOR는 단층으로 분리 불가 →
두 층(은닉 비선형)으로 “합의 논리합(Disjunction of Conjunctions)”로 표현 가능. - 비선형 은닉층의 중요성: 은닉이 선형이면 ( \mathbf{y}=V(W\mathbf{x})=U\mathbf{x}) 로 단층과 동치.
- 보편 근사 정리(UAT): 적절한 비선형·은닉수로 연속함수를 임의의 정확도로 근사 가능.
4) 다층 퍼셉트론(MLP) 구조와 순전파
- 입력 ( \mathbf{x}) → 은닉 ( \mathbf{z}=\sigma(W_z\mathbf{x})) → 출력
- 회귀: ( \mathbf{y}=W_o\mathbf{z})
- 분류: 시그모이드/소프트맥스 출력
- 의사결정 영역 예시와 표현학습 관점 소개.
5) 역전파(Backpropagation) 핵심 정리
출력층 그라디언트(대표형)
- 회귀(MSE): ( \delta_i = r_i - y_i,\ \ \Delta w_{ij} = \eta,\delta_i,z_j )
- 이진(시그모이드+CE): ( \delta = r - y,\ \ \Delta w_i = \eta,\delta, z_i )
- 다중(소프트맥스+CE): ( \delta_i = r_i - y_i,\ \ \Delta w_{ij} = \eta,\delta_i, z_j )
은닉층 그라디언트
- 한 은닉노드 (z_i):
(\delta^{(hid)}i = \big(\sum_k \delta^{(out)}*k,w^{(out)}{k i}\big), z_i(1-z_i)),
(\Delta w^{(hid)}*{ij} = \eta,\delta^{(hid)}_i, x_j). - 다중 은닉층 일반식: (\delta^{(\ell)} = \big(W^{(\ell+1)\top}\delta^{(\ell+1)}\big)\odot \sigma'(s^{(\ell)})).
- 시간복잡도(개략): (\mathcal{O}(nL)).
의사코드(요지)
- 순전파: 각 층 (s=Wz,\ z=\sigma(s)), 마지막 층에서 (y) 산출
- 출력층 (\delta) 계산(위 식)
- 뒤에서 앞으로 (\delta) 역전파, (\Delta W=\eta,\delta,z^\top) 업데이트.
6) 응용 블록
(a) 멀티라벨 분류
- K개의 독립 시그모이드 출력, 라벨 벡터 (\mathbf{r}\in{0,1}^K).
- 손실: (\sum_k -r_k\log y_k - (1-r_k)\log(1-y_k)),
업데이트: 출력 ( (r_i-y_i) z_j ), 은닉은 가중합으로 역전파.
(b) 차원축소 — 오토인코더(AE)
- 인코더 (z=\mathrm{ENC}(x;W)), 디코더 (\hat{x}=\mathrm{DEC}(z;V)),
재구성 MSE 최소화: (\frac{1}{N}\sum_t |x_t-\hat{x}_t|_2^2). - 변형: Denoising AE, Sparse AE, Deep/Stacked AE.
- 선형 AE ↔ PCA(강의 예시 흐름상 연결).
(c) MDS / Sammon 매핑
- 고차 → 저차 임베딩에서 쌍대 거리 왜곡 최소화(Sammon stress).
- MLP로 매핑 함수 (g(x|\theta)) 학습.
(d) 표현학습(Representation Learning)
- 고정 기저 (\phi(\cdot)) 대신 학습 가능한 기저 ( \phi(x;w)=\sigma(w^\top x)) 로
선형 불가능 문제(XOR 등)를 선형화 가능한 새 공간에서 풀도록 함. - 전이·다중과제·자기지도 → 대규모 비지도 사전학습 + 소규모 지도 미세조정.
(e) 단어 임베딩(Word2Vec, Skip-gram 개요)
- 윈도우 문맥 → 중심어 예측(출력 원-핫).
- 연속벡터 공간에서의 의미 연산(“Paris − French + London ≈ English”).
7) 실전 체크리스트(연구·구현 관점)
- 손실 선택: 분류는 CE(+소프트맥스/시그모이드), 회귀는 MSE.
- 라벨 체계: 멀티클래스(원-핫+소프트맥스) vs 멀티라벨(시그모이드 K개).
- 학습 안정화: 작은 난수 초기화, 학습률 스케줄, 셔플, 조기종료.
- 그라디언트 소실 대응: 비선형 포화 구간 회피(실무에선 ReLU류/정규화 활용).
- 표현 재사용: AE/자기지도 임베딩을 다운스트림에 전이.
8) 한 페이지 치트시트
- 업데이트 규칙 요약
- Linear/MSE: (\Delta w_{ij}=\eta(r_i-y_i),z_j)
- Sigmoid+CE: (\Delta w_i=\eta(r-y),z_i)
- Softmax+CE: (\Delta w_{ij}=\eta(r_i-y_i),z_j)
- Hidden: (\Delta w_{ij}=\eta\big(\sum_k\delta_k w^{\text{next}}_{k i}\big),z_i(1-z_i),x_j)
- 역전파 골격: Forward → 출력 δ → 층별 δ 역전파 → 가중치 갱신.
'인공지능 > 공부' 카테고리의 다른 글
| 딥러닝 응용 4 - Architecture of DNNs (0) | 2025.10.10 |
|---|---|
| 딥러닝 응용 3 - Fundamentals 2 (1) | 2025.10.03 |
| Training LLMs to be Better Text Embedders through Bidirectional Reconstruction 코드 까보기 (0) | 2025.09.25 |
| 딥러닝 응용 - 3주차 (0) | 2025.09.15 |
| 딥러닝 응용 - 2주차 (0) | 2025.09.08 |