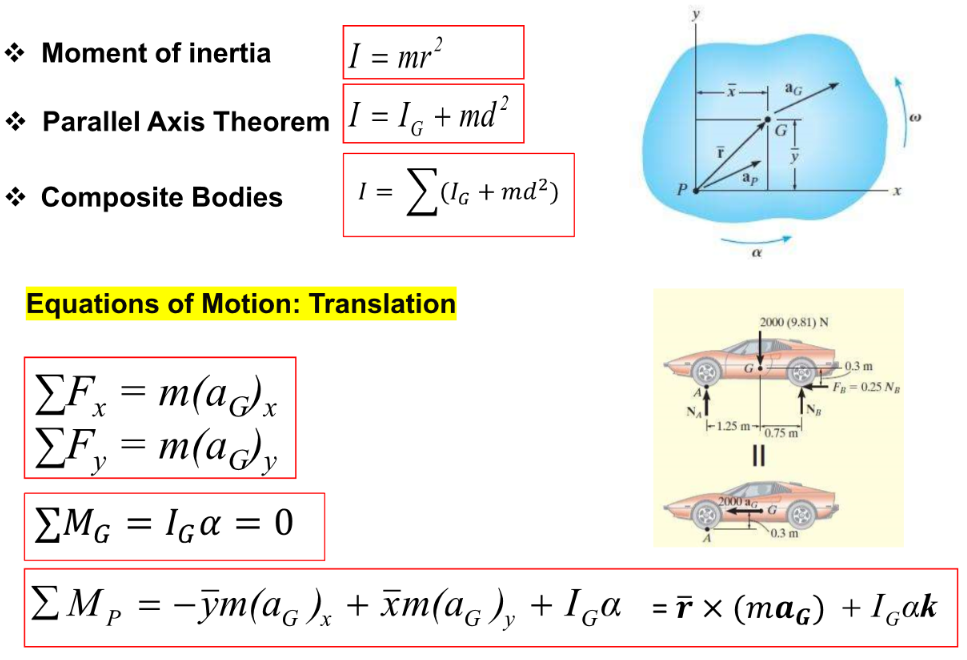
외우자
뭔가 이해가 안된다면 그냥 일단 외우기라도 하자....
더 이상 물리를 할 건 아니니까...
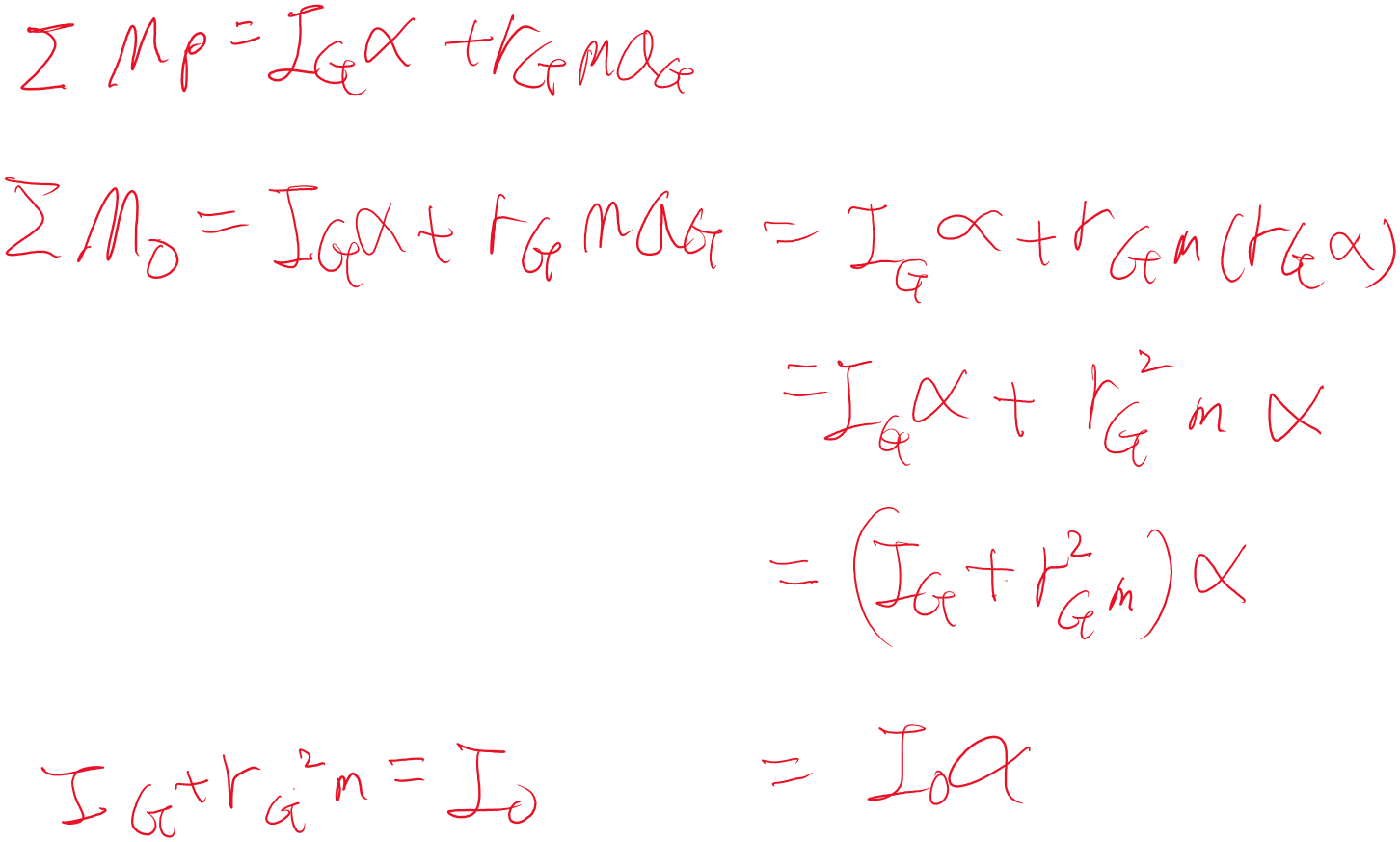
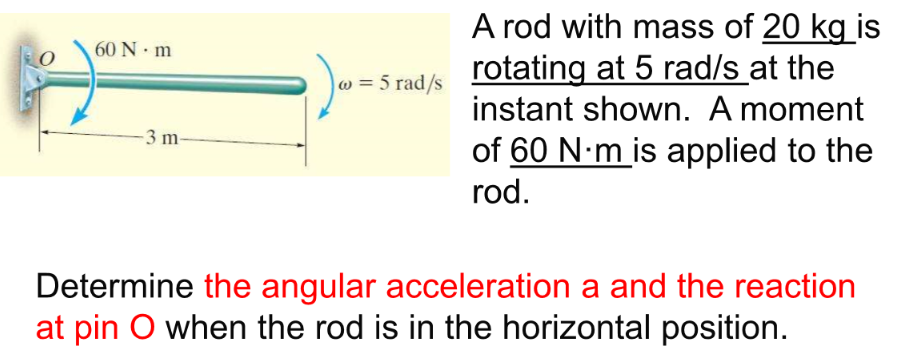
봉이 고정되어있고, 힘과 각속도 모두 주어졌네요

여기선 x,y로 나누기보다는 norm과 tangential로 나눴다.

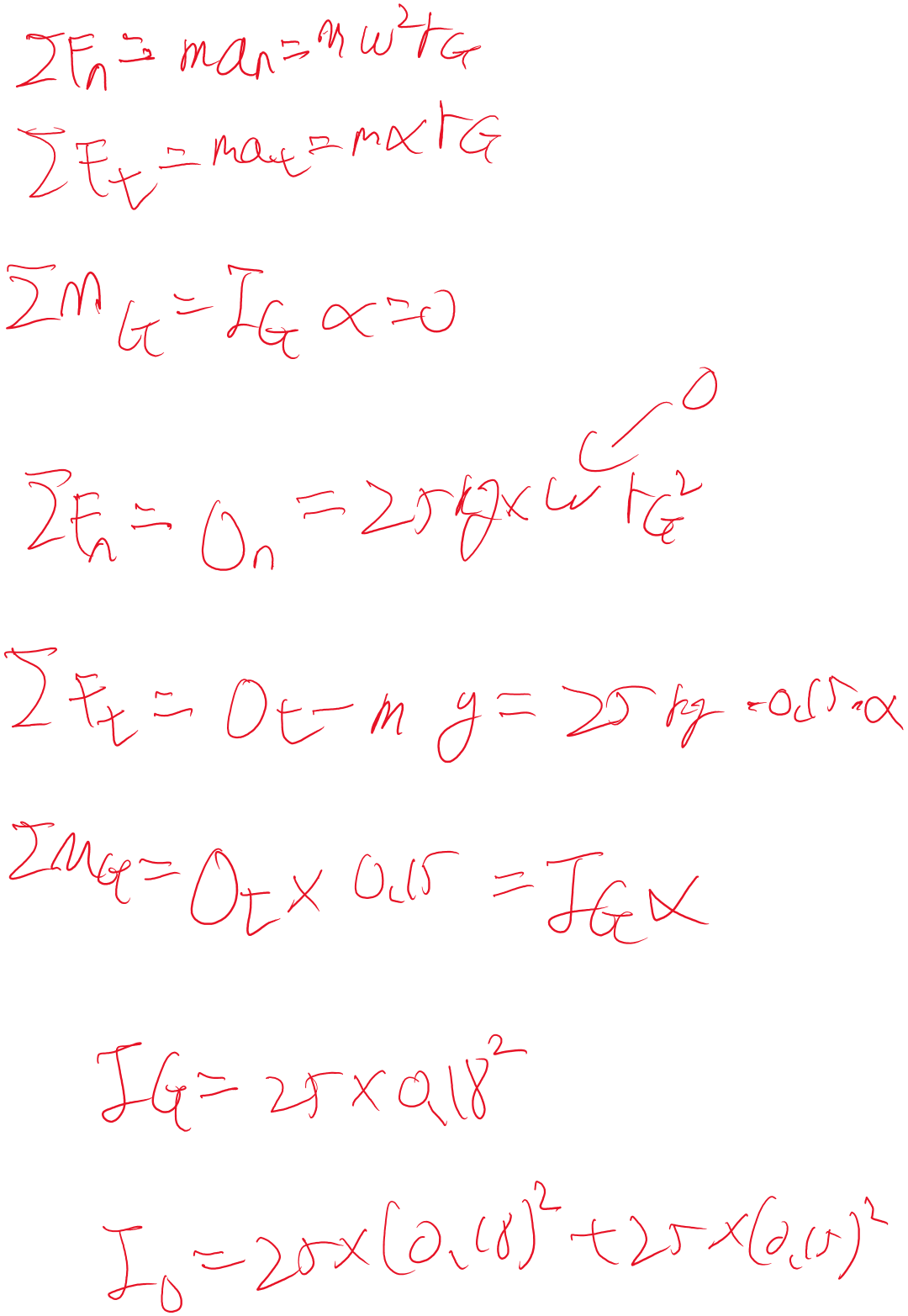

o1한테 풀어보라고 시켰는데 잘 푸네요
먼저 용어 정리를 하겠습니다. 여기서 O_t는 O점(핀)에서 원판을 잡아주는 ‘탄젠셜(tangential)’ 방향의 반력입니다. 즉, 원판의 질량중심 G의 운동 방향을 기준으로, 접선방향(tangential direction)에 작용하는 힘입니다. 이 문제에서 탄젠셜 방향이란 G가 회전하려고 할 때, 그 순간 G가 움직이려고 하는 방향(원판 둘레를 따라가는 방향, 아래쪽)으로 본 것입니다.
질문하신 핵심은 다음과 같습니다:
"축 O는 움직이지 않는데, 왜 거기서 탄젠셜 방향 반력 O_t가 0이 아닐까?"
즉, "O점이 고정되어 있다면, 그 점에서 가로든 세로든 힘이 없어도 되는 게 아닐까?"라는 의문입니다.
핵심 개념 정리:
- 고정된 점(핀)에서도 반력은 충분히 존재할 수 있습니다. 물체가 고정점 주위로 회전하거나 움직이는 것을 막거나 유도하려면, 그 고정점은 물체에 필요한 힘을 제공해야 합니다.
- “점 O가 가만히 있으니 그 점에서 반력이 0이다”는 생각은 잘못된 전제입니다. 고정점은 움직이지 않지만, 그 이유는 바닥(또는 고정된 구조물)이 충분히 강하고, 그 점이 물체에게 필요한 힘(반력)을 줘서 그 점 자체는 움직이지 않게 유지하는 것입니다. 쉽게 말해, 고정점은 물체로부터 받은 힘을 다시 지면 등으로 전달하여 반작용하는 것이므로 반력이 존재할 수밖에 없습니다.
왜 탄젠셜 힘이 필요한가?
이 상황에서 질량중심 G는 아래 방향(접선방향)으로 가속되고 있습니다. G가 아래로 가속하기 위해서는 반드시 그 방향으로 순수한 중력만 작용해서는 안 됩니다. 왜냐하면 순수 중력만 있으면 원판은 자유낙하하듯 직선으로 떨어질 텐데, 여기서는 한 점 O를 축으로 회전하는 형태의 운동을 합니다.
- 원판은 단순히 떨어지는 것이 아니라, O점을 기준으로 시계방향으로 회전하기 시작합니다.
- 회전하려면 원판에 토크(돌림힘)가 필요하고, 토크를 만들기 위해서는 O점에서의 힘들, 특히 질량중심 방향으로의 힘(접선 방향 힘)이 필요할 수 있습니다.
- 중력은 G점에서 아래로 작용하지만, O점을 중심으로 보면 이 중력은 회전시키는 토크를 유발합니다. 이제 원판은 그 토크로 인해 회전 가속도를 가지는데, 이 회전운동으로 G점이 아래쪽으로 가속하면서 움직이려면, O점에서도 그 운동을 적절히 "안내"하는 힘이 필요합니다.
좀 더 쉽게 비유해 보겠습니다:
문이 한쪽 벽에 힌지로 고정되어 있다고 생각해보세요. 문이 무겁고, 힌지에서 문을 잡고 있습니다. 문이 움직이지 않을 때도 힌지는 문을 받쳐주는 힘을 계속 내고 있습니다(수직 방향 힘). 문을 살짝 놓으면 문이 무게 때문에 약간 돌아가게 됩니다. 이때 힌지는 여전히 문을 잡아주는 힘을 방향을 달리해서 계속 제공합니다. 문이 회전하는 순간에도 힌지는 수직 방향뿐 아니라, 문을 원하는 회전 궤도로 움직이게 하는데 필요한 수평 방향 힘(여기서는 회전하는 운동 방향에 해당하는 접선방향 힘)도 발생시킬 수 있습니다. 힌지가 없다면 문은 아래로 그냥 떨어지거나 제멋대로 움직이겠죠.
마찬가지로 이 원판 문제에서 O점은 원판이 임의의 방향으로 떨어지거나 움직이지 않고, 회전 운동을 하도록 길잡이 역할을 합니다. 이 역할을 하기 위해 O점은 접선방향으로 힘을 제공해야 합니다. 이 힘이 O_t입니다.
정리:
- O점(핀)이 움직이지 않는 것은 외부적으로 아주 단단히 고정되어 있다는 의미이지, 힘이 필요 없다는 뜻이 아닙니다.
- 원판이 회전 가속도를 가지려면 G점이 적절한 방향으로 가속해야 하고, 이를 위해 O점은 적절한 접선방향 힘을 원판에 가해줘야 합니다.
- 따라서 O점에서의 탄젠셜 반력 O_t는 0이 아니며, 이 값은 원판의 회전에 필요한 가속도(및 그에 따르는 운동방정식)를 통해 계산됩니다.
이렇게 생각하면 O점이 단순히 정지해 있지만, 그 정지는 반력이 0이라서가 아니라, 반대로 필요한 만큼의 반력을 통해 자신의 위치를 고정하고 원판의 운동을 제어하는 결과임을 알 수 있습니다.
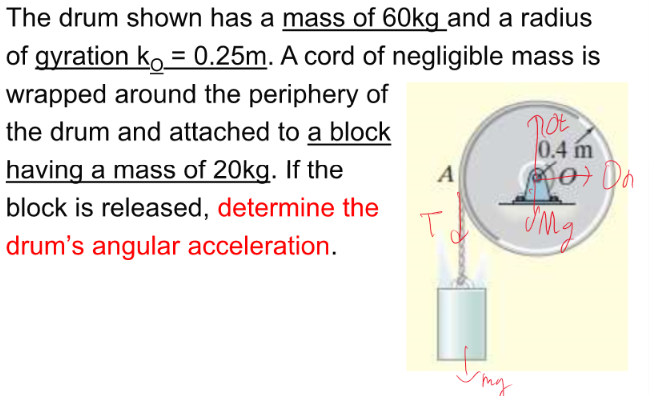
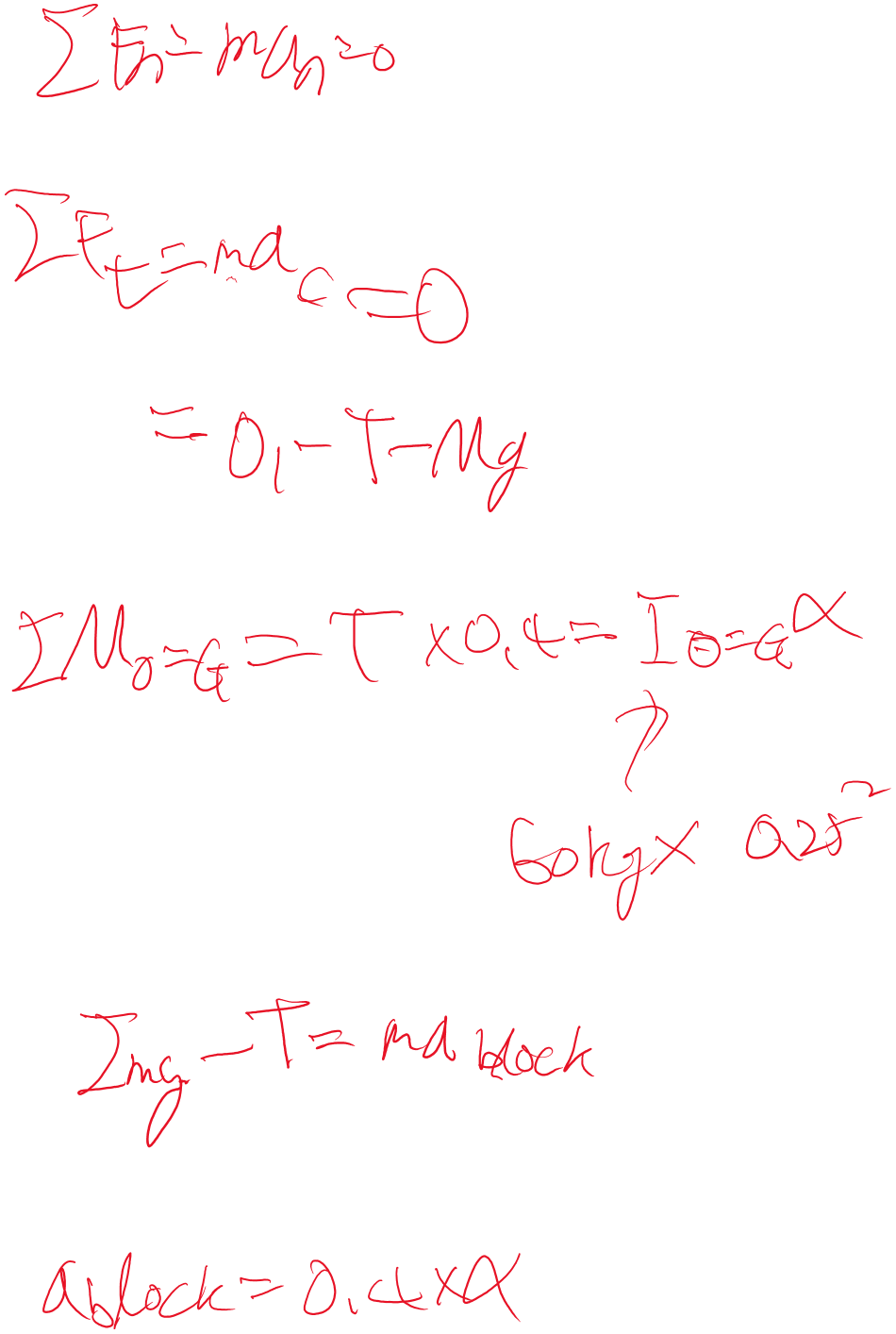
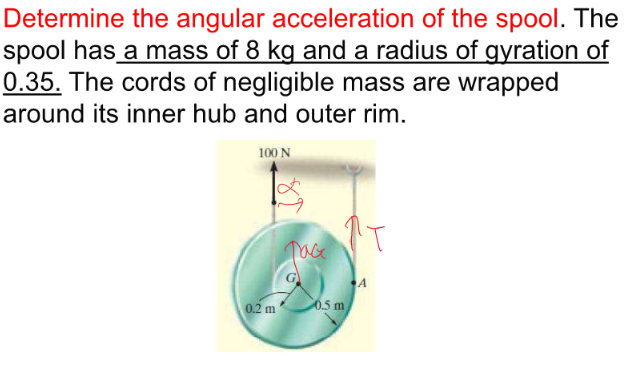
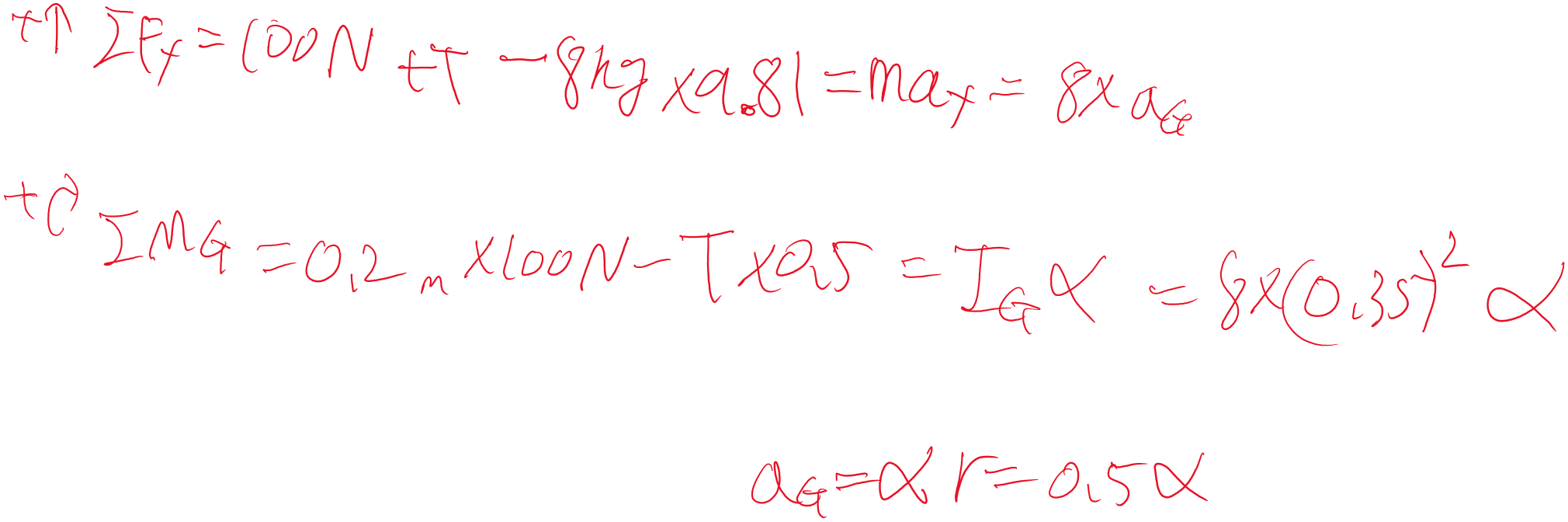
여기선 x방향 힘이 존재하지도 않기 때문에 없습니다.
존재하는 힘의 방향을 잘 나열하고, 모멘트도 잘 계산해서 작성하면 답이 뚝딱 나옵니다.
alpha * r = a만 잘 기억하면 다 풀수 있을 것 같네요

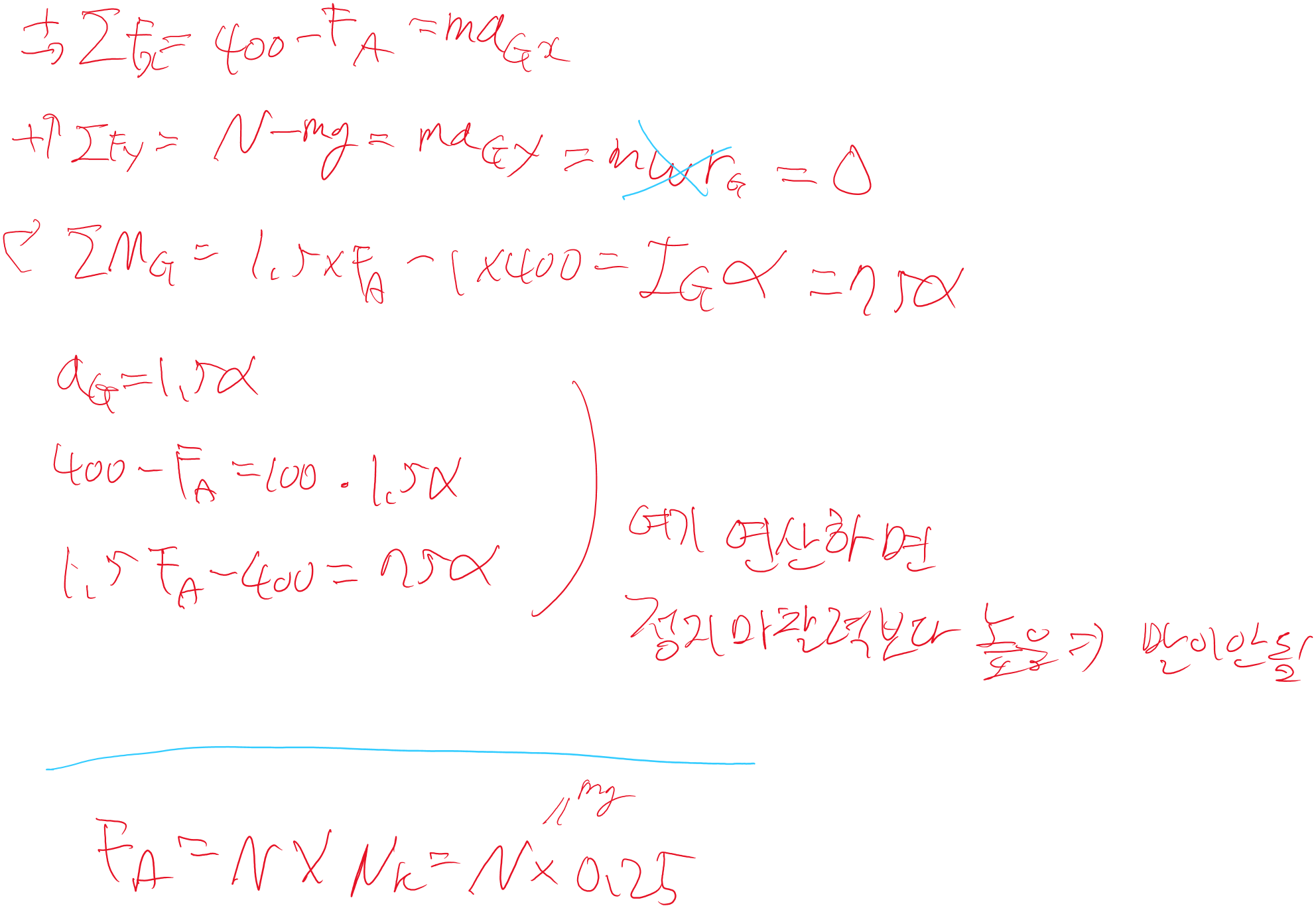
여기선 y방향 이동이 없으므로 합이 0이고, x와 모멘텀을 통해 값을 연산해서 정지인지, 이동인지 잘 구할수 있습니다.
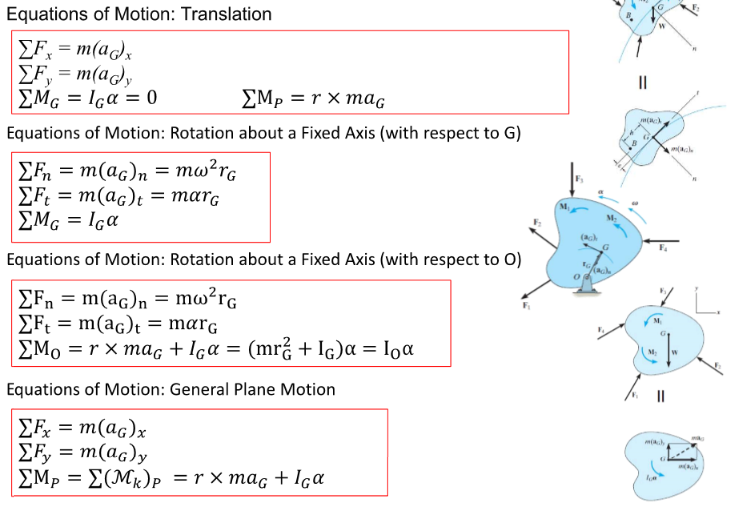
암기할 것이 자꾸 늘어나네요...
저는 물리랑 거리가 있긴 한가 봅니다...
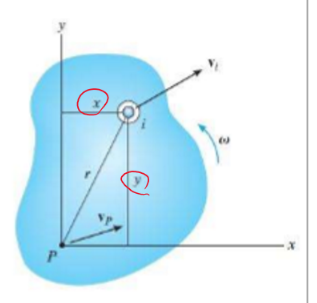
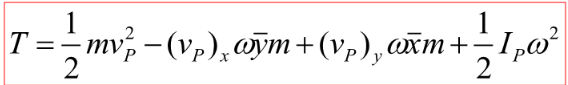
여기서 P를 어디에 두든 에너지는 동일하므로 질량 중심에 두어 연산이라도 편하게 하자!
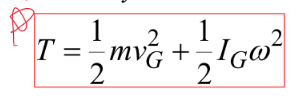
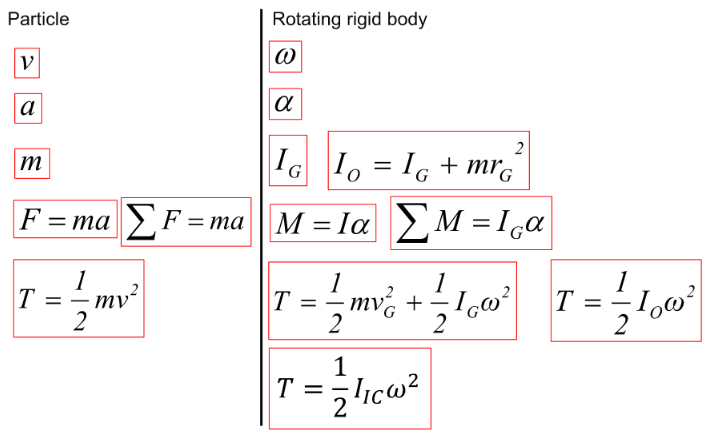


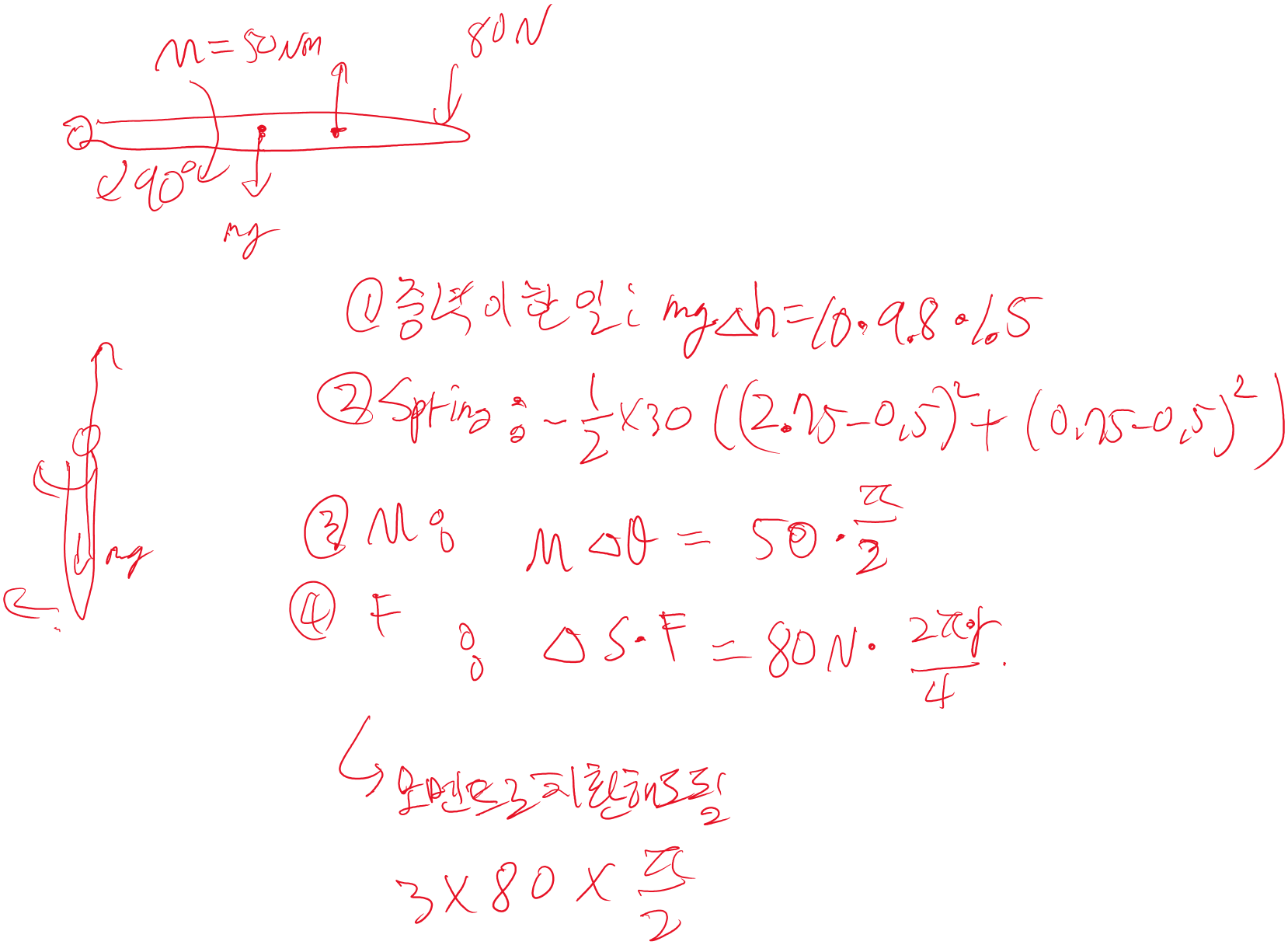
여기선 각각 무슨 힘이 들어가는지 다 확인 후에 이동거리를 곱하면 일이 뚝딱 나옵니다.

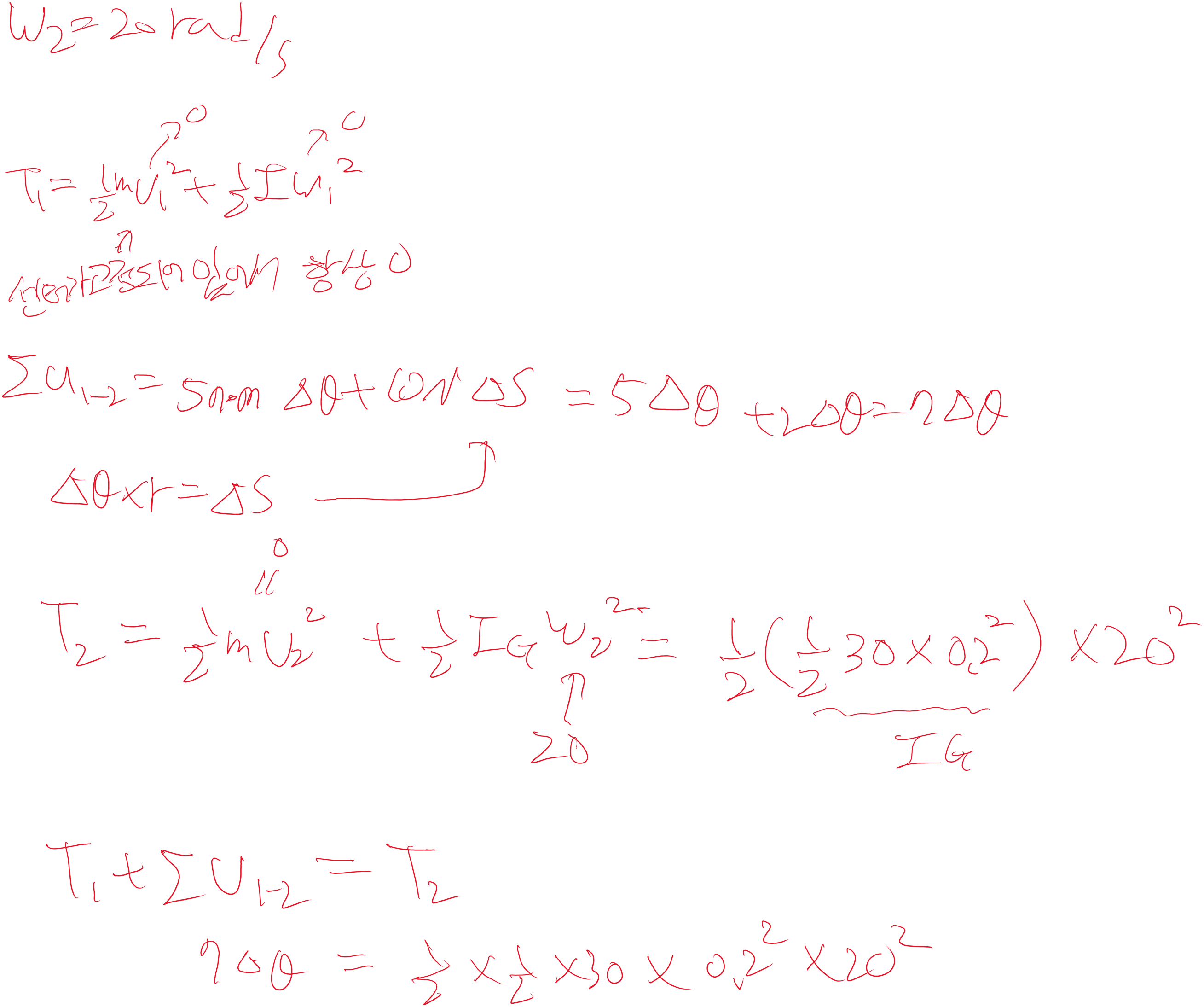

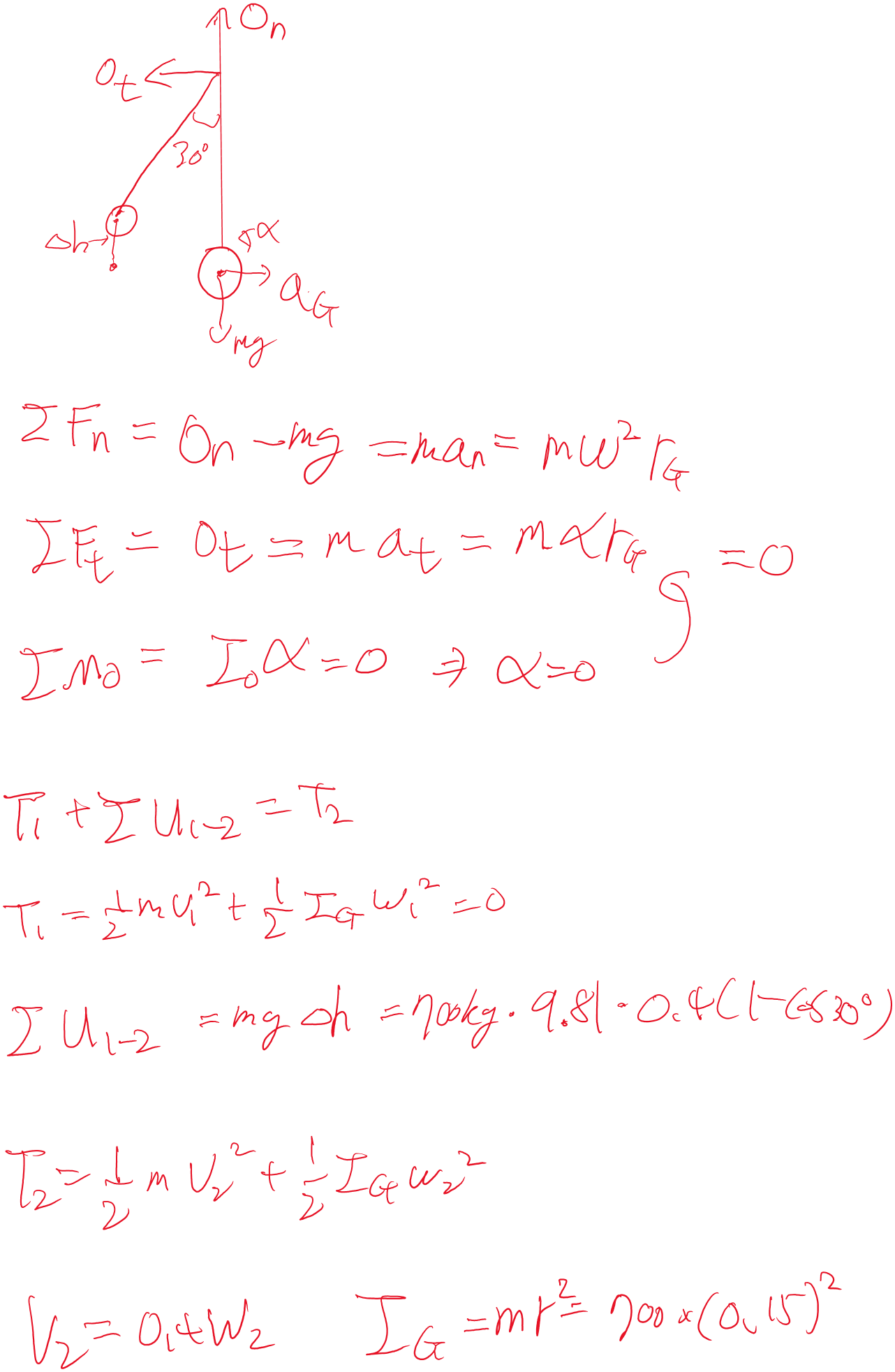
아래는 제시된 예제 상황(Example 18.4)을 물리를 처음 배우는 사람도 이해할 수 있도록 단계별로 쉽고 자세히 설명한 것입니다.
문제 상황 이해하기:
- 상황 개요:
700kg의 파이프가 지게차(forklift)의 두 개의 포크(갈퀴) 위에 균등하게 올려져 있다고 생각해보세요. 이 파이프는 줄로 매달려 있는 상태라 약간 흔들리는 '진자'처럼 움직일 수 있습니다. 문제에서는 파이프가 어떤 특정 순간에 각도 θ=30∘ 에서 잠시 멈추었다가, 중력에 이끌려 다시 θ=0∘ 즉 가장 아래 위치로 내려오는 상황을 다룹니다. - 질문:
θ=0∘위치, 즉 파이프가 맨 아래 위치에 있을 때, 두 개의 포크(타인, tine) 각각이 파이프를 지지하기 위해 필요로 하는 수직방향의 힘(노멀력)과 마찰력(수평방향 힘)을 구하라는 것입니다. - 왜 단순히 무게만 생각해서는 안 될까요? 파이프가 흔들려 내려오면 단순히 가만히 있는 경우보다 더 큰 힘이 필요할 수 있습니다. 왜냐하면 아래 위치로 떨어지는 동안 파이프가 속력을 갖게 되고, 그 상태에서 다시 위로 올라가지 않고 아래 지점에서 방향을 바꾸려면(즉, 원호운동을 계속하려면) 추가적인 "중심방향 가속도(원운동 시 필요한 가속도)"를 제공해야 하기 때문입니다. 이 가속도를 만들어주는 힘이 결국 포크가 파이프를 누르면서 생기는 노멀력에 반영됩니다.
물리 원리 정리하기:
- 에너지 변화:
파이프가 30° 위치에서 잠시 멈춰 있다면, 그때 파이프는 상대적으로 높은 위치에 있습니다. 그 후 0° 위치(가장 낮은 위치)로 내려오면서, 위치에너지가 운동에너지로 전환됩니다. 이로 인해 파이프는 0° 지점에서 어떤 속력을 가지게 됩니다. - 원운동(회전운동)에서의 힘 고려하기:
파이프는 매달린 점 O를 중심으로 흔들리는 진자처럼 생각할 수 있습니다. 파이프의 질량중심 G가 O를 중심으로 반지름 r(예: 문제 그림에서 0.4m 정도)이 있다고 할 때, 0° 지점에서 파이프는 속력을 가지며 원호 경로를 따라 움직이므로, 원운동에 필요한 ‘중심방향(중심가속도 방향)’의 힘이 필요합니다. 이 힘은 무엇으로부터 나올까요? 바로 파이프를 잡아주는 포크의 지지력(노멀력)입니다. 파이프는 포크 위에 놓여 있기 때문에, 포크가 위로 밀어 올리는 힘(노멀력)이 단순히 파이프의 무게를 지탱하는 것보다 커질 수 있습니다. 그 추가분은 파이프가 원운동을 하기 위한 '중심가속도'를 제공하기 위함입니다. - 마찰력의 역할:
파이프는 두 포크 위에 얹혀 있어 수평으로도 약간 움직일 수 있거나, 굴러가려는 경향이 있을 수 있습니다. 마찰력은 파이프가 좌우로 미끄러지지 않도록 잡아주는 힘입니다. 파이프가 흔들리며 운동을 하다 보면, 순간적으로 수평 방향으로 미끌림이 일어날 수 있는 상황이 생깁니다. 이 때 마찰력이 이를 방지해줍니다. - 즉, 노멀력은 '위로 지지하는 힘'이고, 마찰력은 '옆으로 미끄러지지 않도록 잡아주는 힘'입니다.
해결 과정 개략:
- 질량과 무게:
파이프 질량 m=700 kg
무게 W=mg=700×9.81≈6867 N - 30°에서 0°로 내려올 때의 속력 계산(개략):
30° 위에 있을 때의 위치에너지 감소분이 0°에서의 운동에너지로 전환됩니다. 이 과정을 통해 0°에서 파이프의 질량중심 G의 속도를 구할 수 있습니다. (문제에서 자세한 수치가 주어지면, 그걸로 계산 가능합니다.) 대략적으로 계산해보면 0°에서 약 1m/s 정도의 속도를 가지게 될 수 있습니다. - 0° 지점에서의 중심가속도(원운동 가속도):
원운동에서는 가속도=v2/r입니다. 속력이 생기면, 그 속력으로 곡선 경로(반경 r)를 유지하려면 v2r만큼의 중심가속도가 필요합니다. 이 가속도를 제공하기 위해서는 그 방향으로 추가적인 힘이 필요합니다. - 파이프의 무게는 아래 방향, 중심가속도를 위한 힘은 O점을 향하는 방향(0°에서는 O점이 바로 위쪽이므로, 중심가속도에 필요한 힘은 위로 작용)을 필요로 합니다. 즉, 결국 포크는 파이프를 더 강하게 위로 밀어줘야 합니다.
- 결과:
- 노멀력(N): 파이프 한 개를 지지하는 두 포크가 있으니, 총 필요 노멀력을 2로 나누면 각 포크에 걸리는 노멀력을 구할 수 있습니다. 이 노멀력은 단순히 무게를 반씩 나눈 것보다 큽니다. 왜냐하면 원운동을 위한 추가 힘을 제공해야 하기 때문입니다.
- 마찰력(F): 마찰력은 파이프가 옆으로 미끄러지려는 경향을 억제합니다. 0° 위치에서 파이프가 수평방향으로 속력을 가지면, 잠깐이라도 수평 방향으로 힘의 균형이 필요하게 됩니다. 마찰력은 이 때 필요한 수평 힘을 제공하여 파이프가 자리 이탈을 방지합니다.
- 수직방향 노멀력: 파이프 무게를 지탱하는 것보다 더 큰 값 (무게 + 추가 중심가속도에 해당하는 힘)
- 수평방향 마찰력: 파이프가 옆으로 미끄러지지 않게 잡아주는 힘
쉽게 비유하기:
진자처럼 줄에 매달린 공을 생각해봅시다. 공을 한쪽으로 들어올려놓았다가(30°) 놔주면 (0°) 가장 낮은 점을 지날 때 공은 가장 빠른 속력을 가지게 됩니다. 이때 줄이 공을 잡아당기는 힘은 단순히 공의 무게보다 커져야 합니다. 왜냐하면 공이 직선이 아닌 곡선 경로를 따라 움직이려면 "추가적인 당기는 힘"이 필요하기 때문입니다. 그 힘이 바로 줄의 장력으로 나타나며, 여기서는 그 역할을 포크의 노멀력이 하는 것입니다. 마찰력은, 만약 공이 좌우로 미끄러지려 한다면 줄 또는 지지점이 이를 막아주는 것처럼, 파이프가 포크 위에서 쉽게 굴러가지 않도록 잡아주는 역할을 합니다.
이런 식으로 파이프가 0° 지점에서 필요로 하는 노멀력과 마찰력을 구하게 되면, 단순 정적 하중보다 큰 수직력과 일정한 수평 마찰력이 필요함을 알 수 있습니다. 이 힘들을 통해 지게차 포크는 파이프가 흔들리면서도 제자리를 유지하도록 하는 것이죠.
'기타' 카테고리의 다른 글
| 협상 프로세스에 관한 연구 : 협상전술, 정보교환, 그리고 협상성과간의 관계 - 논문 리뷰 (1) | 2024.12.10 |
|---|---|
| 동역학 14주차 (0) | 2024.12.08 |
| 동역학 12주차 정리 (0) | 2024.12.07 |
| AI for Global Climate Cooperation: Modeling Global Climate Negotiations, Agreements, and Long-Term Cooperation in RICE-N - 논문리 (2) | 2024.12.05 |
| 역사와 한국의 영토 12주차 - 한 일 관계 (0) | 2024.12.02 |