시험 전 마지막 진도가 충돌이었습니다.

그래서 나왔던 식은 위와 같았습니다.
이제부턴 충돌에 각이 생기고, Line of impact만 생각해서 연산하면 됩니다.


이 문제에서 사이즈는 무시해도 됩니다.
X축 충돌만 존재하므로 y축 속도는 변함 없고, mv + mv = mv + mv에 잘 넣어서 연산하고, e = (v - v) / (v - v)를 구하면 끝 입니다.
이제 각 운동량이 나옵니다.
운동량은 물체의 운동 상태를 나타내는 물리량으로, 크게 두 가지 종류가 있습니다: 선운동량(Linear Momentum)과 각운동량(Angular Momentum). 각각에 대해 자세히 설명하면 다음과 같습니다:
1. 선운동량 (Linear Momentum)
정의
- 선운동량은 질량이 있는 물체가 일정한 속도로 운동할 때, 그 운동 상태를 나타내는 물리량입니다.
- 물리적으로는 물체의 질량과 속도의 곱으로 정의됩니다.
수식
p=mv
- p: 선운동량 (벡터)
- m: 물체의 질량 (스칼라)
- v: 물체의 속도 (벡터)
특징
- 보존 법칙: 외부 힘이 작용하지 않는 계에서 선운동량은 보존됩니다.
- 예: 충돌 및 폭발 현상에서 선운동량 보존 법칙이 적용됨.
- 선운동량은 힘과 밀접한 관계가 있으며, 뉴턴의 운동 제2법칙(F=ma)을 운동량으로 표현하면 다음과 같습니다: F=dp/dt
여기서 힘은 운동량의 시간 변화율임을 알 수 있습니다.
2. 각운동량 (Angular Momentum)
정의
- 각운동량은 물체가 회전하거나 원운동을 할 때 그 운동 상태를 나타내는 물리량입니다.
- 물리적으로는 물체의 위치 벡터와 선운동량 벡터의 외적(크로스 곱)으로 정의됩니다.
수식
L=r×p
또는
L=Iω
- L: 각운동량 (벡터)
- r: 위치 벡터 (물체와 회전축 사이의 거리)
- p: 선운동량
- I: 관성모멘트 (회전축에 대한 질량 분포)
- ω: 각속도 (rad/s)
특징
- 보존 법칙: 외부로부터의 순수한 토크(돌림힘)가 없는 경우, 각운동량은 보존됩니다.
- 예: 피겨스케이터가 회전 중 팔을 오므릴 때 회전 속도가 증가함.
- 각운동량은 토크와 밀접한 관계가 있으며, 토크는 각운동량의 시간 변화율로 표현됩니다:
τ=dL/dt
여기서 τ는 토크를 나타냅니다.
선운동량과 각운동량의 차이
특징선운동량각운동량| 운동 유형 | 직선 운동 | 회전 운동 |
| 정의 | p=mv | L=r×p 또는 L=Iω |
| 보존 법칙 | 외부 힘이 없을 때 보존됨 | 외부 토크가 없을 때 보존됨 |
| 단위 | kg·m/s | kg·m^2/ |
응용 예시
- 선운동량: 자동차 충돌 사고 분석, 로켓 발사 설계, 공의 운동.
- 각운동량: 자이로스코프 안정화, 인공위성 궤도 조정, 피겨스케이터 회전 동작.
위의 내용을 바탕으로 각 운동량의 정의와 특징을 이해하고, 관련 문제를 해결할 때 활용할 수 있습니다! 추가로 궁금한 점이 있으면 알려주세요. 😊
외적(Cross Product)은 벡터 대 벡터의 연산으로, 두 벡터가 만드는 평면에 수직한 새로운 벡터를 생성합니다. 주로 3차원 공간에서 정의되며, 물리학과 공학에서 널리 사용됩니다. 외적은 두 벡터 간의 면적, 회전 방향, 그리고 힘과 운동의 관계를 설명할 때 중요합니다.
외적의 정의
두 벡터 와 의 외적은 다음과 같이 정의됩니다:
A×B=∣A∣∣B∣sinθ n^
- A,B: 두 벡터
- ∣A∣,∣B∣: 벡터의 크기
- θ: 두 벡터 사이의 각도 (0∘≤θ≤180∘)
- n^: 두 벡터가 이루는 평면에 수직인 단위 벡터. 오른손 법칙에 의해 방향이 결정됩니다.
외적의 계산
외적은 성분 형태로 다음과 같이 계산됩니다. 두 벡터 A=(Ax,Ay,Az)와 B=(Bx,By,Bz)가 주어질 때:

여기서 i^,j^,k^는 각각 x,y,z축의 단위 벡터입니다.
결과는 다음과 같은 벡터입니다:
A×B=(AyBz−AzBy)i^−(AxBz−AzBx)j^+(AxBy−AyBx)k^
외적의 성질
- 크기: 외적의 크기는 두 벡터가 이루는 평행사변형의 면적입니다.
∣A×B∣=∣A∣∣B∣sinθ|- θ=90∘일 때, ∣A×B∣=∣A∣∣B∣.
- θ=0∘ 또는 180∘일 때, ∣A×B∣=0 (두 벡터가 평행함).
- 방향: 외적 벡터의 방향은 오른손 법칙에 따라 결정됩니다.
- A를 B 방향으로 회전시킬 때, 오른손의 엄지손가락이 가리키는 방향이 외적 벡터의 방향입니다.
- 비교:
- 교환 법칙: A×B=−(B×A)
- 분배 법칙: A×(B+C)=A×B+A×C
- 평행 관계: 두 벡터가 평행(또는 반평행)하면 A×B=0.
외적의 응용
- 물리학에서의 사용
- 토크: 힘과 거리 벡터의 외적으로 정의됨.
τ=r×F
여기서 r은 회전축에서의 위치 벡터, F는 작용하는 힘. - 각운동량: 위치 벡터와 선운동량의 외적으로 계산.
L=r×p
- 토크: 힘과 거리 벡터의 외적으로 정의됨.
- 기하학
- 두 벡터로 이루어진 평면의 면적 계산.
- 벡터의 수직성과 평행성 판단.
- 컴퓨터 그래픽스
- 법선 벡터 계산: 폴리곤의 표면 방향 계산.
외적의 직관적 이해
외적은 다음과 같은 물리적 상황에서 직관적으로 이해할 수 있습니다:
- 두 벡터의 평면을 손으로 잡고, 그 평면에 수직한 벡터를 상상해보세요.
- 오른손 법칙으로 방향을 파악하고, 두 벡터 사이의 교차적인 힘 또는 회전 효과를 시각화하면 더 쉽게 이해할 수 있습니다.
추가로 궁금한 점이 있으면 알려주세요! 😊
운동량, 충돌, 에너지, 힘은 물리학에서 운동과 상호작용을 이해하는 핵심 개념들입니다. 각각의 정의와 특성을 비교하면서 설명하면 다음과 같습니다:
1. 운동량 (Momentum)
- 정의: 운동량은 물체의 운동 상태를 나타내는 물리량으로, 물체의 질량과 속도의 곱으로 정의됩니다.
p=mv - 특징:
- 벡터량: 크기와 방향을 가짐.
- 보존 법칙: 외부 힘이 없으면 운동량은 보존됨(충돌에서 주로 사용).
- 역할:
- 충돌 및 폭발 현상에서 중요한 물리량.
- 힘과 시간의 관계를 나타냄:
Δp=F⋅Δt
2. 충돌 (Collision)
- 정의: 두 물체가 상호작용하여 운동 상태를 변화시키는 물리적 사건.
- 특징:
- 운동량 보존: 충돌 동안 전체 운동량은 항상 보존됨.
- 에너지 변화: 충돌의 종류에 따라 에너지가 보존되거나 일부 손실됨.
- 탄성 충돌: 운동 에너지와 운동량 모두 보존.
- 비탄성 충돌: 운동량은 보존되지만 운동 에너지는 일부 손실됨.
- 수식:
- 탄성 충돌: m1v1+m2v2=m1v1′+m2v2′ (속도와 운동량 보존식을 결합하여 계산)
3. 에너지 (Energy)
- 정의: 일을 할 수 있는 능력으로, 운동 에너지와 위치 에너지로 구분됨.
- 종류:
- 운동 에너지: 물체의 운동과 관련된 에너지. KE=1/2 mv^2
- 위치 에너지: 위치에 의해 저장된 에너지 (예: 중력 위치 에너지 PE=mgh).
- 보존 법칙:
- 보존력이 작용하는 경우, 전체 에너지(운동 에너지 + 위치 에너지)는 보존됨.
- 충돌 시, 탄성 충돌에서는 운동 에너지가 보존되지만, 비탄성 충돌에서는 일부가 열, 소리 등 다른 형태로 변환됨.
- 역할:
- 물체의 상태 변화(속도 변화 등)와 관련.
4. 힘 (Force)
- 정의: 물체의 운동 상태(속도)를 변화시키는 상호작용. F=ma
- 특징:
- 벡터량: 크기와 방향을 가짐.
- 물체에 작용하는 순간적인 영향으로 운동량의 변화율을 나타냄: F=dp/dt
- 역할:
- 물체를 가속시키거나 정지시키는 데 필요.
- 운동량과 에너지를 변화시키는 원인.
비교 및 상호작용
| 운동량 | 질량과 속도의 곱 (p=mv) | 외부 힘이 없을 때 보존 | 충돌에서 운동량 보존 법칙을 통해 두 물체의 최종 속도를 계산. |
| 충돌 | 두 물체의 상호작용 | 운동량 보존. 에너지는 탄성 여부에 따라 다름. | 충돌 시 운동량과 에너지 보존 법칙을 동시에 활용. |
| 에너지 | 일을 할 수 있는 능력 (KE,PE) | 보존력 하에서 보존 | 운동량의 크기와 운동 에너지 간에는 KE=p^2/2m관계 성립. |
| 힘 | 가속도를 유발하는 요인 (F=ma) | 일반적으로 보존되지 않음 | 힘이 시간에 걸쳐 작용하면 운동량 변화 (Δp)를 유발. |
직관적 이해
- 운동량 vs. 에너지:
- 운동량은 물체의 운동 상태(방향과 크기 모두)를 나타냄.
- 운동 에너지는 운동의 "총량"을 나타냄(방향이 없음).
- 예: 대형 트럭과 소형 자동차가 같은 속도로 움직일 때, 대형 트럭은 더 큰 운동량과 운동 에너지를 가짐.
- 충돌에서 운동량과 에너지의 역할:
- 충돌 동안 운동량은 항상 보존되지만, 에너지는 충돌의 성격에 따라 다르게 변화.
- 탄성 충돌에서는 운동량과 운동 에너지가 모두 보존.
- 비탄성 충돌에서는 운동 에너지 일부가 열, 소리 등으로 전환.
- 힘과 운동량:
- 힘은 운동량을 변화시키는 원인.
- 예: 야구공을 치는 방망이는 순간적인 큰 힘을 가하여 공의 운동량과 속도를 급격히 변화시킴.
이렇게 네 가지 개념은 각각의 특성과 보존 법칙을 기반으로 상호작용하며, 물체의 운동과 변화를 설명하는 데 긴밀히 연결됩니다. 😊
개념정의보존 여부수식응용 사례
| 개념 | 정의 | 보존 여부 | 수식 | 응용사례 |
| 운동량 (Momentum) |
물체의 질량과 속도의 곱. | 외부 힘이 없으면 보존 | p=mv | 충돌 분석, 로켓 운동, 자동차 안전 설계 |
| 각운동량 (Angular Momentum) |
회전 운동 상태를 나타내는 물리량. 질량 분포와 각속도의 곱으로 나타냄. | 외부 토크가 없으면 보존 | 자이로스코프 안정화, 위성 자세 제어, 회전 운동 해석 | |
| 에너지 (Energy) |
일을 할 수 있는 능력. 운동 에너지와 위치 에너지로 구분. | 보존력 작용 시 보존 | KE=1/2 mv^2, PE=mgh |
발전소 설계, 충돌 에너지 분석, 기계 시스템 효율 평가 |
| 힘 (Force) |
물체의 운동 상태(속도)를 변화시키는 원인. | 일반적으로 보존되지 않음 | , F=dp/dt |
자동차 가속, 건물 구조 설계, 발사체 추진력 계산 |
| 토크 (Torque) |
회전 운동을 유발하는 힘의 효과. | 외부 토크가 없으면 각운동량 보존 | , τ=I * dω/dt |
회전 축 설계, 공학 기계 분석, 드릴 작동 원리 |
| 일 (Work) |
힘이 물체에 가해져서 물체를 이동시킬 때 전달된 에너지. | 보존력에 의해 발생하는 경우 위치 에너지로 전환 | , W=∫F⋅ds |
기계적 에너지 전달, 도르래 및 지렛대 효율 분석 |
| 파워 (Power) |
단위 시간당 전달된 에너지. | 일반적으로 보존되지 않음 | , P=F⋅v |
전력 생산, 기계 효율 평가, 에너지 소비 계산 |
| 충격량 (Impulse) |
운동량의 순간적 변화량. | 외부 힘이 일정 시간 동안 작용한 결과로 표현 | J=Δp, J=F⋅Δt |
야구공 타격, 충돌 방지 설계, 자동차 에어백 설계 |
| 압력 (Pressure) |
단위 면적당 작용하는 힘. | 보존되지 않음 | P=F/A | 수압 계산, 항공기 설계, 다이빙 기어 설계 |
| 탄성력 (Elastic Force) |
변형된 물체가 원래 상태로 돌아가려는 복원력. | 훅의 법칙 범위 내에서 보존 | F=−kx | 스프링 설계, 진동 분석, 구조물 내 응력 해석 |
| 마찰력 (Friction) |
두 표면 간 상대 운동을 방해하는 힘. | 일반적으로 에너지 소모로 이어짐 | F_f=μF_n | 자동차 타이어 설계, 기계 효율 분석, 표면 마찰 해석 |
| 중력 (Gravity) | 질량을 가진 물체들 사이의 인력. | 중력장에서 위치 에너지는 보존됨 | , PE=mgh |
행성 궤도 계산, 건축 구조 해석, 우주 탐사 |
벡터의 단위벡터 를 곱했을 때 결과는 외적(Cross Product) 규칙에 따라 결정됩니다. 이를 이해하려면 오른손 법칙과 부호를 결정하는 순환 규칙을 기억하면 됩니다.
1. 기본 단위벡터
- : x-축 방향 단위벡터
- : y-축 방향 단위벡터
- : -축 방향 단위벡터
2. 단위벡터 간 외적의 결과
(1) 자기 자신과의 외적
- 단위벡터와 자기 자신을 외적하면, sin(0∘)=0이므로 결과는 0입니다.
i×i=j×j=k×k=0
(2) 다른 단위벡터 간 외적
- 오른손 법칙과 순환 규칙에 따라 결과가 결정됩니다.
- 순환 규칙:
i×j=k, j×k=i, k×i=j(벡터 순서가 순환적이면 양의 부호를 가집니다.) - 반대 순서일 경우, 결과는 음수가 됩니다.j×i=−k, k×j=−i, i×k=−j
3. 정리된 표
외적결과| i×i | 0 |
| 0 | |
| 0 | |
| k | |
| i | |
| j | |
| −k | |
| −i | |
| −j |
4. 오른손 법칙으로 기억하기
- 첫 번째 벡터 A를 손바닥으로 향하게 하고, 손가락을 두 번째 벡터 B 방향으로 구부립니다.
- 엄지손가락이 A×B의 방향을 가리킵니다.
5. 쉽게 부호를 기억하는 팁
- 순환적 순서 (i→j→k→i)이면 결과는 양수.
- 역순 (i→k→j→i)이면 결과는 음수.
이 표와 규칙을 기억하면 단위벡터 간의 외적 결과를 헷갈리지 않게 사용할 수 있을 거예요! 😊
자세가 변하면 각 속도가 변하고, 외부와 충돌이 없으니 보존이 된다. -> 넓게 있을 땐 천천히 돌고, 좁게 있을 땐 빠르게 돈다.
일 - 같은 힘에서 두 배의 거리를 갔다면 두 배의 일을 한 것임


기존 운동량 + 충격량 = 나중 운동량
dr/dt * mv = v * mv = 0
=> H'O = r' +\*mv + r * mv' = r * mv'
각 충격량, 각 운동량, 그리고 각 운동량 보존은 회전 운동에서 중요한 개념입니다. 각각의 정의와 수식, 특징, 그리고 상호 관계를 상세히 설명하겠습니다.
1. 각 충격량 (Angular Impulse)
정의
각 충격량은 물체에 가해진 토크(돌림힘)가 시간 동안 작용하여 물체의 각운동량을 변화시키는 물리량입니다.
선형 운동에서 충격량이 운동량을 변화시키듯, 각 충격량은 각운동량을 변화시킵니다.
수식
각 충격량 Jτ는 토크 τ와 작용 시간 Δ의 곱으로 정의됩니다.
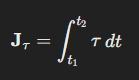
특징
- 단위: N·m·s (뉴턴 미터 초).
- 각운동량 변화와의 관계:
- 각 충격량은 각운동량의 변화와 같음:
Jτ=ΔL=Lf−Li 여기서 Li는 초기 각운동량, Lf는 최종 각운동량.
- 각 충격량은 각운동량의 변화와 같음:
2. 각 운동량 (Angular Momentum)
정의
각 운동량은 물체가 회전할 때 운동 상태를 나타내는 물리량으로, 물체의 질량 분포와 각속도의 곱으로 정의됩니다. 이는 회전 운동의 관성을 나타냅니다.
수식
- 점 질량에 대한 정의:L=r×p
- r: 물체의 위치 벡터.
- p=mv: 선운동량.
- L: 각운동량.
- 회전 운동체에 대한 정의:L=Iω
- I: 관성모멘트(물체의 질량 분포와 회전축에 대한 거리의 제곱 합).
- ω: 각속도 벡터.
특징
- 단위: kg·m^/s
- 벡터량: 크기와 방향을 가짐.
- 방향은 회전축을 따라 오른손 법칙으로 결정됨.
- 보존: 외부 토크가 없는 경우 각운동량은 보존됨.
3. 각 운동량 보존 (Conservation of Angular Momentum)
정의
외부로부터의 순수한 토크(돌림힘)가 작용하지 않는다면, 계의 총 각운동량은 시간에 따라 변하지 않고 일정하게 유지됩니다.
수식

- τexternal=0=이면, L=는 일정:
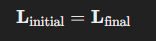
특징
- 보존 조건: 외부 토크가 없거나, 내부 힘들만 작용할 때.
- 적용 예시:
- 피겨스케이터가 팔을 오므릴 때:
- 가 감소하면 ω가 증가(회전 속도 증가).
- 지구와 태양의 상호작용:
- 지구의 궤도 각운동량은 외부 토크가 거의 없기 때문에 보존됨.
- 피겨스케이터가 팔을 오므릴 때:
실제 의미
- 각운동량 보존 법칙은 회전 운동의 상태를 예측하고 이해하는 데 중요.
- 외부 영향을 줄이면 회전체의 각속도 또는 질량 분포를 조작하여 회전을 제어 가능.
4. 각 충격량, 각 운동량, 각 운동량 보존 간의 관계
이들 간의 관계는 선운동에서의 충격량, 운동량, 운동량 보존과 유사합니다.
| 각 충격량 | 토크와 작용 시간의 곱 | Jτ=∫τdt | 각운동량 변화를 유발. |
| 각 운동량 | 회전 운동의 운동량 | L=Iω | 외부 토크가 없으면 보존. |
| 각 운동량 보존 | 외부 토크가 없는 경우 각운동량은 일정 | Linitial=Lfinal | 회전 운동이 유지되는 조건. |
응용 예시
- 스포츠:
- 피겨스케이팅 회전 동작에서 팔을 펼치거나 오므리면서 회전 속도를 조절.
- 다이빙에서 몸을 구부려 회전 속도를 증가.
- 천체 물리학:
- 별이 수축하여 블랙홀이 될 때, 각운동량 보존에 의해 회전 속도가 급격히 증가.
- 기계 공학:
- 자이로스코프를 이용한 안정화 기구.
- 드론의 회전 안정성 제어.
- 일상 생활:
- 의자에 앉아 회전하며 팔을 펼치거나 오므려 회전 속도를 느껴보기.
요약
- 각 충격량은 외부 토크가 작용하여 각운동량을 변화시키는 원인.
- 각 운동량은 물체의 회전 운동 상태를 나타내는 기본적인 물리량.
- 각 운동량 보존은 외부 토크가 없을 때 회전 운동의 상태를 설명하는 강력한 법칙으로, 다양한 물리 현상을 예측하고 설명하는 데 사용됩니다. 😊
각 운동량은 보존된다
H0 = r * mv => r이 작아지면 v가 빨라진다.


Ho1은 구형 구조물에 항상 수직으로 가해지므로 r x mv = rmv이나 v=0이므로 rmv = 0이다.
Ho2 = 2rmv_2
해서 구하면 된다.

M = H'
=> r x F = r x mv'
=> r x mg = r mg sin theta = mv'

m, r1, v1이 나와있다. r2가 나와있으니 v2는 금방 구한다.
m * r1 * v1 = m * v2 * v2' 이므로 v2' = 3이다. vc = 2 이므로 이 것을 통해 v2를 구한다.
이제 0.5 m * v^2 + U = 0.5 m * v^2을 통해 U를 구하면 끝이다.
Chapter 16: Planar Kinematics of a Rigid Body
강체의 평면 운동학
1. Translation - 병진, 직선, 곡선
움직임이 같고 평행하다.

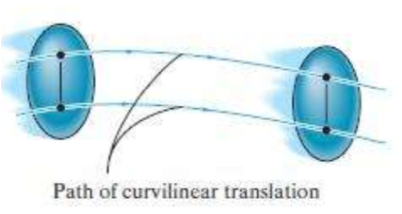
2. Rotation about a fixed axis - 고정축 중심의 회전 운동

3. General plane motion - 일반 평면 운동
회전축이 이동한다.
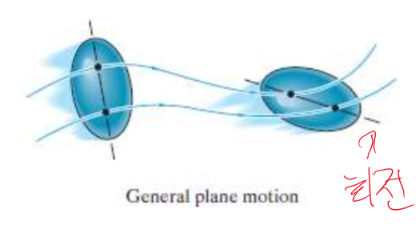

r_B = r_A + r_(B/A)


각 가속도도 기존 가속도와 동일하게 진행된다.
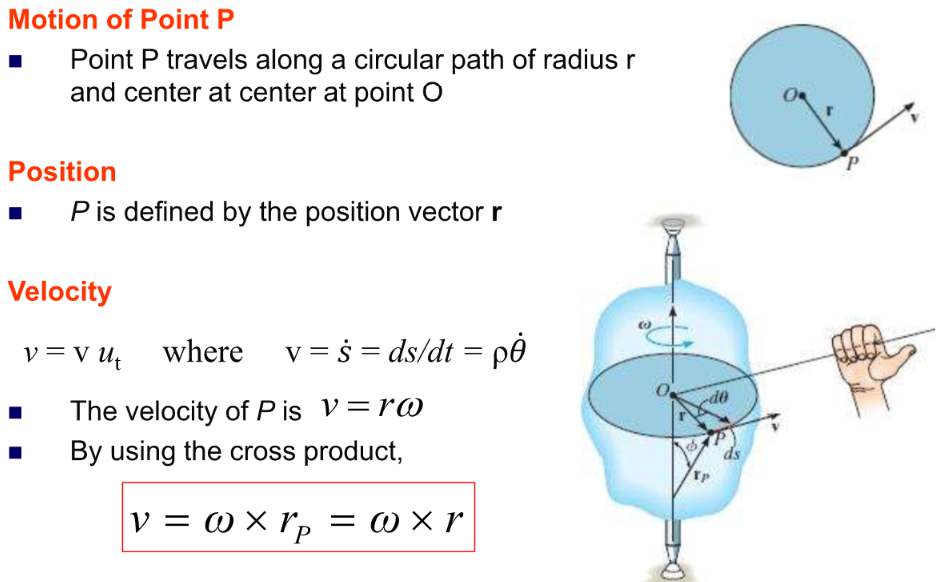

w = dθ / dt
a = dw / dt
a dθ = w dw


반지름 비율에 따라 가속도를 구할 수 있다.
구한 가속도를 적분하여 속도, 위치를 구할 수 있다.

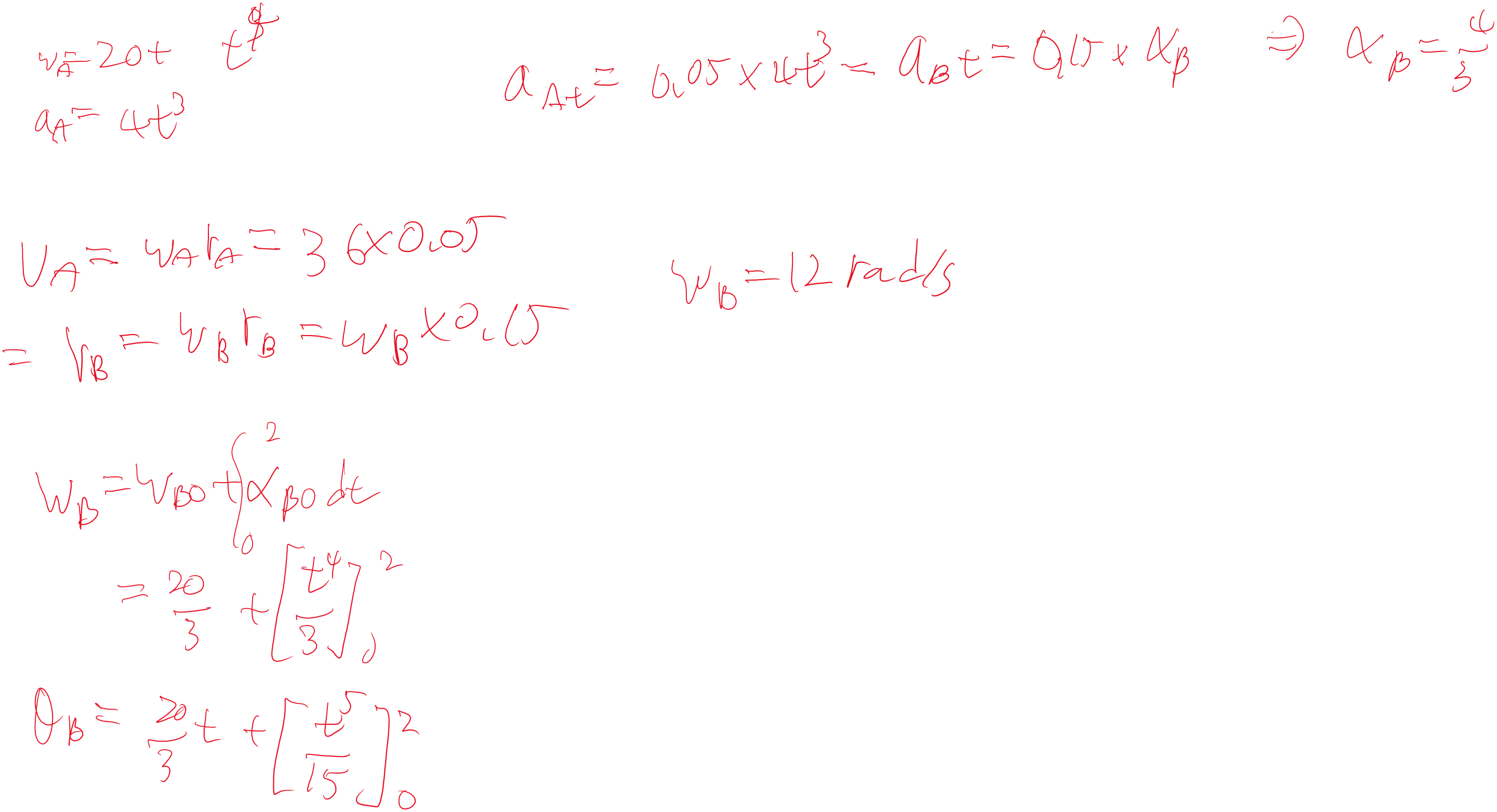
여기서도 시간에 대한 각 가속도를 줬다. 이를 통해서 각 속도를 구하고, 반지름에 따른 각 가속도를 구할 수 있다.
나머지는 적분을 통해 구할 수 있다.


여기도 풀이 방식은 비슷하다.
'기타' 카테고리의 다른 글
| 동역학 11주차 정리 (0) | 2024.11.18 |
|---|---|
| 동역학 10주차 정리 (1) | 2024.11.18 |
| 학술제 준비 겸 자료 저장용 (0) | 2024.11.15 |
| 역사와 한국의 영토 10주차 - 독도 영유권 (2) | 2024.11.06 |
| 역사와 한국의 영토 9주차 - 해방 이후의 독도 (1) | 2024.11.06 |