
속력이 시간에 대한 함수로 주어지고, 위치와 가속력을 t=3 일 때 구하라고 한다.
이건 그냥 미분과 적분하면 끝!

초기 속도, 초기 위치가 주어졌다.
위로 가는 것이니 가속도도 주어진 셈이고 이다.
v=0일 때 t 를 구해서 적분하여 s를 구할 수 있고, 여기서 s= 0일 때 t를 구하여 다시 v를 구할 수 있다.
여기에 나온 vdv = ads를 사용하진 않을 것 같다.
계산이 편할 것 같긴 하지만 시험 땐 내가 편한 방식으로 풀 것 같아서...

초기 속도, 위치, 가속도가 s에 관한 식으로 주어졌다.
v와 t를 구하는 문제다
이 문제는 v dv = a ds를 통해서 v를 먼저 구한다. 그리하여 s일 때 속도를 구할 수 있다.
그 다음 v = ds/dt => v dt = ds 를 통해 t에 관한 식을 뽑아 낼 수 있다.
그리하여 t를 구하면 된다.

너무 다 잊어먹었다...

v를 t에 관한 시간으로 줬으니 적분하면 s를 구할 수 있습니다.
t=2일 때 바뀌는 것 같으니 속도를 구할 땐 그냥 적분하고, 속력을 구할 땐 두번에 나눠서 구해서 더하면 됩니다.

v-t 그래프는 s 그래프 그대로 미분해서 그리고, a-t 그래프는 그 v-t 그래프를 미분해서 그리면 끝 입니다.

v-t 그래프는 t=10을 기준으로 좌우 적분해서 각각 그리고, s-t 그래프도 그대로 t=10 기준으로 좌우 나눠서 그리면 됩니다.
연속 되게 그려야 합니다!

x가 t에 관한 식으로 나왔으니 x 미분해서 먼저 x방향 속도랑 가속도 구해줍니다.
그리고 y를 미분하여 위에서 구한 x를 대입하면 y에 대한 속도랑 가속도도 구할 수 있습니다.
이 두개를 사용해서 각각 제곱해서 더하고 루트 씌어서 속력, 가속력 구할 수 있고, arctan 통해서 각도도 구할 수 있습니다

여기선 y가 x에 대한 식으로 나오고, y의 속도, y의 위치가 나와 있습니다.
그럼 y의 가속도는 0이고, 이 것을 통해 y를 미분해가면서 x의 위치, 속도, 가속도를 다 구할 수 있습니다.
그럼 다 구할 수 있습니다.

va가 나와있으니 이 것을 통해서 x, y 방향 속도를 구할 수 있습니다.
그럼 y방향 속도에 중력 가속도를 포함하여 적분하고, -150일 때의 시간을 구할 수 있습니다.
그럼 x 방향 속도를 적분해서 R을 구할 수 있습니다.

v0를 통해 vx, vy를 모두 구할 수 있습니다. 거기서 x는 6미터로 정해졌으므로 t를 구할 수 있고, 그 것을 통해 y를 구해 h를 구할 수 있습니다.

각도가 나왔으니 va를 각각 vx, vy로 나눌 수 있습니니다.
미지수로 va는 계속 두고, x = 80, y = 64를 통해서 va, t에 관련된 식 2개가 남으니 구할 수 있습니다.

v가 s에 관한 식으로 주어졌고, s = 10일 때의 가속력을 구하면 됩니다.
an은 반지름과 v가 있으니 구할 수 있지만 at는 v를 t 로 미분해야 해서 애매해졌습니다.
v' = dv / dt = dv / ds * ds / dt = 2 * v = 4s 해서 구할 수 있습니다.
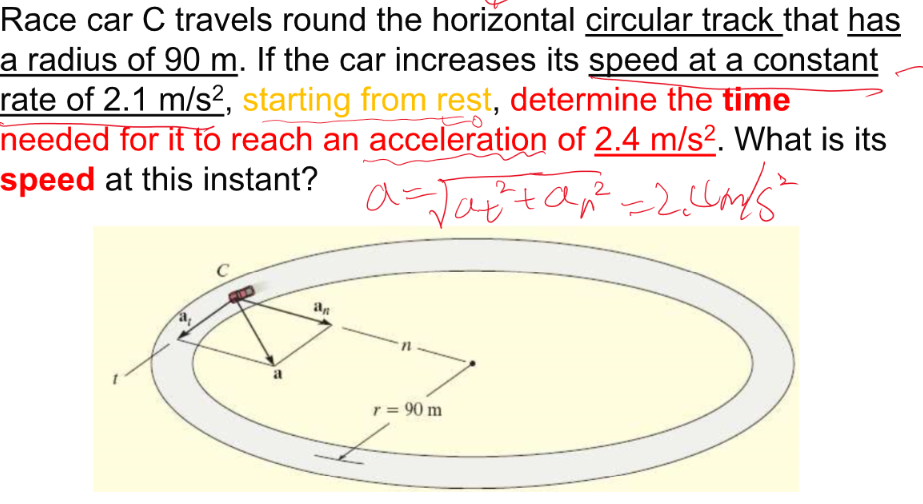
r = 90, at = 2.1, v0 = 0 가 주어지고, a = 2.4일 때 이므로 an을 구하는게 목표네요
an = v^2 / r 이므로 v를 구할 수 있고, at가 있으니 그것을 통해 속도를 구할 수 있겠네요

v = 6, at = 2, x = 10, y = 5 다 주어졌으니 속도의 각은 식을 미분해서 arctan을 통해 구합니다.
r 은 식 미분해서 얻는 값, 미분 한번 더 해서 얻는 값을 사용한 식을 통해 구하고, v가 주어졌으므로 an을 구해서 크기, 각 모두 구할 수 있습니다.

r, v가 주어지고, t =10일 때의 보트의 속도와 가속도를 구하면 된다.
vt는 t만 대입하면 바로 나오고, at 는 vt미분하면 끝, an은 v^2/r하면 끝이니 금방 나온다.

a가 t에 관한 식으로 나왔으니 적분해서 v, s 모두 구할 수 있다.
그럼 an도 구할 수 있으니 뚝딱 구할 수 있다.

theta, r 모두 t에 관한식으로 나왔으니 각각 미분해서 t만 집어 넣으면 금방 나온다.
그리하여 v,a 모두 구할 수 있다.

r'이 constant하다고 나왔으니 r''은 0일 것이다.
theta는 t에 관한 식으로 나와 있으므로 미분해서 전부 구할 수 있다.
z는 t로 미분해서 각각 식 마지막에 넣기만 하면 된다.

theta = 180일 조건이고, r이 theta에 대한 식으로 나와 있으므로 r을 미분하여 구하면 된다.그럼 식이 나올 것이고, 그 식에서 theta의 1차 미분, 2차미분 전부 구할 수 있다.

각도가 45도로 나와있다.
그럼 각각의 속력을 x,y 방향으로 분해해준뒤, Train이 기준이 되므로 A를 빼서 구하면 된다.
각도는 항상 arctan을 통해서 구할 수 있다.

여기선 B한테 at만 있는 것이 아닌 an이 있다는 것을 기억해야 한다.
회전 반경을 그냥 주지 않는다.

이 것도 동일하게 i, j로 나눠서 B에 A를 빼주면 구할 수 있다.
B의 가속도는 회전 반경을 잘 생각해서 구하면 된다.


m, F, k, s가 다 주어져 있다.
이 것을 통해서 FBD를 그리고, 수직항력을 구할 수 있다.
그럼 a도 잘 구할 수 있습니다.

acceleration이 constant하다고 했으니 가속도를 구할 수 있습니다.
그럼 FBD를 그려서 수직항력 먼저 구해주고, 마찰력까지 포함시켜주면 끝입니다!

위의 문제와 동일한 문제입니다.
FBD를 그려서 수직항력 먼저 구해주고, 그 것을 마찰력에 넣어서 잘 계산하면 가속도가 나옵니다.
그럼 3초 뒤에 속도를 구하면 되니까 3 곱하면 끝

여기선 A가 tention을 두배 받고, B가 A의 가속도의 반대 방향으로 2배라는 것만 생각하고 풀면 됩니다.
A,B각각의 FBD를 그리고 풀면 식 2개, 미지수 2개이므로 답이 나오게 됩니다.

A,B,C 모두 mg를 작성해놨고, F를 주어졌으니 ABC 전체의 가속도를 구할 수 있습니다.
그 뒤에 A만 따로 때서 구하면 Tension을 구할 수 있습니다.

속도, r를 토대로 at와 an을 구해줍니다.
그리고 수직 방향이므로 중력을 포함해서 FBD를 구하고, 답을 구하면 끝!

v가 정해졌고, at= 0이네요
그럼 an만 구하면 끝이기에 회전 반경을 위 식과 같이 미분해서 구하면 an를 구할 수 있습니다.
그럼 중력과 수직 항력만 an방향이므로 그 둘의 합이 man으로 해서 구하면 수직 항력도 구할 수 있습니다.

여기도 위의 식을 통해 회전 반경을 구해서 an을 구할 수 있습니다.
그럼 a도 나와 있으니 at를 구할 수 있습니다. 그럼 다 써서 수직 항력, 마찰력을 다 구할 수 있습니다.

이 문제도 회전 반경 나와있고, 속도 나와있으니 an 구할 수 있습니다.
tension, 중력이 man 해서 풀면 풀립니다.

m, r, theta가 주어졌다. 그럼 ar, atheta를 구할 수 있다.
그럼 FBD를 그려서 중력, arm의 힘, 수직항력을 그리고 다 풀어내면 된다.

r, theta, m 이 구해졌으니 위와 동일한 방식으로 구하면 된다.

여기도 m, r, theta가 다 나와있으니 위의 방식대로 풀 수 있습니다.
psi는 r / (dr / dtheta)를 통해 구해서 ar과 at의 각도를 구할 수 있습니다.
그럼 psi를 통해서 수직 항력의 ar과의 각도를 구할 수 있고, FBD를 풀면 끝입니다.

mg가 나와있고, 각도, 마찰력이 나와있습니다.
이 것을 통해서 FBD를 그리고, 수직항력을 구합니다.
FS = mv^2을 통해서 나머지를 풀면 됩니다.

여기서 Fs = mv^2을 사용할 때 Fs에는 위치와 스프링 둘다 들어가네요
그리고 v는 둘 다 0이니 h를 구할 수 있습니다.


B,A가 모두 연결되어 있으니 B가 2m/s라면 A는 -8m/s고 B가 b만큼 움직였다면 A는 -4b만큼 움직이므로 이 것을 통해 Fs = mv^2을 풀면 끝

m, 효율이 정해졌으니까 FBD를 통해 줄의 tension을 구할 수 있다. 그리고 속도, 가속도도 나와있으니 그대로 곱하고, 효율의 역수를 구하면 power를 구할 수 있다.

이 문제도 위 문제와 동일하게 풀면 끝난다.

에너지 보존 법칙을 활용하여 B 상태일 때 속도를 구할 수 있다.
그럼 속도와 회전 반경을 알 고 있으므로 an을 구할 수 있고, 그럼 tension을 구할 수 있다.

T(운동 E) + V(위치, 스프링) = T + V를 통해서 식을 구하면 다 풀 수 있다.
'기타' 카테고리의 다른 글
| 역사와 한국의 영토 10주차 - 독도 영유권 (2) | 2024.11.06 |
|---|---|
| 역사와 한국의 영토 9주차 - 해방 이후의 독도 (1) | 2024.11.06 |
| 동역학 7주차 정리 (0) | 2024.10.22 |
| 역사와 한국의 영토 중간고사 요약 (1) | 2024.10.21 |
| 역사와 한국의 영토 7주차 정리 및 퀴즈 (1) | 2024.10.13 |