Q. 다음 문장의 빈칸에 적절한 용어를 생각해 보세요.
"자동차의 성능을 나타내는 수십 가지의 특징들 중에서 20가지를 고려하면
데이터는 20차원의 벡터로 표현된다.이처럼 높은 차원의 데이터는 계산하는 데 시간이 많이 걸릴 뿐만 아니라
사람이 쉽게 이해할 수 있도록 시각화하는 것도 어렵다.높은 차원의 데이터를 원래 데이터의 특성을 크게 변화시키지 않으면서
낮은 차원의 벡터로 표현하고자 하는 기술을 ( 차원 줄이기(Dimensionality Reduction) )라고 한다."
1차시 - 차원 줄이기의 목적

높은 차원의 데이터를 낮은 차원 데이터로 바꾸는 것 -> 차원 줄이기



차원 줄이기는 비지도 학습 중 한가지 이다.

데이터들의 상관관계가 높아야 압축할 수 있다. redundant 가 높다!
소수점이 생략되거나 도구의 문제로 일렬이 아니다.

높은 상관성을 가진다 => 높은 중복성을 가진다.


적성이라는 하나의 데이터로 변환한다.
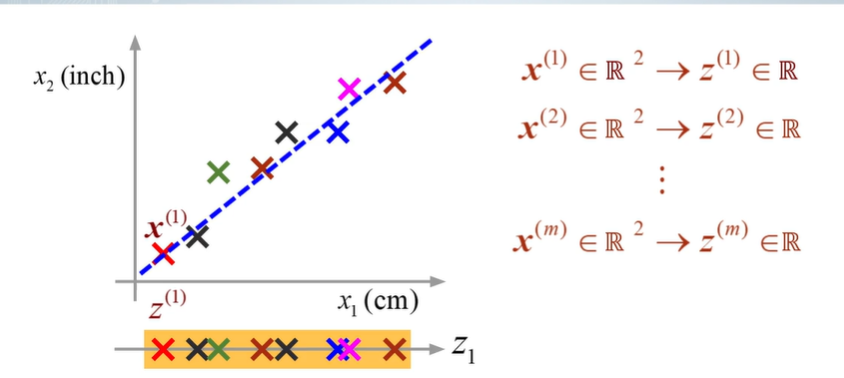
1차원 데이터로 변환!
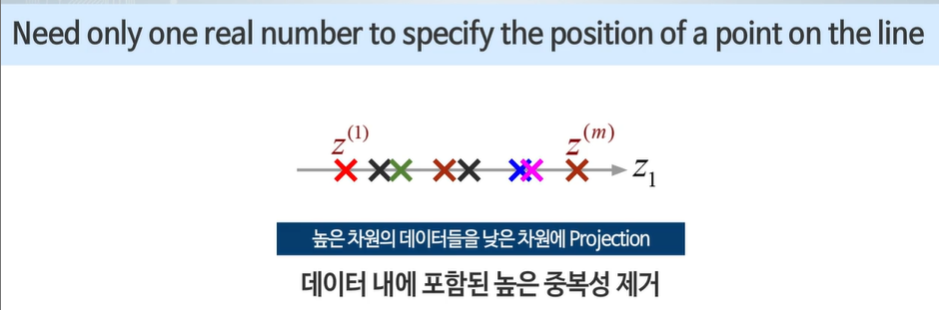
주어진 데이터들을 새로운 축으로 옮긴다!
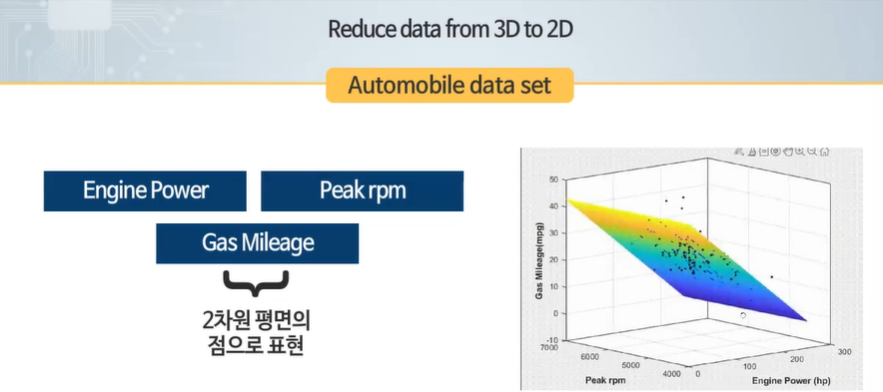
데이터 압축의 목적 - 데이터의 정보량은 줄이지 않으면서 용량을 줄인다. 학습알고리즘의 속도 향상
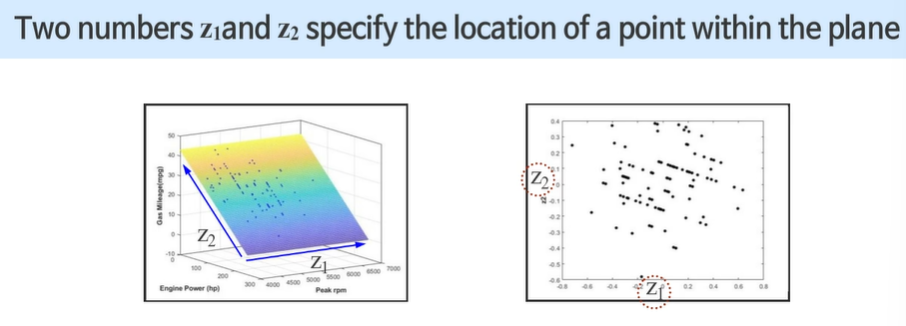
3차원 공간 상의 벡터를 2차원 공간 상의 벡터로 변환하였다.
데이터 시각화 - 높은 차원의 데이터들을 2,3차원에 표현할 수 없다.
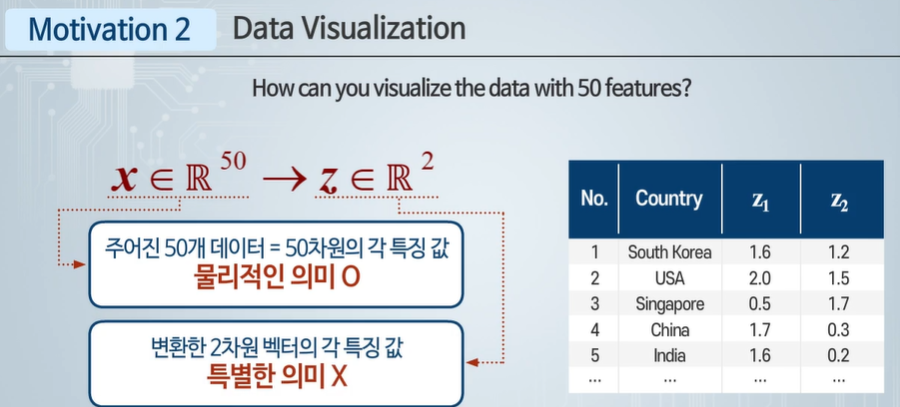
50차원 벡터를 2차원 벡터로 변환한다.
시각화만 할 뿐이고, 의미를 생각하면 안 된다.
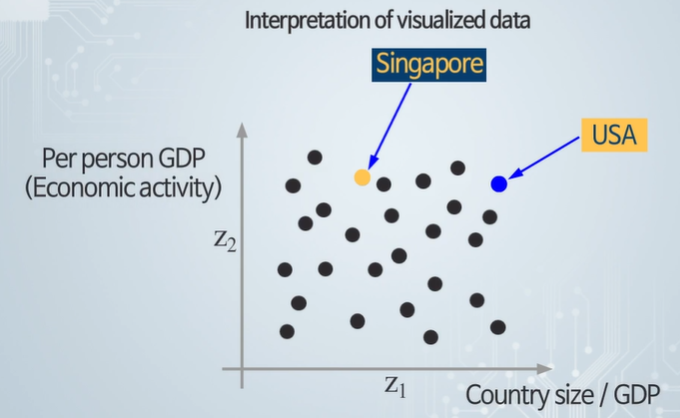

2차시 - Principal Component Analysis


평균값 정규화 - 데이터의 평균으로 빼주어 평균을 0으로 만들기

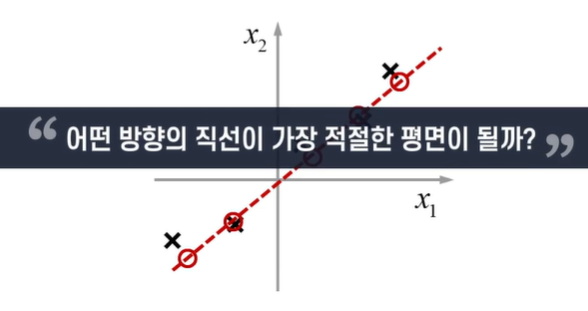
데이터로부터 수직이 되는 선을 그어 옮긴다!
직선에 투영시킨 거리가 작을수록 가장 좋은 Projection이다.

이건 거리가 너무 멀다.

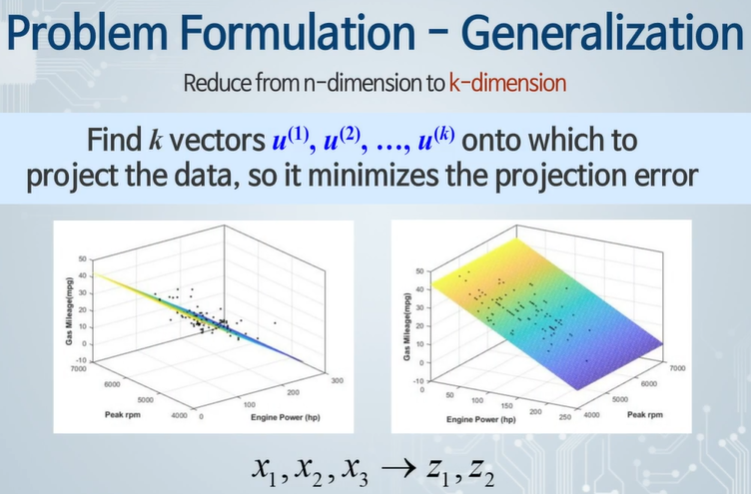
3차원 공간상의 점을 2차원으로 줄인다.
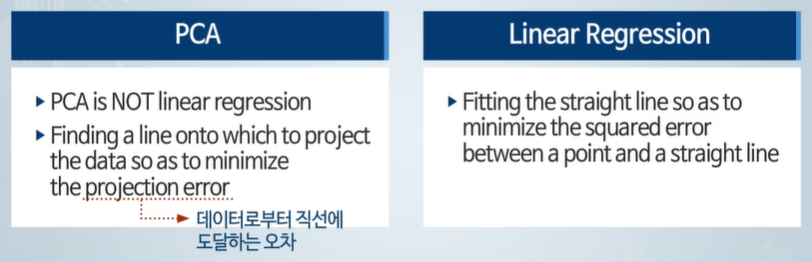
PCA는 선형회귀가 아니다. 직선에 도달하는 오차를 줄인다.
선형회귀는 직선의 방정식을 찾아서 데이터에 적합화 시킨다. - 제곱 최소 오차를 최소화한다.
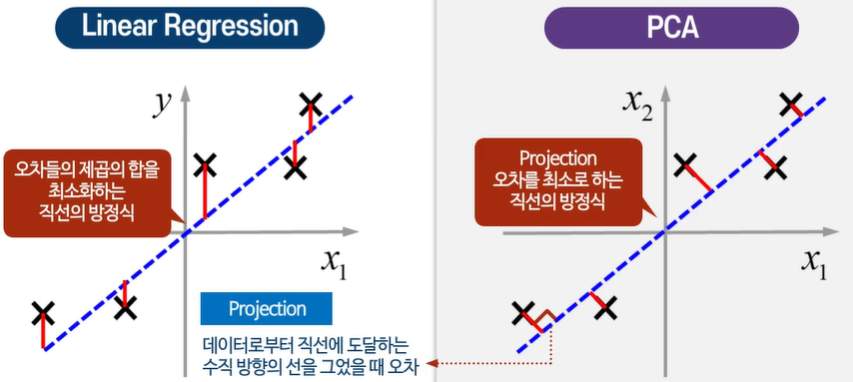
선형회귀에 있어서의 오차와 PCA에서의 오차는 다르게 정의된다.

3차시 - PCA알고리즘


몇 가지 전처리를 진행해야 한다.
평균값을 구한 뒤 각 데이터에 빼준다. -> 평균이 0으로 만들어진다.


서로 다른 크기를 가지고 있는다.
-> 그대로 적용하면 큰 값들이 지배적이게 된다. -> 스케일링한다.

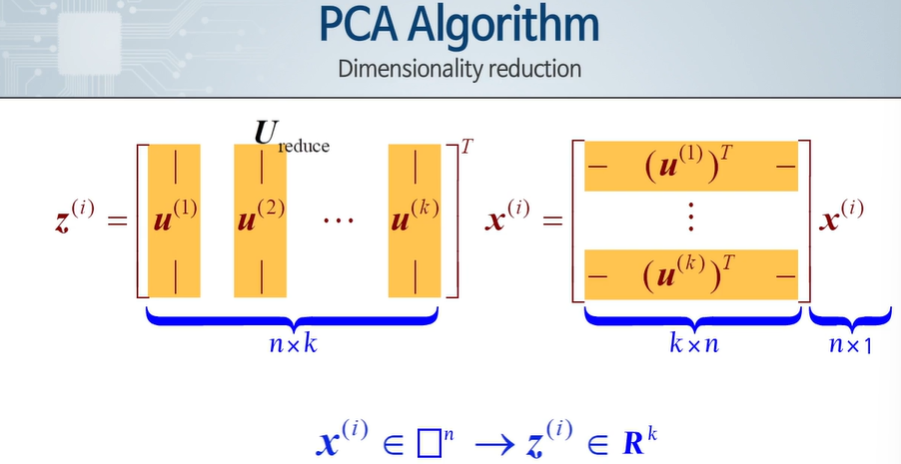
2차원 x를 1차원 z로 변환한다.
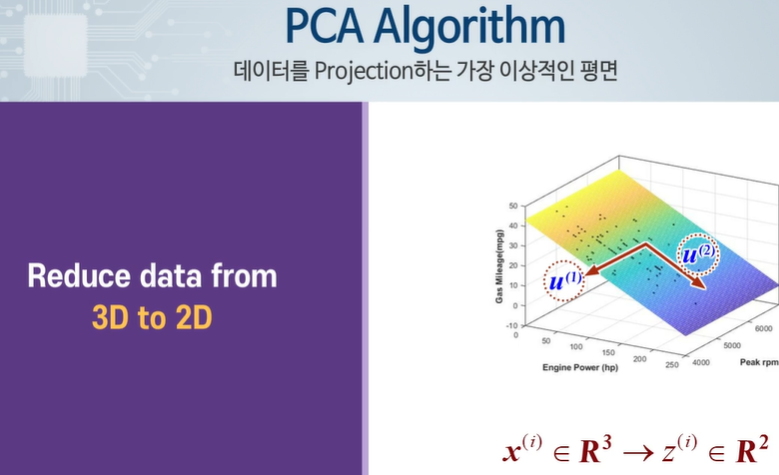

일반적으로 n차원 데이터를 k차원으로 바꾼다.
상관 행렬을 그리게 된다. - 정사각 행렬이고, 대칭행렬이다.(역행렬을 곱하기 때문)






4차시 - Principal Component 수의 결정



가장 작은 값이 되는 k를 사용하면 된다.


조건을 만족할 때까지 반복해서 만족하는 k가 가장 적절한 값이다.
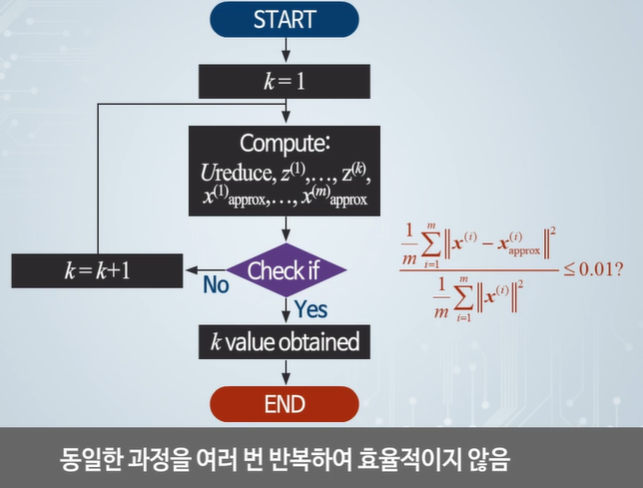
동일 계산을 너무 반복해야 한다.
효율적인 방법은? -> S를 사용한다.



95%의 variance가 보존되어있다고 볼 수 있다.
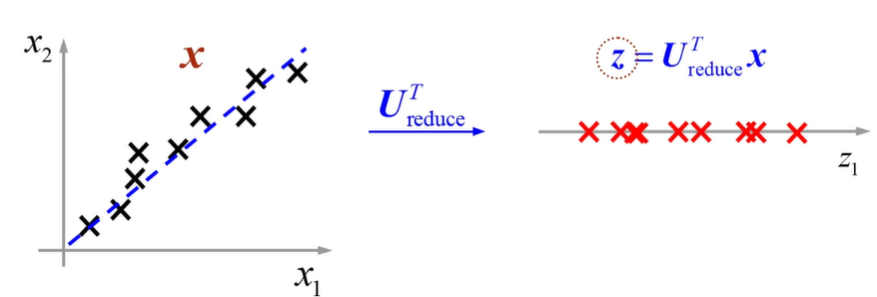
복원 과정! - approx를 이용해 근사화한다.
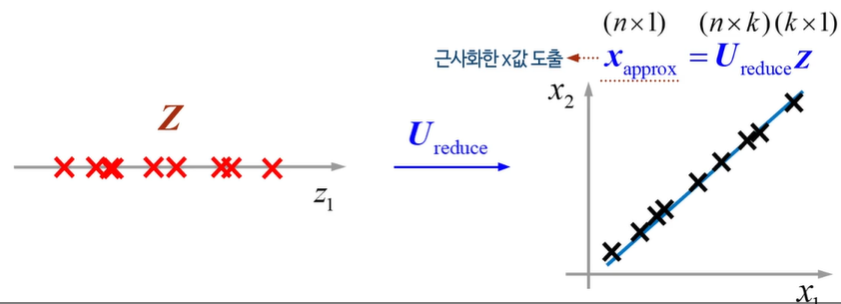
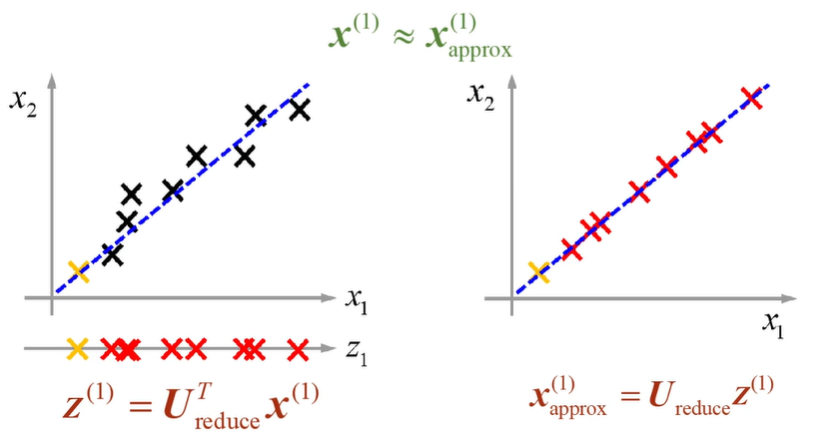
5차시 - PCA 적용 방법



입력 이미지라면 데이터 차원이 어마 무시하게 커진다. -> 계산량이 엄청나게 늘어버린다.


테스트 데이터 또한 동일하게 압축해야 한다.


정보량은 저하시키지 않으면서 사이즈만 줄이기!
속도를 올릴 수 있다.

널리 사용되긴 하는데 잘못 사용하는 경우도 있다.

특징 값이 줄었으므로 오버피팅이 줄 것이라고 생각할 수 있다.
-> 그러나 올바른 사용법이 아니다.

문제는 없어 보이지만 PCA는 x 데이터에 대해서만 적용하기 때문이다.

정규화를 사용해야 한다!



PCA도 시간이 걸리는 작업이고, 오차가 나올 수밖에 없다.

'인공지능 > 공부' 카테고리의 다른 글
| 생성형 인공지능 입문 13주차 - Transformer 기반 action 생성 (1) | 2024.05.27 |
|---|---|
| 모두를 위한 머신러닝 13주차 퀴즈 (0) | 2024.05.27 |
| 생성형 인공지능 입문 - 12주차 퀴즈 (1) | 2024.05.20 |
| 생성형 인공지능 12주차 - 분산 기반 영상 생성 (0) | 2024.05.20 |
| 모두를 위한 머신러닝 과제2 - k means 진행, 계산 (0) | 2024.05.20 |