20200323

노드 당 자유도 * 노드 수 = K matrix 행과 열의 길이
1. K element 만들기
2. assemble 해서 k matrix 만들기
3. boundary condition
4. kd = F 풀기
5. ub, Fa 풀기!!

문제 푸는 Matlab 코드입니다.
% step 1 : element stiffness matrices generation
k = 200
ek1 = [k , -k; -k, k];
ek2 = ek1
ek3 = ek2
ek4 = ek3
% step 2 : assemble
tdof = 5
K = zeros(tdof);
K([1,2],[1,2]) = K([1,2],[1,2]) + ek1 ;
K([2,3],[2,3]) = K([2,3],[2,3]) + ek2 ;
K([3,4],[3,4]) = K([3,4],[3,4]) + ek3 ;
K([4,5],[4,5]) = K([4,5],[4,5]) + ek4 ;
% step 3 : B.C (displacement condition and Force)
dof_a = [1,5]
dof_b = [2,3,4]
Kaa = K(dof_a,dof_a);
Kbb = K(dof_b,dof_b);
Kab = K(dof_a,dof_b);
Kba = K(dof_b,dof_a);
ua = [0 0.02]'
Fb = [0,0,0]'
% step 4 : solve
ub = inv(Kbb)*(Fb - Kba * ua);
% step 5
Fa = Kaa * ua + Kab * ub경계 조건을 넣어주지 않으면 det가 0으로 역행렬이 존재하지 않습니다!
K matrix를 만들 때 for문을 이용하여 불필요한 반복을 막을 수 있습니다.
Element- dof connectivity를 만들어야 합니다 == etable
| Element | dof |
| 1 | 1,2 |
| 2 | 2,3 |
| 3 | 3,4 |
| 4 | 4,5 |
etable = [1,2;2,3;3,4;4,5];
for i 1:4
edof = etable(i,:);
K(edof,edof) = K(edof,edof) + ek1
% ek가 다 동일하기 때문에 이렇게 작성이 가능하다
end
1. Linear elastic problems로 K matrix가 summetric이다.
2. K는 바운더리 컨디션이 없으면 역행렬이 없다.
3. The main diagonal componente are positive
4. nonzero vector x는 xt l x >= 0이다
Potential energy approach
Porential energy를 최소화하는 방향으로 진행한다.
The principal of minimum poential energy
=> of all the geometrically possible shapes that a body can assume, the true one, corresponding to the satisfaction of stable equilibrium of the body is identified by a minimun poential energy
평형 조건을 만족시키는 변형은 포텐셜 에너지가 최소화되는 방향으로 진행한다!
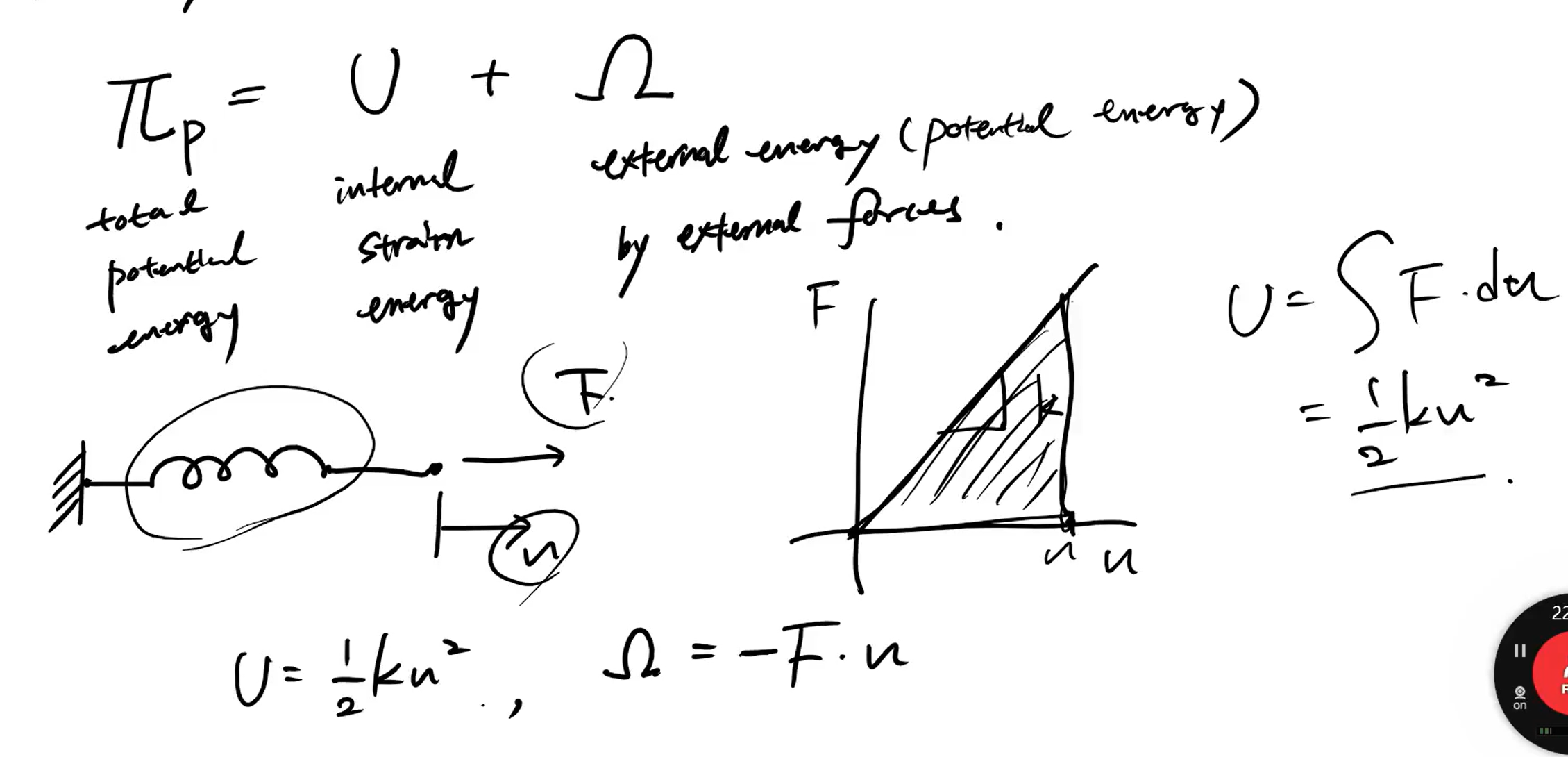
external energy는 항상 음수이다!!
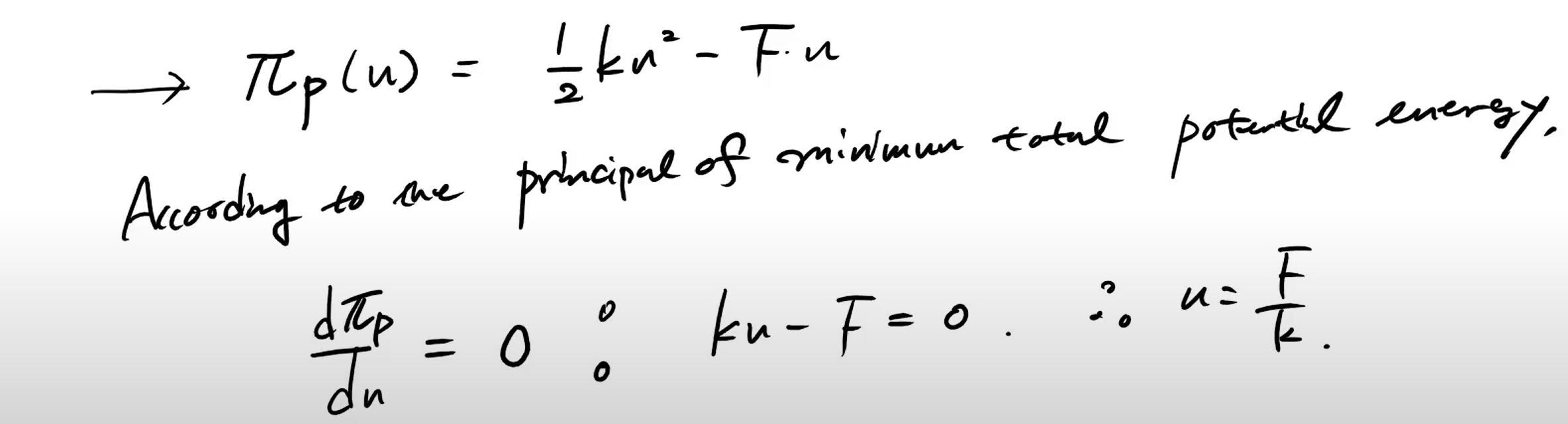
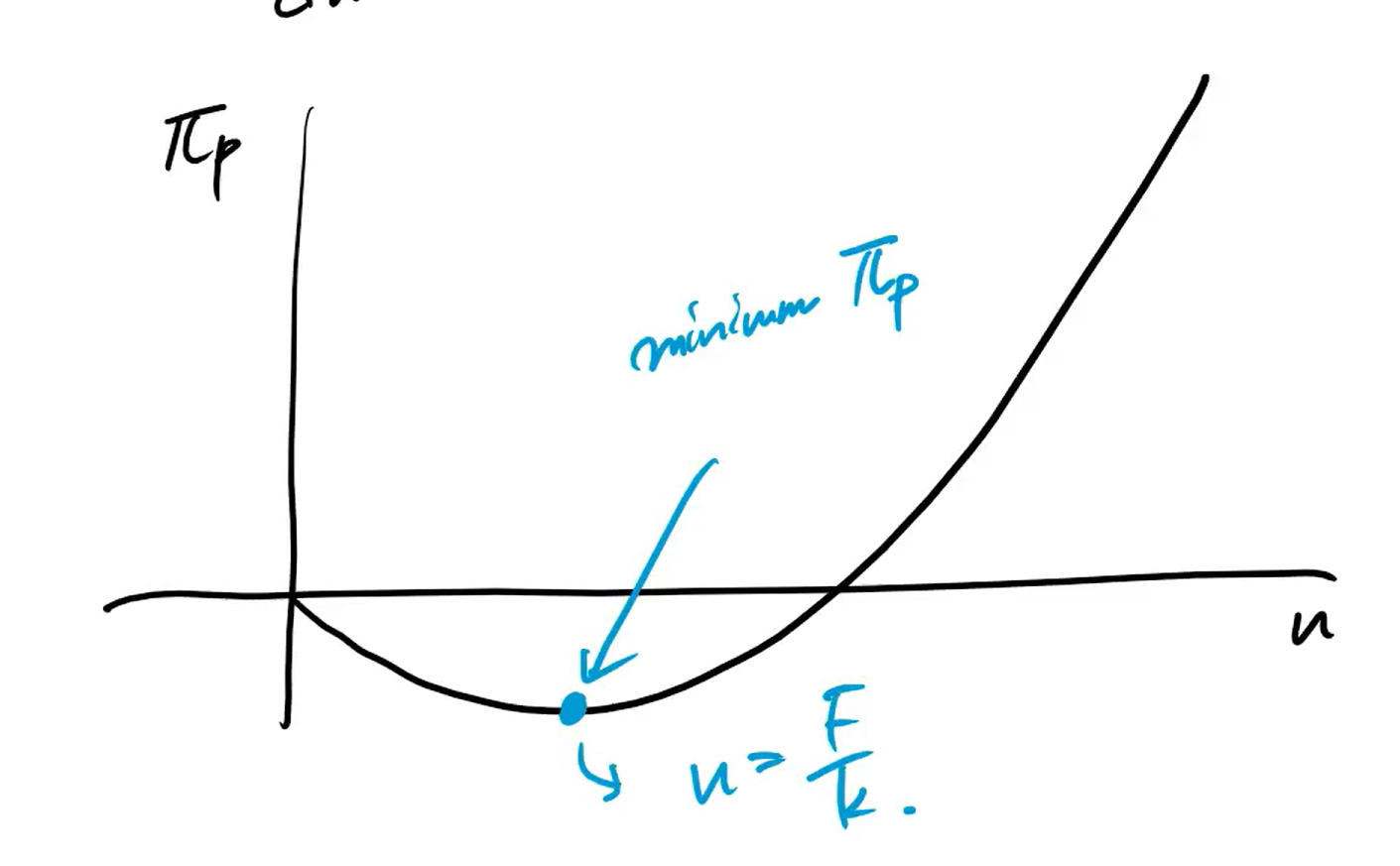
여기에서 최소가 되는 것이다!
여기선 자유도가 1개다
여러개가 된다면...?

모든 자유도 지점에서 0이 되어야 한다.
u를 d로 잘 못 작성해서 변경하였습니다.
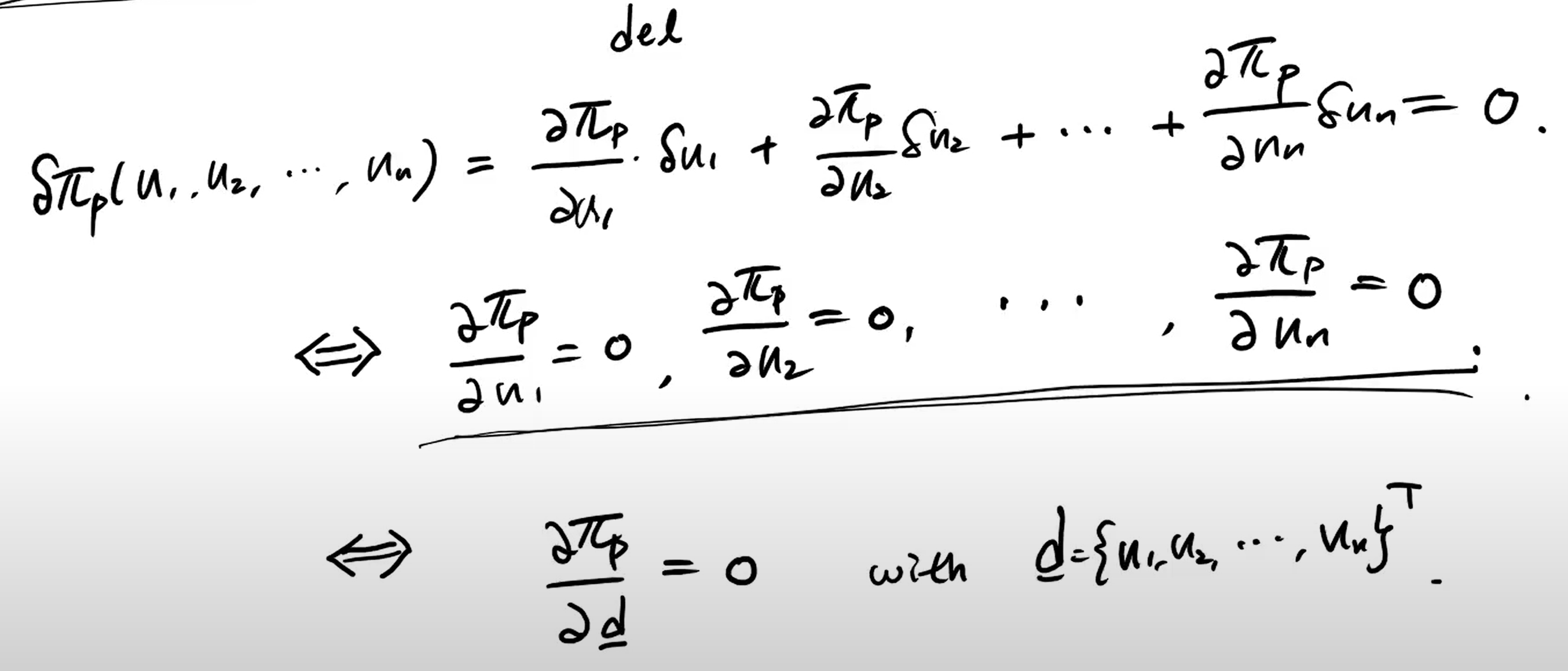
'FEM > 기본개념' 카테고리의 다른 글
| FEM, 유한 요소 초반부 kd = F (2) | 2024.08.07 |
|---|