이전에 받았던 일을 다시 진행하게 되어 조금만 정리 하겠습니다..
20200316
FEM - 컴퓨터를 이용해 구조 해석(고체, 동)을 진행하여 디자인을 하는 과목
PDE - 수학적으로는 전부 미분 방정식을 푸는 문제이다
구조에 힘을 주면 변형(deformed shape)이 일어난다- 탄성 영역에서만 공부한다.
변형체는 스프링으로 볼 수 있다. stiffness Method == Spring element
k = spring constant = spring stiffness = 강성
u = displacement
F = Force
F = ku
구조 하나하나를 쪼갠 것 = element
절점들 = nodes
이렇게 하나하나 나누게 되면 백터와 메트릭스로 변하게 된다.
스프링!!!
K == stiffness
ku = F - matrix와 vector로 구성된다. == system equation (discretized == 이산화 되었다.)

Spring element는 node 2개와 1개의 k로 이루어 졌다.
그럼 변위도 u1, u2가 있고, 힘도 f1, f2(internal force == 내력)가 있다.

이 그림은 ku=F 식에 의하여 아래와 같이 된다.

이제 이 식 2개를 행렬식으로 변화할 수 있다.

k메트릭스를 Element stiffness matrix라 부른다. -> ke
u 벡터는 Element displacement vector라 부른다. -> de
f 벡터는 Element force vector라 부른다. -> fe

element 레벨에서의 식이다 = discretized equillibrium equation in an element level
스플링이 여러 개라면! == Assemblage

여기서 P는 외력(external)이다 -> 힘이 평형이 되어야 한다. -> node1을 fix하였다.
정역학적으로는 평형 상태가 되었따
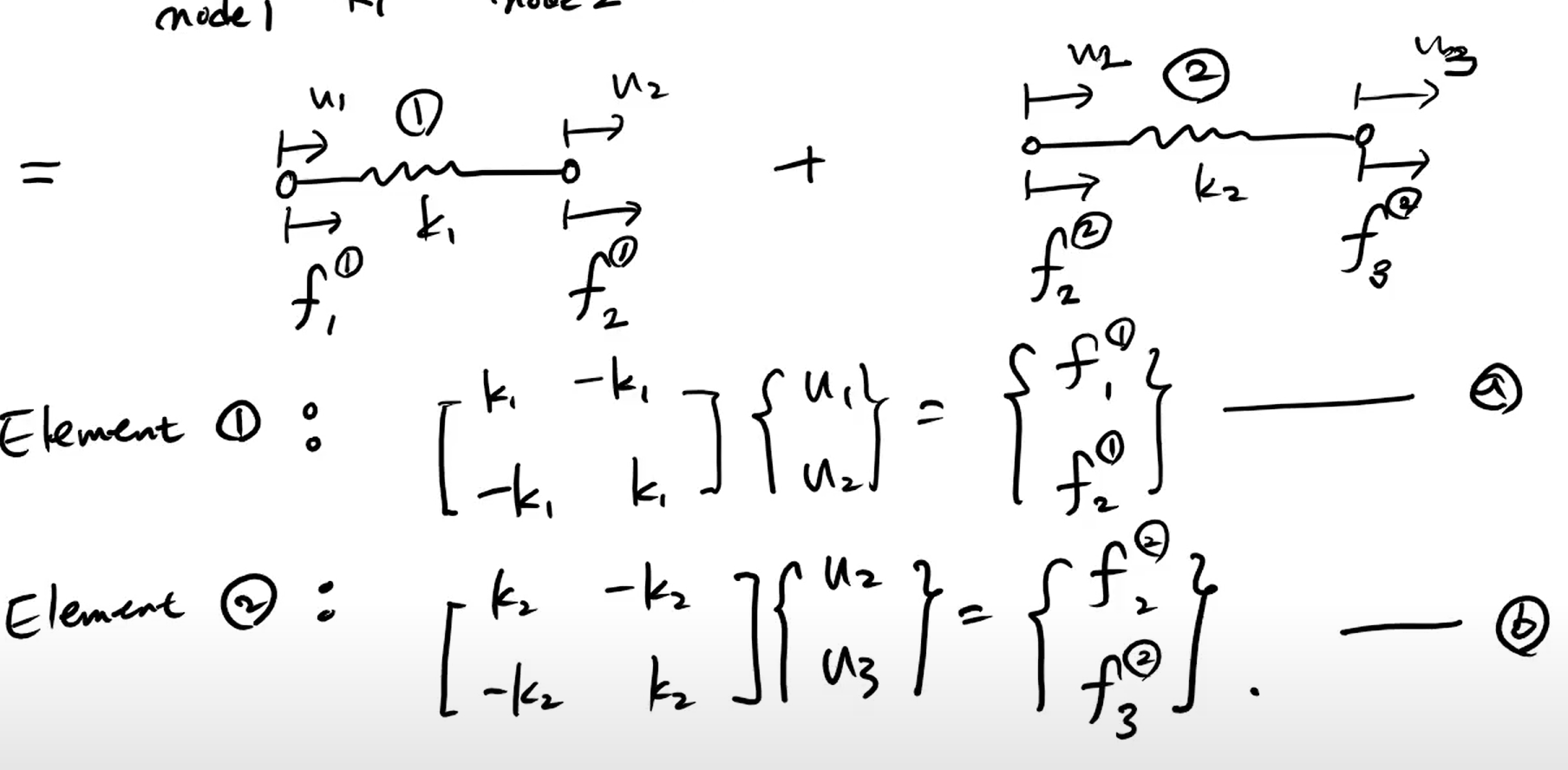
식 a와 b는 다시 정리할 수 있다.
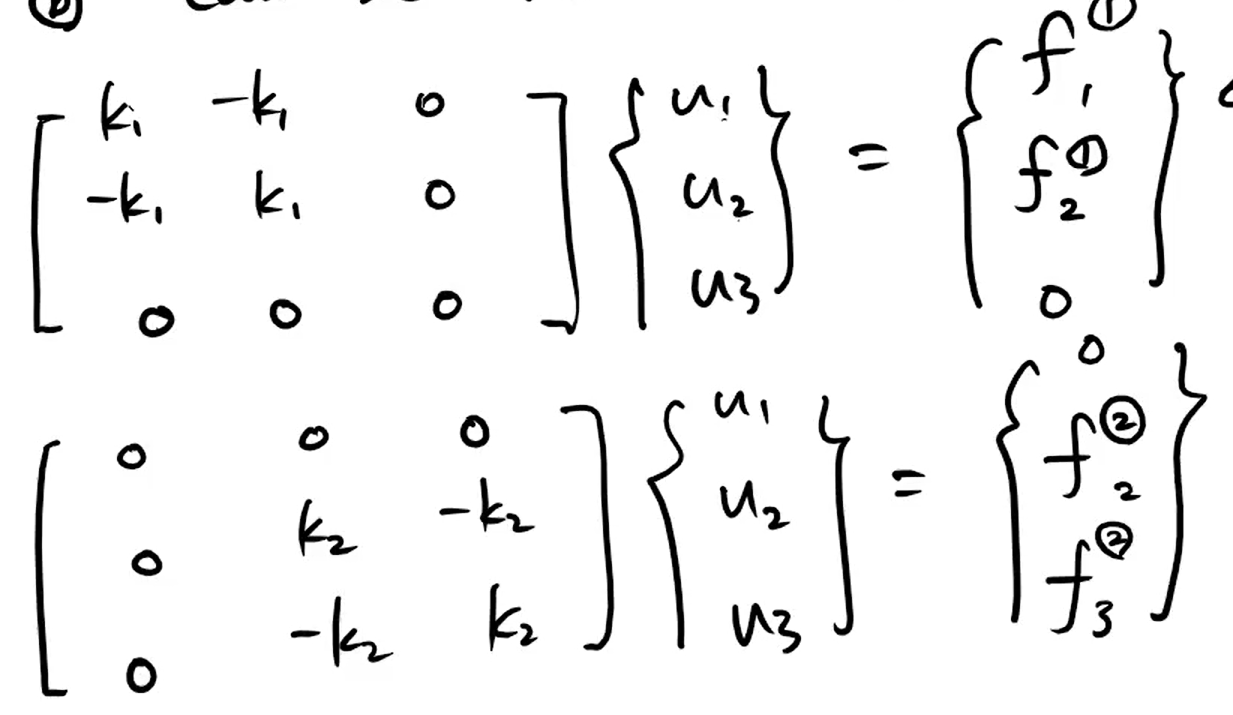
이 두 행렬을 더한다! == Assemble

두 식을 더하면! k, u, f로 정리된다.

더할 때 단순히 더하는게 아닌 assemble하여 행렬 크기가 커진다.

Global force vector는 external force이다!
2번째 노드는 두 힘이 더해져서 0이 되는 장소이다!
첫번째 노드는 계산을 통해 구해야 한다. = unkwon reaction force
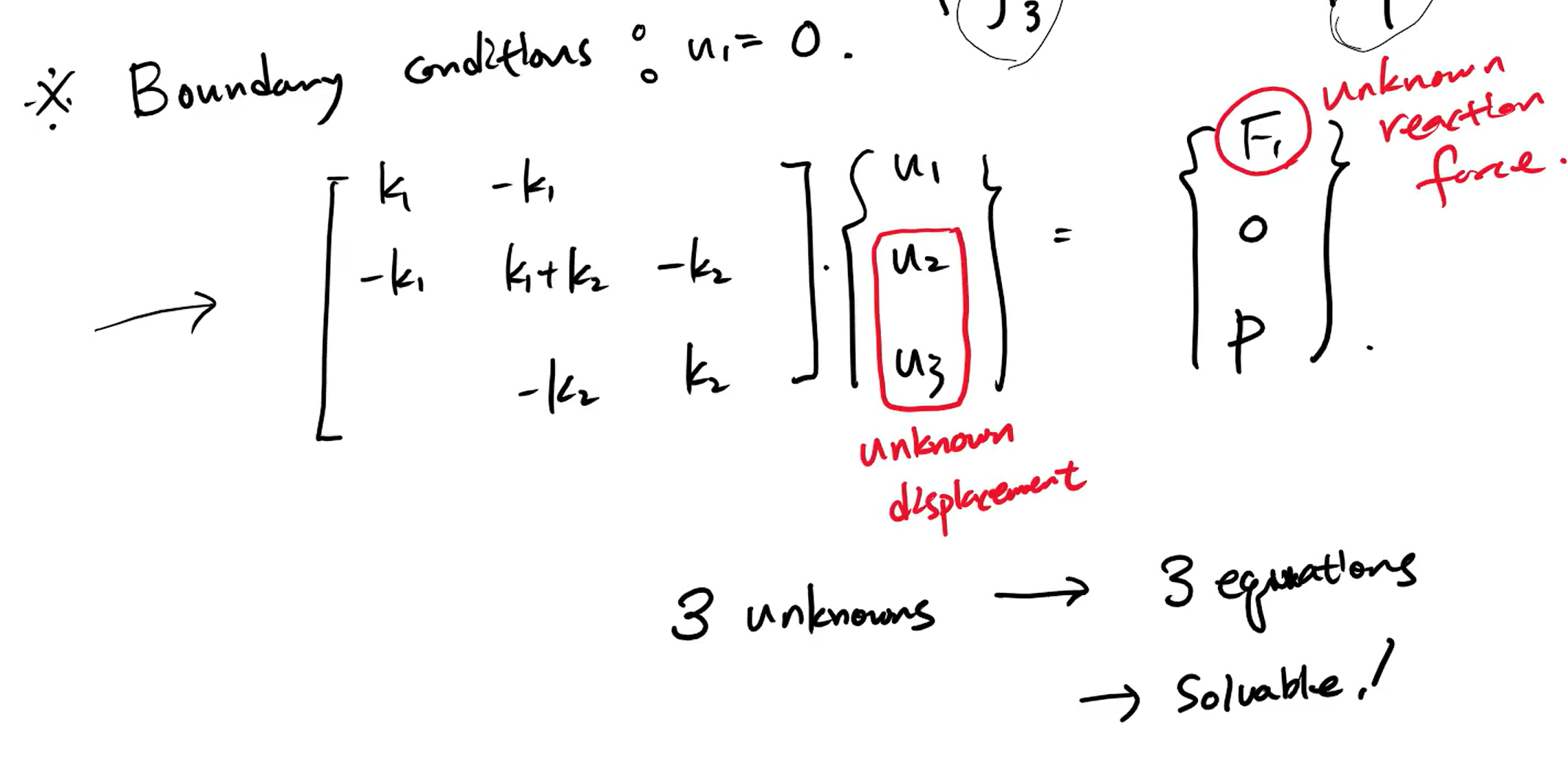
경계조건으로 인해 u1 = 0가 된다! -> u2, u3는 모른다.
행렬 계산으로 풀 수 있다.
u는 앞으로 degree of freedom 즉 자유도(dof)이다. -> k메트릭스는 각각의 자유도로 채운다.
스프링 문제는 1노드당 1자유도 문제이다. -> k matrix가 n*n 크기이다.
Boundary Condition
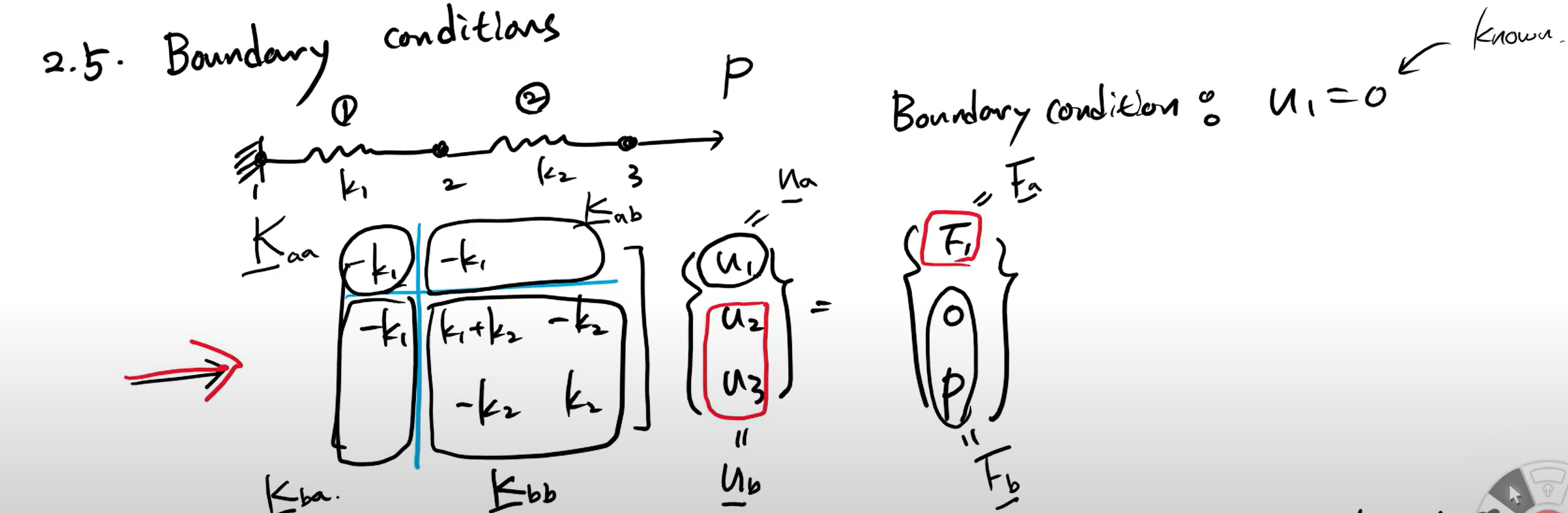
k,d,F 를 서브 메트릭스, 벡터로 다 쪼갠다.
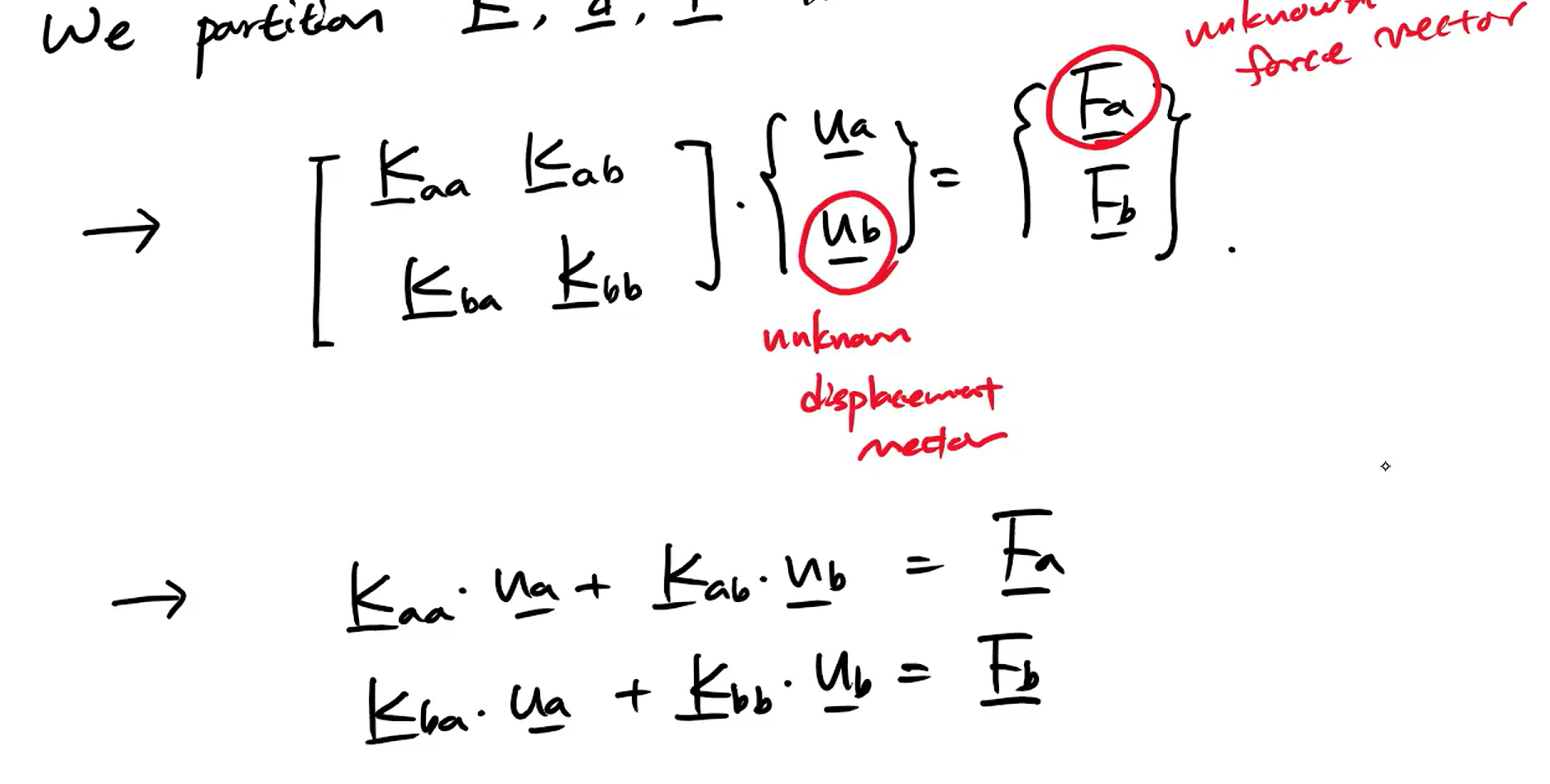
위 식은 정리해서 unknown을 다 구할 수 있다.


이렇게 구할 수 있다.
연습문제


k matrix를 만들면 위와 같이 진행된다.