Debiasing Recommendation with Personal Popularity 리뷰

https://arxiv.org/html/2402.07425v2

Debiasing Recommendation with Personal Popularity

 

저 빼기가 왜 저렇게 되는지는 모르겠다...?

 

 

 

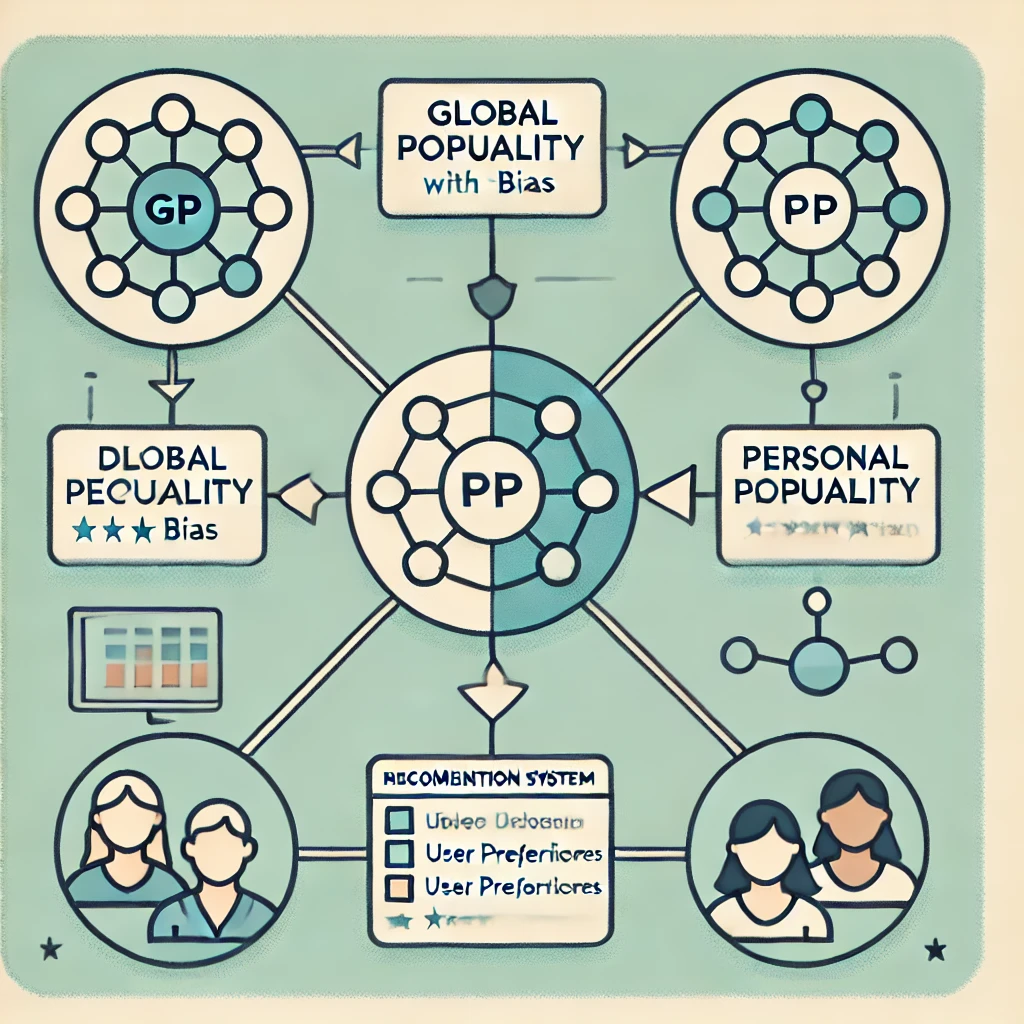
논문 "Debiasing Recommendation with Personal Popularity"는 추천 시스템에서 전통적인 글로벌 인기(Global Popularity, GP) 편향을 해결하기 위한 새로운 접근 방식을 제안합니다. 이 논문에서는 개인화된 추천을 개선하고, 다양한 사용자 경험을 제공하기 위해 "개인 인기(Personal Popularity, PP)"라는 새로운 개념을 도입했습니다.

문제 정의

추천 시스템은 사용자의 행동을 분석하여 개인화된 추천을 제공하는 것을 목표로 하지만, 기존의 많은 추천 시스템은 전 세계적으로 인기 있는 항목을 과도하게 추천하는 GP 편향을 가지고 있습니다. 이 편향은 사용자의 개인적인 취향을 제대로 반영하지 못하고, 결과적으로 사용자 경험과 추천의 정확성을 저해할 수 있습니다. 이 문제를 해결하기 위해 GP를 고려한 기존의 편향 감소(debiasing) 방법들이 제안되었지만, 이들은 모든 사용자에게 동일한 인기도 세트를 사용하는 글로벌 관점을 바탕으로 하고 있어 개별 사용자의 관심사를 충분히 반영하지 못했습니다.

연구의 목표

논문은 사용자별로 개별적으로 인기가 있는 항목을 식별할 수 있는 "개인 인기(PP)" 개념을 제안하고, 이를 통해 글로벌 인기 편향을 완화하며 개인화된 추천을 개선하는 것을 목표로 합니다. PP는 사용자 간의 유사성을 고려하여 각 사용자에 대해 다른 인기 항목 세트를 도출함으로써, 사용자 개별의 취향을 반영하는 것을 가능하게 합니다.

제안한 방법

PP를 추천 시스템에 통합하기 위해, 저자들은 "개인 인기 인식 반사실적(PPAC) 프레임워크"를 제안했습니다. 이 프레임워크는 기존의 추천 모델에 쉽게 적용할 수 있으며, PP와 GP의 직접적 및 간접적 효과를 반사실적 추론(counterfactual inference) 기법을 사용하여 조정함으로써 편향 없는 추천을 제공합니다. 이 프레임워크의 핵심 요소는 다음과 같습니다:

1. 사용자 유사성 측정: 사용자 간의 유사성은 그들의 상호작용 항목 세트의 겹침 정도로 정의됩니다. 이는 자카드 유사도(Jaccard Similarity)를 기반으로 계산됩니다.
2. 개인 인기(PP)의 정의: 특정 사용자와 유사한 다른 사용자들 사이에서 특정 항목의 인기를 측정하는 방식으로 정의됩니다. 수식으로는 다음과 같이 나타낼 수 있습니다:
   pu,i=∣Sui∣/∣Su∣​
   여기서 Sui는 사용자 u와 유사한 사용자들 중에서 항목 i와 상호작용한 사용자들의 집합입니다.
3. 반사실적 추론 기법: PP와 GP가 추천 점수에 미치는 직접적인 영향을 조정하기 위해 반사실적 추론을 사용합니다. 이 과정에서, GP와 PP가 결합된 프록시 변수 X를 도입하여 이들의 영향을 추정합니다.
4. 모델 학습 및 추론: PPAC 프레임워크는 기본 모델(예: MF, LightGCN)의 예측 점수에 PP와 GP를 조정하여 편향을 완화합니다. 최종적으로는 반사실적 세계에서의 조정을 통해 사용자에게 더 정확하고 개인화된 추천을 제공합니다.

연구 결과

저자들은 PPAC 프레임워크를 다양한 데이터셋과 기본 모델에 적용하여 실험을 수행했고, 그 결과 모든 기존의 편향 감소 방법보다 뛰어난 성능을 보였습니다. 특히, 회수율(Recall)과 NDCG에서 최대 46.8%와 61.9%의 성능 향상을 달성했습니다. 또한, 실험 결과 PPAC가 글로벌 인기 항목의 추천 빈도를 효과적으로 줄이면서도, 사용자의 진정한 선호도를 더 잘 반영하는 추천을 할 수 있음을 확인했습니다.

한계점

이 논문은 PPAC 프레임워크의 설계 및 평가에서 뛰어난 성과를 보였지만, 몇 가지 한계점이 존재합니다. 첫째, 개인 인기는 사용자 간의 유사성에 크게 의존하므로, 데이터셋이 부족하거나 사용자의 유사성이 제대로 측정되지 않는 경우 PP의 효과가 떨어질 수 있습니다. 둘째, 이 연구에서는 반사실적 추론을 통해 PP와 GP의 직접적인 영향을 조정하는 방식을 제안했지만, 이 과정에서 복잡한 계산이 필요하며, 실시간 시스템에 적용하는 데 시간이 소요될 수 있습니다. 마지막으로, 논문에서 제시한 PP 정의와 모델링은 단순한 협업 필터링 설정을 기반으로 하지만, 더 복잡한 시나리오에서는 확장성이 부족할 수 있습니다.

결론

논문에서 제안한 개인 인기(PP)와 PPAC 프레임워크는 기존의 글로벌 인기 편향 문제를 효과적으로 완화하며, 개인화된 추천의 정확성을 크게 향상시킬 수 있음을 입증했습니다. 이 연구는 향후 더욱 정교한 사용자 맞춤형 추천 시스템 개발에 중요한 기여를 할 것으로 기대됩니다

 

그럼 GP와 PP에 대해 좀 더 설명해주라
어떤 메커니즘인지, 주요한 차이와 각자의 장 단점이 뭔지 알려주라

Global Popularity (GP)와 Personal Popularity (PP) 메커니즘

Global Popularity (GP)

메커니즘:

• GP는 특정 항목의 전체 사용자 집단에서의 인기도를 측정하는 방식입니다. 즉, 전체 사용자 중에서 특정 항목과 상호작용한 사용자의 비율로 계산됩니다. 이 방법은 모든 사용자에게 동일한 인기 항목 목록을 추천하는 데 사용됩니다.
  여기서 Ui​는 항목 i와 상호작용한 사용자의 집합이고, ∣U∣는 전체 사용자 수를 의미합니다.

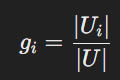
장점:

• 간단하고 직관적임: GP는 전체 사용자 기반에서 인기도를 계산하기 때문에 계산이 간단하며, 직관적으로 인기도가 높은 항목을 쉽게 식별할 수 있습니다.
• 많은 데이터를 활용: GP는 전체 사용자 집단의 데이터를 기반으로 하므로, 충분한 데이터가 있는 경우 일반적으로 신뢰할 수 있는 결과를 제공합니다.

단점:

• 개인화 부족: 모든 사용자에게 동일한 인기 항목이 추천되므로, 개인의 취향을 반영하지 못하고 다양한 사용자 경험을 제공하지 못할 수 있습니다.
• 편향 문제: GP에 의존할 경우, "매튜 효과(Matthew Effect)"가 발생할 수 있습니다. 즉, 이미 인기 있는 항목이 계속해서 더 많은 추천을 받으며 더욱더 인기를 얻게 되는 상황이 발생할 수 있습니다.

Personal Popularity (PP)

메커니즘:

• PP는 특정 사용자를 중심으로 그와 유사한 관심사를 가진 사용자 집단 내에서의 인기도를 측정합니다. 즉, 사용자 간의 유사성에 기반하여 각 사용자에 대해 개별적인 인기 항목 목록을 생성합니다. 이 유사성은 사용자가 이전에 상호작용한 항목들의 집합 간의 유사성을 통해 계산됩니다.
  여기서 Sui는 사용자 u와 유사한 사용자들 중에서 항목 i와 상호작용한 사용자들의 집합이고, ∣Su∣는 사용자 u와 유사한 전체 사용자 수를 의미합니다.

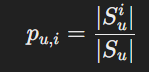
장점:

• 개인화된 추천: PP는 각 사용자의 개별적인 관심사를 반영하여 맞춤형 추천을 제공합니다. 이는 다양한 사용자에게 더 적합한 추천을 가능하게 하며, 사용자 경험을 향상시킵니다.
• 편향 완화: GP와 달리 PP는 각 사용자별로 다르게 계산되므로, 인기 있는 항목이 모든 사용자에게 추천되는 것을 방지하고, 더욱 다양한 항목이 추천될 수 있습니다.

단점:

• 복잡한 계산: PP는 사용자 간 유사성을 계산해야 하고, 각 사용자에 대해 별도의 인기 항목 세트를 생성해야 하므로 계산 비용이 높습니다.
• 데이터 의존성: PP는 사용자 유사성을 계산하는 데 충분한 데이터가 필요하며, 데이터가 부족하거나 부정확할 경우 추천의 품질이 저하될 수 있습니다.

주요 차이점

1. 관점의 차이:
   • GP: 전체 사용자 집단을 기준으로 항목의 인기를 측정합니다.
   • PP: 개별 사용자의 관심사를 반영하여, 그와 유사한 사용자들 사이에서 항목의 인기를 측정합니다.
2. 추천의 다양성:
   • GP: 모든 사용자에게 동일한 인기 항목을 추천하여, 추천 항목이 대부분 유사하게 나타날 수 있습니다.
   • PP: 각 사용자에게 맞춤형 추천을 제공하여, 추천 항목의 다양성을 높일 수 있습니다.
3. 계산 복잡도:
   • GP: 비교적 계산이 간단하며, 대규모 사용자 집단에서도 쉽게 적용 가능합니다.
   • PP: 사용자 간의 유사성을 지속적으로 계산해야 하며, 이를 기반으로 개별적인 추천을 해야 하므로 계산이 복잡합니다.

결론

GP와 PP는 추천 시스템에서 각기 다른 방식으로 사용자의 경험을 개선할 수 있는 중요한 메커니즘입니다. GP는 단순하고 직관적이지만, 개인화가 부족하고 편향 문제가 있을 수 있습니다. 반면에 PP는 개인화된 추천을 가능하게 하며, 편향을 완화하는 데 효과적이지만, 계산 비용이 높고 데이터에 크게 의존합니다. 각각의 메커니즘은 상황에 따라 적절하게 사용될 수 있으며, PPAC 프레임워크와 같이 두 메커니즘을 결합한 접근법이 추천 시스템의 성능을 극대화하는 데 유용할 수 있습니다.

 

논문에서 나온 반 사실적 추론 기법에 대해 잘 모르겠어
반 사실적 추론 기법이 무엇인지, 프록시 변수가 무엇인지, 어떻게 영향을 추정하는지, 이러한 방식을 써서 어떤 결과의 변화가 생겼는지, 연산 과정이 어떻게 되는지 알려주라 

반사실적 추론(Counterfactual Inference) 기법

개념 설명

반사실적 추론(Counterfactual Inference)은 실제로 발생한 사건과 다른 가상 시나리오에서 결과가 어떻게 달라질지 상상하고 분석하는 기법입니다. 이 기법은 인과 관계를 분석하고, 특정 변수의 변화를 통해 결과에 미치는 영향을 평가하는 데 사용됩니다. 반사실적 추론은 "만약 ~~였다면, 결과는 어떻게 달라졌을까?"라는 질문을 다룹니다.

논문에서의 사용

논문에서는 GP(Global Popularity)와 PP(Personal Popularity)가 추천 점수에 미치는 직접적 효과를 조정하기 위해 반사실적 추론 기법을 사용했습니다. 이 접근 방식은 기존의 추천 시스템에서 발생하는 글로벌 인기 편향(GP 편향)을 완화하고, 개인화된 추천을 더욱 강화하기 위한 것입니다.

프록시 변수(Proxy Variable)

정의

프록시 변수는 반사실적 추론에서 사용되는 개념으로, 직접적으로 관찰하기 어려운 변수들의 영향을 추정하기 위해 도입되는 대체 변수입니다. 이 변수는 주요 변수들의 영향을 결합하여 단일 지표로 표현합니다.

논문에서의 역할

논문에서는 GP와 PP의 영향을 동시에 고려하기 위해 프록시 변수 X를 도입했습니다. 이 프록시 변수는 GP와 PP를 결합하여 하나의 변수로 표현하며, 이 변수의 효과를 추정하여 추천 점수에 미치는 영향을 분석합니다. 이 접근 방식은 복잡한 인과 그래프에서 다양한 경로를 통해 발생하는 영향을 더 쉽게 다룰 수 있도록 합니다.

영향 추정 과정

1. 사실적 세계에서의 인과 그래프: 먼저 GP와 PP가 추천 점수에 미치는 영향을 설명하는 인과 그래프를 구성합니다. 여기서 GP와 PP는 각각 추천 점수 S에 직접적인 영향을 미칠 수 있습니다.
2. 프록시 변수를 사용한 추정: GP와 PP의 복합적인 영향을 추정하기 위해 프록시 변수 X를 도입합니다. 이 변수는 GP와 PP의 결합된 효과를 나타내며, 이를 통해 X가 추천 점수SS에 미치는 영향을 분석합니다.
3. 반사실적 세계의 구성: 반사실적 세계에서는 특정 변수들을 고정된 값(레퍼런스 상태)으로 설정하여 다른 변수들의 효과를 분리합니다. 이 과정에서 U와 I (사용자와 항목)의 레퍼런스 상태를 설정하고, 이를 통해 GP와 PP의 직접적인 영향을 구분합니다.
4. 추정 공식: 반사실적 추론을 통해 얻어진 영향을 다음과 같은 수식으로 표현할 수 있습니다.

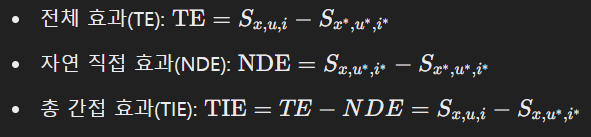
반사실적 추론을 통한 결과의 변화

반사실적 추론 기법을 사용하여 추천 점수에서 GP와 PP의 영향을 효과적으로 조정할 수 있습니다. 이로 인해:

• GP 편향 감소: GP에 의해 발생하는 편향을 줄이고, 다양한 항목이 추천될 수 있도록 합니다.
• PP 강화: PP의 영향을 강화하여 사용자별 맞춤형 추천을 개선할 수 있습니다.
• 정확도 향상: PPAC 프레임워크는 기존의 편향 감소 기법보다 높은 성능을 보였으며, 특히 회수율(Recall)과 NDCG에서 최대 46.8%와 61.9%의 향상을 달성했습니다.

연산 과정 요약

1. GP와 PP의 효과를 프록시 변수 X로 결합합니다.
2. 프록시 변수 X가 추천 점수 S에 미치는 직접적인 영향을 추정합니다.
3. 반사실적 세계에서의 추정을 통해 GP와 PP의 개별적 영향을 조정하고, 이를 바탕으로 추천 점수를 재계산합니다.
4. 조정된 추천 점수를 기반으로 최종 추천 리스트를 생성합니다.

이러한 방식으로 GP와 PP의 영향을 균형 있게 고려하여, 사용자에게 더 개인화되고 편향이 완화된 추천을 제공할 수 있습니다.

 

개인 인기(Personal Popularity, PP):
기존의 편향 감소(debiasing) 방법들은 항목의 글로벌 인기(GP)를 활용하지만, GP가 '글로벌' 관점에서 정의된다는 사실을 간과하고 있습니다. 즉, GP는 모든 사용자에게 동일한 인기 항목 세트(즉, GP 값이 가장 큰 항목들)를 사용합니다. 이는 특정 사용자에게 흥미롭지 않은 항목이 높은 GP 때문에 여전히 추천될 수 있음을 의미하며, 이는 사용자 경험과 추천 정확도에 해를 끼칠 수 있습니다. 게다가, 서로 다른 사용자들이 동일한 인기 항목 세트를 공유하기 때문에, 이로 인해 사용자는 동질적인 추천을 받을 수 있으며, 이는 GP 편향을 초래합니다. GP 문제를 해결하기 위해, 우리는 항목 인기를 사용자 인식(user-aware) 버전으로 변환한 '개인 인기(PP)'를 제안합니다. 특히, 각 사용자 𝑢에 대해 PP는 𝑢와 유사한 사용자들 사이에서의 항목 인기를 측정하며, 두 사용자가 과거 상호작용한 항목 세트에 큰 겹침이 있을 경우 이들이 유사하다고 말할 수 있습니다. GP와 비교할 때, PP는 개별 사용자의 선호를 고려하며, 각 사용자에 대해 별도의 인기 항목 세트를 식별할 수 있습니다. 2장에서, 우리는 MovieLens-1M 데이터셋을 사용하여 PP의 이점을 예시로 보여줍니다. 한편으로, PP 값이 높은 항목은 사용자들로부터 더 높은 평가를 받는 경향이 있어 PP가 유용하며 추천 과정을 개선하는 데 도움이 될 수 있음을 시사합니다. 다른 한편으로, 개인적으로 인기 있는 항목은 글로벌하게 인기 있는 항목과 다르며, 따라서 PP를 사용하면 글로벌 인기 항목 세트 외의 항목을 추천하고 GP 편향을 줄이는 데 도움이 될 수 있습니다.

PPAC 프레임워크: PP를 추천에 활용하기 위해, 우리는 개인 인식 반사실적(PPAC) 프레임워크를 제안합니다. 이 프레임워크의 설계 목표는 (i) 기존 추천 방법의 GP 편향을 줄이고, (ii) 모델에 종속되지 않으며, 다양한 기본 모델(e.g., MF 및 LightGCN)을 쉽게 지원할 수 있어야 한다는 것입니다. 우리의 PPAC와 기존 방법들 간의 차이를 설명하기 위해, 이를 그림 2에서 "인과 그래프"로 표현했습니다. 인과 그래프는 변수들을 나타내는 노드와, 한 변수가 다른 변수에 영향을 미치는 것을 나타내는 방향성 있는 비순환 그래프(DAG)입니다. 대부분의 추천 모델(e.g., MF 및 LightGCN)은 그림 2(a)에 있는 인과 그래프를 기반으로 설계되었으며, 이는 추천을 위해 사용자 및 항목 표현만을 활용합니다. 최근에는 그림 2(b)에 따라 GP를 통합한 편향 감소 방법들이 개발되었습니다. 그러나 우리는 그림 2(c)가 실제 점수 생성 과정을 더 정확하게 모델링한다고 주장합니다. 구체적으로, PP와 GP는 모두 경로 𝑃𝑃 → 𝑆 및 𝐺𝑃 → 𝑆를 통해 예측 점수에 직접적인 영향을 미칠 수 있습니다. 이는 사용자가 전반적인 트렌드나 친구들 간의 공유로 인해 글로벌 인기 항목과 개인적으로 인기 있는 항목을 모두 알 가능성이 더 높기 때문입니다. 그림 2(c)를 기반으로, 우리는 PP와 GP의 영향을 모두 고려하는 PPAC 프레임워크를 제안합니다. GP 편향을 완화하기 위해, PPAC 프레임워크는 그림 2(d)의 빨간 점선으로 나타난 바와 같이, 예측 점수에 대한 GP와 PP의 직접적인 영향을 추정하고 조정합니다. 이 두 경로의 영향을 추정하는 것이 어려우므로, PPAC는 반사실적 추론 기법을 사용하여 PP와 GP를 결합하는 프록시 변수를 도입합니다. 특히, 반사실적 추론은 일부 변수를 기준값에 할당한 가상의 세계를 상상하고, 이러한 변수들이 목표 변수에 어떻게 영향을 미치는지 추정합니다.

우리는 3가지 기본 모델과 3가지 데이터셋에서 10개의 기본 방법과 PPAC를 비교했습니다. 그 결과, PPAC는 모든 최신 편향 감소 방법들을 일관되게 능가했으며, 가장 잘 수행된 기본 방법보다 회수율(Recall)과 NDCG에서 각각 최대 46.8%와 61.9%의 개선을 보였습니다. 또한 실험 결과는 PPAC가 글로벌 인기 항목의 추천 빈도를 효과적으로 줄이고(즉, GP 편향을 완화하고), PP가 추천에 유익함을 시사했습니다.

요약하면, 우리는 다음과 같은 기여를 합니다:

• 기존 GP가 개별 사용자를 고려하지 못하는 문제를 해결하기 위해, 우리는 개별 사용자의 관심사를 포착하는 새로운 항목 인기 정의인 PP를 제안합니다.
• 추천 편향 감소를 위해 PP와 GP를 함께 고려하기 위해, 우리는 반사실적 추론 기법을 사용하여 모델에 종속되지 않는 PPAC 프레임워크를 설계했습니다.
• 우리는 PPAC와 우리의 설계를 평가하고, 최신의 편향 감소 방법들과 비교하는 실험을 수행했습니다.

 

2. 개인 인기(Personal Popularity)

우리는 전통적인 추천 설정을 고려합니다. 주어진 사용자 집합 U, 항목 집합 I, 그리고 사용자가 항목과 상호작용한 기록(예: 클릭, 구매)을 나타내는 사용자-항목 쌍 집합 R이 있을 때, 목표는 사용자가 항목 i∈I와 상호작용할 가능성을 예측하는 것입니다. 추천 모델은 일반적으로 점수 함수 f(u,i):U×I→R을 학습하며, 여기서 높은 점수는 상호작용할 가능성이 더 높음을 타냅니다. f(u,i)에 기반하여, 항목들은 점수에 따라 내림차순으로 정렬되고, 상위 항목들이 사용자 u에게 추천됩니다. 개인 인기(PP)를 정의하기 전에, 기존 연구에서 사용된 글로벌 인기(GP)를 다시 설명하겠습니다.

정의 1 (글로벌 인기): 특정 항목 i에 대해, 글로벌 인기(GP)는

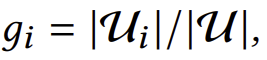
​로 표기되며, 여기서 Ui는 이전에 i와 상호작용한 사용자들의 집합입니다.

글로벌 인기는 사용자 집합 U 내에서 항목의 매력도를 측정합니다. 앞서 논의했듯이, GP는 개별 사용자의 개인적인 관심사를 반영하지 못하여 동질적인 추천과 GP 편향을 초래할 수 있습니다. 이 문제를 해결하기 위해, 우리는 사용자 관심사를 반영한 PP를 제안합니다.

PP를 계산하기 위해, 먼저 사용자 유사성을 정의합니다.

정의 2 (사용자 유사성): 사용자 u와 v가 주어졌을 때, 사용자 유사성은

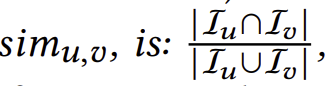
로 표기되며, 여기서 Iu와 Iv는 각각 사용자 u와 v가 상호작용한 항목들의 집합입니다.

우리의 사용자 유사성은 기본적으로 자카드 유사성(Jaccard Similarity)을 기반으로 하며, 두 집합 간의 겹침 정도를 측정합니다. 두 사용자가 상호작용한 항목들이 많이 겹칠수록 이들이 유사하다고 간주합니다.

정의 3 (유사 사용자 집합): 사용자 u에 대해, 유사 사용자 집합 Su​는 u와 가장 높은 사용자 유사성을 가진 k명의 사용자 집합으로 표기됩니다. 유사 사용자는 v∈Su로 표기됩니다. k는 하이퍼파라미터로 설정됩니다.

정의 4 (개인 인기): 사용자 u와 항목 i가 주어졌을 때, 개인 인기(PP)는

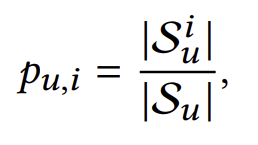
로 표기되며, 여기서 Sui는 Su​ 내에서 항목 i와 상호작용한 사용자들을 나타냅니다.
Sui⊆Su​이므로 pu,i는 [0, 1]의 값을 가집니다. 개념적으로, pu,i는 u와 유사한 관심사를 가진 사용자 그룹 내에서 항목 i의 매력도를 측정합니다. 따라서 pu,i는 개별 사용자의 개인적인 관심사를 반영하며, 서로 다른 사용자가 각기 다른 인기 항목 세트를 가질 수 있게 합니다.

우리의 PP 정의는 기본 협업 필터링 설정을 고려하며, 이는 사용자/항목 ID와 그들의 상호작용 기록만을 제공합니다. 이러한 데이터는 모든 추천 시스템에서 요구되며, 따라서 우리의 방법은 기존의 어떤 추천 모델에도 적용될 수 있습니다. PP 정의는 상호작용 타임스탬프, 사용자 프로필, 항목 설명 등 추가 정보가 제공될 때 확장될 수 있습니다. 예를 들어, 사용자 프로필(예: 나이, 성별, 지리적 위치)을 통해 보다 정확한 사용자 유사성을 정의하고, 따라서 PP를 더 정확하게 계산할 수 있습니다.

또한, 우리는 현재의 PP 정의가 비교적 단순하다고 하더라도, 각 사용자를 위한 별도의 인기 항목 세트를 사용하여 사용자 관심사를 포착하는 PP의 아이디어는 일반화될 수 있다고 주장합니다. 대안적인 PP 정의도 가능하며, 예를 들어 사용자와 항목 간의 다중 홉 연결성을 고려할 수 있습니다. 우리는 보다 정교한 PP 정의에 대한 연구를 미래 작업으로 남겨둡니다.

PP 분석: 항목 i가 주어졌을 때, GP 값 gi​는 모든 사용자에게 동일하지만(정의 1), PP 값 pu,i는 사용자에 따라 다릅니다(정의 4). 두 사용자가 동일한 유사 사용자 집합 Su​를 가질 가능성은 낮으므로, 사용자들 간에 PP 값이 다를 가능성이 큽니다. 게다가, PP는 개별 사용자의 관심사를 반영하여 추천을 보다 개인화하고 글로벌 인기 항목의 추천을 줄일 수 있습니다.

우리는 MovieLens-1M 데이터셋을 사용하여 PP를 분석했으며, 이 데이터셋은 영화에 대한 사용자 평점(1-5점)을 포함하고 있습니다. 표 1은 이 데이터셋의 세부 정보를 제공합니다. 우리는 모든 항목을 평균 PP 값에 따라 정렬하고, 이를 다섯 개의 동일한 크기의 그룹으로 나눈 후, 각 그룹의 항목에 대한 평균 사용자 평점을 계산했습니다. 그림 3(a)는 PP 값이 높은 항목이 사용자들로부터 더 높은 평점을 받는 경향이 있음을 보여주며, 이는 PP가 추천에 유용할 수 있음을 시사합니다. 우리는 또한 개인적으로 인기 있는 항목이 글로벌하게도 인기 있는지 여부를 조사했습니다. 우리는 50개의 가장 높은 GP 값을 가진 항목 집합 IGP를 추출했습니다. 각 사용자 u에 대해, 우리는 50개의 가장 높은 PP 값을 가진 항목 집합 IPP,u를 추출했습니다. 그런 다음, du=∣IPP,u−IGP∣를 계산했으며, 이는 50개의 가장 높은 PP 값을 가진 항목들 중 상위 50개의 GP 값 항목에 속하지 않는 항목의 수를 나타냅니다. 그림 3(b)는 du 값에 따라 사용자를 그룹화한 결과를 보여줍니다. 우리는 (1) du​가 10 미만인 사용자가 없음을 관찰했고, (2) du>20인 사용자가 약 85%임을 확인했습니다. 이는 PP가 GP로는 충분히 반영되지 않는 사용자별 선호도를 포착하고 있음을 시사합니다.

3. PPAC 프레임워크

이 절에서는 먼저 반사실적 추론(counterfactual inference)의 주요 개념을 소개하고(3.1절), 인과적 관점에서 편향을 줄이기 위한 PPAC 프레임워크를 제시합니다(3.2절). 다음으로, PPAC 프레임워크를 모델 설계에 적용하고(3.3절), 모델 학습 및 추론 절차를 논의합니다(3.4절).

3.1 반사실적 추론을 위한 기초

PPAC 프레임워크에 대한 배경 지식을 제공하기 위해, 우리는 반사실적 추론의 기본 개념을 소개합니다 [43, 53, 55]. 추가 세부 사항은 [37]에서 확인할 수 있습니다.

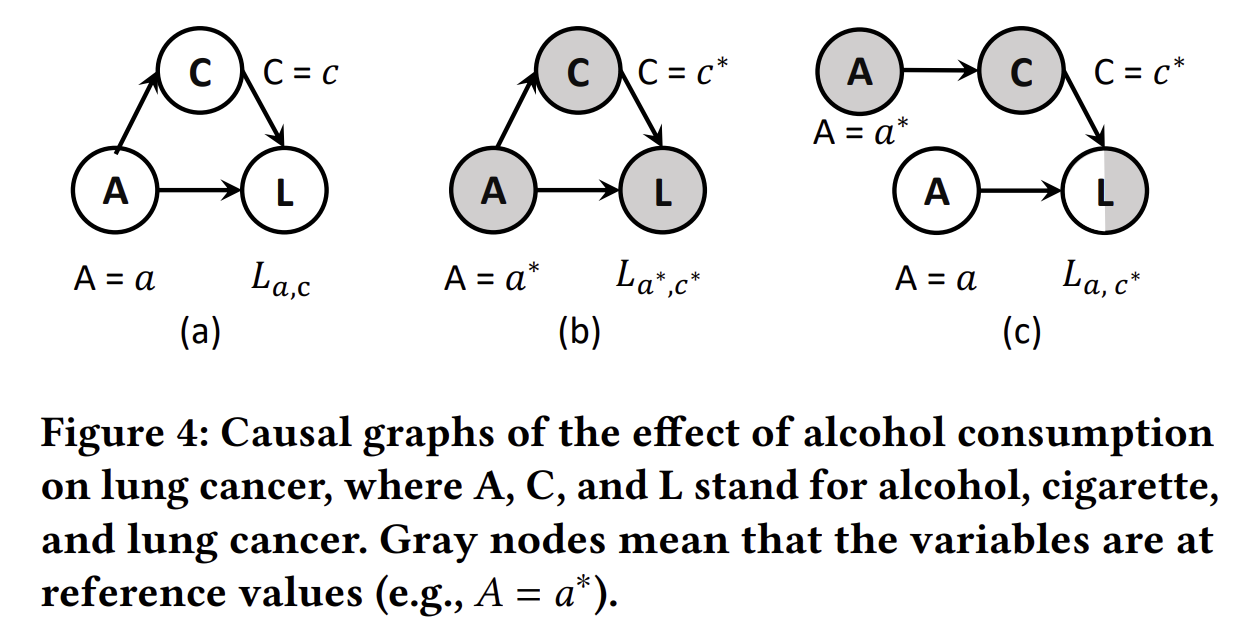
인과 그래프(Causal Graph): 인과 그래프는 방향성 비순환 그래프(DAG)로, 노드는 확률 변수를 나타내고, 엣지는 변수들 간의 인과 관계를 나타냅니다. 그림 4(a)는 인과 그래프의 예시를 보여줍니다. 여기서 대문자(예: 𝐴)는 확률 변수를 나타내고, 소문자(예: 𝑎)는 해당 변수의 관찰된 값을 나타냅니다. 𝐴 → 𝐿은 알코올 소비(𝐴)가 폐암(𝐿)에 직접적인 영향을 미친다는 것을 의미합니다. 𝐴 → 𝐶 → 𝐿은 𝐴가 𝐶(담배 소비)를 통해 𝐿에 간접적으로 영향을 미친다는 것을 의미하며, 𝐶는 매개 변수로 작용합니다 [53]. 𝐿의 값은 조상 노드들의 값에서 계산될 수 있으며, 다음과 같이 공식화할 수 있습니다:

L𝑎,𝑐=L(𝐴=𝑎,𝐶=𝑐),     𝑐 = 𝐶_{𝑎} = 𝐶(𝐴 = 𝑎)

여기서 𝐿(·)과 𝐶(·)는 각각 𝐿과 𝐶의 구조적 방정식입니다. 𝐶𝑎는 한 사람이 알코올 소비량 𝑎를 가정할 때의 담배 소비량을 나타냅니다. 𝐿𝑎,𝑐는 해당 사람이 알코올 소비량 𝑎와 담배 소비량 𝑐를 가졌을 때의 폐암 결과를 나타냅니다. 𝐴가 𝐿에 미치는 직접적 영향과 간접적 영향을 각각 계산하기 위해서는 반사실적 추론을 사용해야 합니다.

반사실적 추론(Counterfactual Inference): 반사실적 추론은 본질적으로 특정 변수의 값을 변경했을 때 결과가 어떻게 달라지는지를 상상하는 사고 활동입니다 [22]. 예를 들어 그림 4(b)에서는 "알코올 소비량이 다른 값으로 설정되었다면 어떻게 되었을까?"를 고려합니다. 회색 노드는 변수들이 기준 상태(즉, 예를 들어 𝐴 = 𝑎와 같은 기준값에 할당된 상태)에 있다는 것을 의미하며, 이는 사실과 독립적으로 개입되어 인과 효과를 추정하는 데 사용됩니다 [54]. 그림 4(c)는 반사실적 세계의 인과 그래프를 보여줍니다. 여기서 𝐶는 𝑐 = 𝐶(𝐴 = 𝑎*)로 설정되고, 𝐿은 𝐿𝑎,𝑐* = 𝐿(𝐴 = 𝑎,𝐶 = 𝑐*)로 설정됩니다. 이는 𝐴가 𝐿에 미치는 영향을 연구하기 위해 만들어진 상상의 시나리오일 뿐입니다. 이것을 반사실적 시나리오라고 하는 이유는, 현실에서는 발생하지 않겠지만 𝐴 = 𝑎와 𝐴 = 𝑎*를 동시에 설정하여 사실과 가정을 결합하고 있기 때문입니다 [43].

인과 효과(Causal Effect): 𝐴가 𝐿에 미치는 인과 효과는 조상 노드 𝐴가 한 단위 변화했을 때 목표 변수 𝐿의 값이 얼마나 변하는지를 나타냅니다 [49]. 예를 들어 그림 4에서, 𝐴 = 𝑎가 𝐿에 미치는 총 효과(TE)는 다음과 같이 정의됩니다:

𝑇𝐸=𝐿𝑎,𝑐−𝐿𝑎∗,𝑐∗​

TE는 자연 직접 효과(NDE, 즉 𝐴 → 𝐿 경로를 통한 효과)와 총 간접 효과(TIE, 즉 𝐴 → 𝐶 → 𝐿 경로를 통한 효과)의 합으로 분해될 수 있으며, 이는 다음과 같이 계산할 수 있습니다:

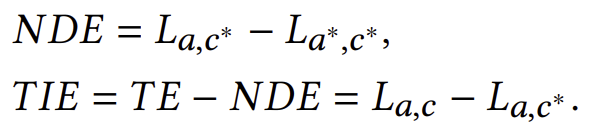
3.2 반사실적 편향 감소 추천

이 절에서는 먼저 GP와 PP가 인과 그래프를 통해 예측 점수에 어떻게 영향을 미치는지 논의하고, 그 다음으로 PPAC 프레임워크가 편향을 줄이기 위한 논리를 소개합니다.

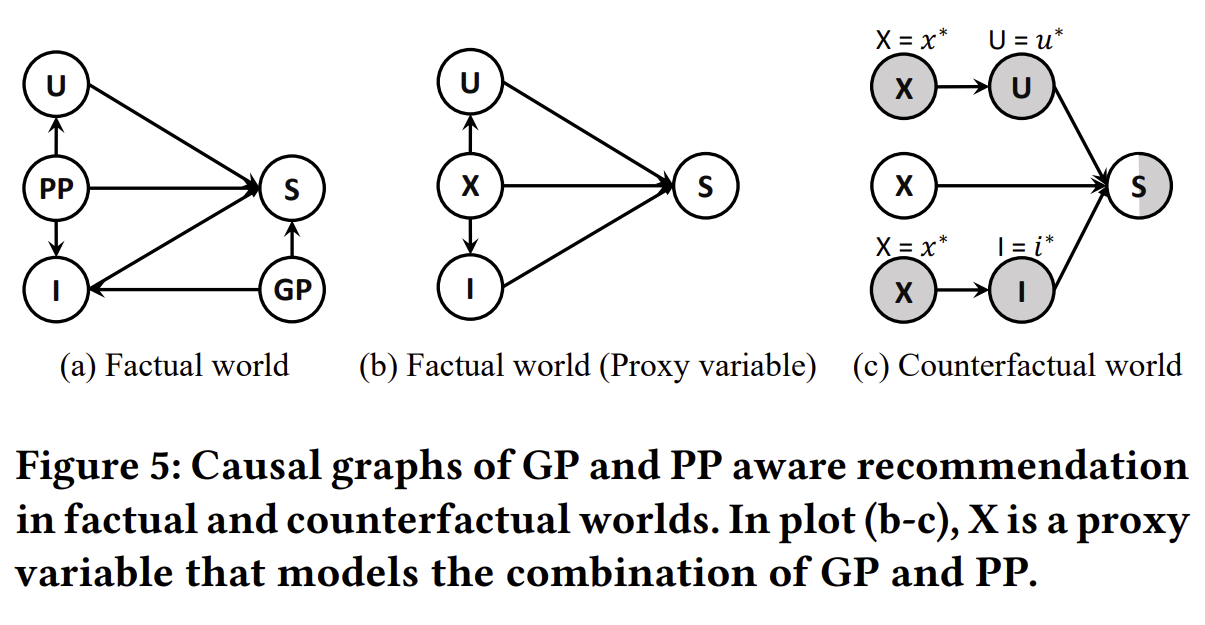
그림 5(a)에서 우리는 사실적 세계의 추천을 인과 그래프로 추상화하였으며, 여기서 𝑈, 𝐼, 𝑃𝑃, 𝐺𝑃, 𝑆는 각각 사용자 표현, 항목 표현, 개인 인기, 글로벌 인기, 사용자-항목 예측 점수를 나타냅니다. 예측 점수 𝑆는 사용자-항목 상호작용의 가능성을 모델링합니다. 인과 관계의 관점에서 보면, GP와 PP 모두 항목들이 높은 GP 및 PP 값을 가지면 사용자가 이들을 더 잘 알게 되고, 따라서 추천될 가능성이 높아지기 때문에 𝑃𝑃 → 𝑆 및 𝐺𝑃 → 𝑆 경로를 통해 예측 점수에 직접적으로 영향을 미칠 수 있습니다. 우리는 이 두 경로의 직접적인 효과를 조정하는 것이 편향을 줄이는 효과적인 방법이라고 주장하는데, 이는 더 유연한 추천을 가능하게 하기 때문입니다.

그러나 𝑃𝑃 → 𝑆 및 𝐺𝑃 → 𝑆의 직접적인 효과를 별도로 추정하는 것은 매우 어려우며, 대부분의 기존 연구들은 하나의 직접적인 효과 경로만을 다룹니다 [43, 49, 54]. 우리는 근접 인과 추론(proximal causal inference) [53, 59]에서 영감을 받아 그림 5(b)에 새로운 변수 𝑋를 도입했으며, 이는 단일 처리 체제에서 다양한 혼란 변수를 통합하는 프록시 변수입니다. 특히, 우리는 PP와 GP를 결합하여 𝑆에 미치는 인과 효과를 계산하기 위해 단일 노드 𝑋를 사용합니다. PP는 𝑈와 𝐼 모두에 영향을 미칠 수 있기 때문에, 프록시 변수 𝑋도 𝑈와 𝐼 모두에 영향을 미칠 수 있어야 합니다.

이제 문제는 𝑋가 𝑆에 미치는 직접적인 효과를 어떻게 추정할 것인가로 귀결됩니다. 3.1절에서 소개된 인과 효과 계산에 따라, 먼저 그림 5(c)에 반사실적 세계를 구성합니다. 방정식 (3)에 따라, 𝑋의 총 효과(TE)는 다음과 같이 작성될 수 있습니다:

𝑇𝐸=𝑆𝑥,𝑢,𝑖−𝑆𝑥∗,𝑢∗,𝑖∗​

간접 경로(즉, 𝑋 → 𝑈 → 𝑆 및 𝑋 → 𝐼 → 𝑆)는 𝑈와 𝐼를 기준 상태로 설정함으로써 차단되며, 즉 𝐼 = 𝑖* = 𝐼(𝑋 = 𝑥*) 및 𝑈 = 𝑢* = 𝑈(𝑋 = 𝑥*)으로 설정됩니다. 그 후, 우리는 𝑋의 자연 직접 효과(NDE)를 다음과 같이 계산할 수 있습니다:

𝑁𝐷𝐸=𝑆𝑥,𝑢∗,𝑖∗−𝑆𝑥∗,𝑢∗,𝑖∗​

방정식 (4)에 따라, 총 간접 효과(TIE)는 다음과 같이 계산됩니다:

𝑇𝐼𝐸=𝑇𝐸−𝑁𝐷𝐸=𝑆𝑥,𝑢,𝑖−𝑆𝑥,𝑢∗,𝑖∗​

우리의 목표는 추천에서 𝑋 → 𝑆(즉, NDE)의 직접적인 효과를 제어하여 GP 편향을 완화하는 것입니다. 따라서, 우리는 반사실적 추론을 통해 다음과 같이 편향이 제거된 예측을 얻습니다:

​

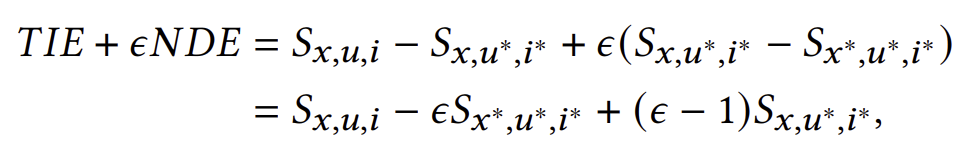
여기서 𝜖는 NDE의 가중치를 제어하는 하이퍼파라미터입니다. 𝑥*, 𝑢* 및 𝑖*는 인과 효과를 계산하는 데 사용되는 기준값으로, 3.1절에서 논의했듯이 특정 물리적 의미를 가지지 않을 수 있습니다.

누군가는 GP 편향을 줄이기 위해 직관적으로 GP 효과를 줄이고 PP 효과를 확대해야 한다고 주장할 수 있습니다. 그러나 우리는 프록시 변수를 사용하여 GP와 PP를 결합함으로써 NDE를 추정합니다. 중요한 점은, 프록시 변수는 오직 NDE를 추정하는 데 도움을 주기 위해 사용된다는 것입니다. 실제로 모델을 사용하여 NDE를 조정할 때는 GP와 PP 효과를 별도로 수정하게 됩니다. 이는 다음 절에서 자세히 설명할 것입니다.

3.3 모델 설계

이 절에서는 3.2절에서 논의된 반사실적 편향 감소 추천을 모델 설계를 통해 어떻게 구현하는지 소개합니다. 방정식 (8)에 따라, 우리는 𝑆𝑥,𝑢,𝑖, 𝜖𝑆𝑥*,𝑢*,𝑖* 및 (𝜖 − 1)𝑆𝑥,𝑢*,𝑖*을 추정해야 합니다.

𝑆𝑥,𝑢,𝑖 추정: 기존의 추천 모델들은 예측 점수를 추정하기 위해 사용자와 항목 표현에만 의존하는 반면, 우리는 𝑋의 중요성을 명시적으로 고려합니다. 𝑆𝑥,𝑢,𝑖를 추정하기 위해, 우리는 추정된 𝑋 값(𝑥ˆ𝑢,𝑖로 표기)을 기존 추천 모델의 예측 점수 𝑓𝑅과 곱합니다. 이 𝑓𝑅은 편향이 제거되어야 하는 기본 모델로 다음과 같이 정의됩니다:

𝑆𝑥,𝑢,𝑖=𝑥ˆ𝑢,𝑖∗𝑓𝑅(𝑈=𝑢,𝐼=𝑖)

여기서 𝑓𝑅은 편향이 제거되어야 하는 기존의 어떤 추천 모델도 될 수 있습니다. 𝑋는 GP와 PP를 결합한 것이므로, 우리는 𝑥ˆ𝑢,𝑖 = 𝜎(𝑓𝑃𝑃 (𝑈 = 𝑢, 𝐼 = 𝑖)) ∗ 𝜎(𝑓𝐺𝑃 (𝐼 = 𝑖))로 구현합니다. 여기서 𝜎는 시그모이드 함수이고, 𝜎(𝑓𝑃𝑃 (·))와 𝜎(𝑓𝐺𝑃 (·))는 각각 PP와 GP의 추정 모델입니다. 𝑓𝑃𝑃와 𝑓𝐺𝑃는 간단하게 다층 퍼셉트론(MLP)으로 구현되었지만, 다른 신경망으로 대체할 수 있습니다. GP는 항목에 특정된 특성이고 PP는 사용자와 항목 모두의 특성이므로, 𝑓𝐺𝑃는 항목만 입력으로 받는 반면, 𝑓𝑃𝑃는 사용자와 항목 모두를 입력으로 받습니다. 시그모이드 함수는 추정된 GP와 PP 값이 (0, 1) 범위 내에 있도록 하여, 다른 모델을 무효화하지 않도록 합니다.

𝜖𝑆𝑥,𝑢,𝑖* 추정: 이 맥락에서 모든 변수는 기준 상태로 간주되며, 이는 그림 5(b)에서 모든 경로의 인과 효과가 고정됨을 의미합니다. 따라서 𝑆𝑥*,𝑢*,𝑖는 관련된 특정 사용자와 항목에 관계없이 일정한 값을 나타냅니다. 𝜖의 값에 관계없이, 𝜖𝑆𝑥,𝑢*,𝑖*는 모든 사용자-항목 예측에서 일관성을 유지하므로, 이 항목을 추가해도 사용자에 대한 항목 순위에는 영향을 미치지 않으며, 이를 직접 무시할 수 있습니다.

(𝜖 − 1)𝑆𝑥,𝑢,𝑖 추정: 여기서 𝑢와 𝑖는 기준 상태로, 𝑆는 𝑋 → 𝑈 → 𝑆 및 𝑋 → 𝐼 → 𝑆 경로에 의해 영향을 받지 않습니다. 3.1절에서 설명했듯이, 𝑋 = 𝑥와 𝑋 = 𝑥*는 반사실적 세계에서 공존할 수 있습니다. 우리의 맥락에서 우리는 𝑆𝑥,𝑢*,𝑖* = 𝑥ˆ𝑢,𝑖 ∗ 𝑓𝑅 (𝑈 = 𝑢*, 𝐼 = 𝑖*)로 추정하며, 여기서 𝑓𝑅 (𝑈 = 𝑢*, 𝐼 = 𝑖*)는 𝑈 → 𝑆 및 𝐼 → 𝑆의 영향을 차단하는 고정된 상수값이며, 𝑥ˆ𝑢,𝑖의 값은 여전히 특정 사용자와 항목에 따라 달라집니다. 다음으로, 우리는 𝜏 = (𝜖 − 1)𝑓𝑅 (𝑈 = 𝑢*, 𝐼 = 𝑖*)로 설정하며, 이는 𝑥ˆ𝑢,𝑖에 대한 조정 가능한 가중치로 작용하여 𝑋(즉, GP와 PP의 결합)의 영향을 조정할 수 있도록 합니다. 더 나은 조정을 위해, 우리는 다음과 같이 구현합니다:

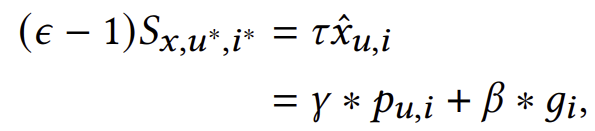
여기서 𝛾와 𝛽는 각각 PP와 GP에 대한 조정 가능한 가중치입니다. 𝑔𝑖는 훈련 세트에서 계산된 항목 𝑖의 관측된 GP이고, 𝑝𝑢,𝑖는 훈련 세트에서 평가된 사용자 𝑢와 항목 𝑖에 대한 관측된 PP입니다. (𝜖 − 1)𝑆𝑥,𝑢*,𝑖* 추정에서는 관측된 GP와 PP 값을 사용하고, 𝑆𝑥,𝑢,𝑖 추정에서는 모델이 예측한 값을 사용한다는 점에 유의하세요. 이는 사용자와 항목 표현이 기준 상태에 있을 때 예측 점수에 직접적인 영향을 미칠 수 없기 때문입니다. 그럼에도 불구하고, 𝑓𝐺𝑃와 𝑓𝑃𝑃는 사용자와 항목 표현을 입력으로 사용하며, 이들의 매개변수는 훈련 과정에서 지속적으로 변화합니다. 결과적으로, 우리는 (𝜖 − 1)𝑆𝑥,𝑢*,𝑖* 추정 시 예측 값을 고정된 관측 값으로 대체합니다. 4.3절의 실험은 이러한 설계의 효과를 보여줍니다.

3.4 학습과 추론

다음으로, 모델 학습과 추론에 대한 절차를 소개합니다. 그림 6은 이러한 과정의 개요를 제공합니다.

학습: 앞서 설명한 추정 과정을 바탕으로, 우리는 𝑓𝑅, 𝑓𝑃𝑃, 𝑓𝐺𝑃를 학습해야 합니다.
𝑓𝑅을 학습하기 위해, 모델 예측이 추천을 수행하기보다는 훈련 세트의 분포와 일치하도록 하는 것이 학습의 목표임을 주목하세요. 따라서, 우리는 학습과 추론 단계에서 사용자-항목 상호작용 확률을 추정하는 데 다른 방법을 사용합니다. 구체적으로, 훈련 세트는 인과 그래프를 통해 사실적 세계에서 생성되었으며(그림 5(a)), 여기서는 모든 인과 효과가 조정되지 않았습니다. 따라서, 사용자 𝑢와 항목 𝑖의 과거 훈련 세트에서의 상호작용 확률 𝑦ˆ𝑢,𝑖를 추정하기 위해, 우리는 그림 5(a)에서 모든 경로가 제한되지 않고 예측 점수에 영향을 미칠 수 있다는 가정에 따라 예측 점수 𝑆𝑥,𝑢,𝑖의 추정 절차를 따릅니다. 즉,

(11)

여기서 𝑟ˆ𝑢,𝑖는 기본 모델의 예측을 나타냅니다. 𝜎(𝑝ˆ𝑢,𝑖) = 𝜎(𝑓𝑃𝑃 (𝑈 = 𝑢, 𝐼 = 𝑖))와 𝜎(𝑔ˆ𝑖) = 𝜎(𝑓𝐺𝑃 (𝐼 = 𝑖))는 각각 모델이 예측한 PP와 GP 값을 나타냅니다. 그런 다음, 우리는 추천에서 널리 사용되는 Bayesian Personalized Ranking (BPR) 손실 [20, 33, 39]을 적용하여 이를 학습합니다:

(12)

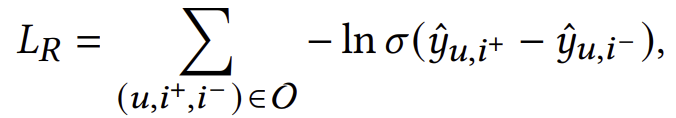
여기서 O = {(𝑢,𝑖+,𝑖−)| (𝑢,𝑖+) ∈ R, (𝑢,𝑖−) ∈ R−}는 훈련 세트를 나타내고, (𝑢,𝑖+,𝑖−)는 하나의 훈련 샘플입니다. R은 관측된 사용자-항목 상호작용의 집합이며, 𝑖+는 𝑢가 상호작용한 긍정적 샘플입니다. 집합 R−은 임의로 샘플링된 관측되지 않은 사용자-항목 쌍을 포함하며, 𝑖−는 𝑢가 이전에 상호작용하지 않은 임의로 샘플링된 부정적 샘플입니다.

𝑓𝑃𝑃와 𝑓𝐺𝑃(PP 및 GP 추정 모델)를 학습하기 위해, 우리는 이를 회귀 과제로 간주하고 관측된 값을 실제 값으로 사용한 다음, Mean Squared Error (MSE) 손실 [40, 50]을 적용합니다:

(13)

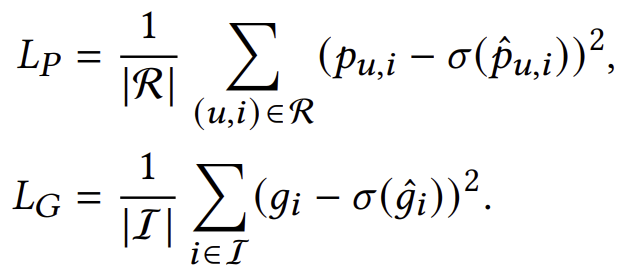
이 모든 것을 종합하여 최종 손실 함수는 다음과 같습니다:

(14)

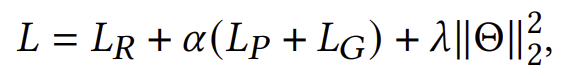
여기서 𝛼는 조정 가능한 하이퍼파라미터이며, Θ는 모델에서 학습 가능한 모든 파라미터를 나타내고, 𝜆는 𝐿2 정규화의 가중치입니다.

추론: 사실적 세계에서의 예측에 의존하는 대신, 우리는 NDE를 조정하고 3.2절에서 설명한 대로 방정식 (8)을 적용하여 추천을 만듭니다. 이전 추정값을 결합하여 다음과 같은 추론 공식을 얻습니다:

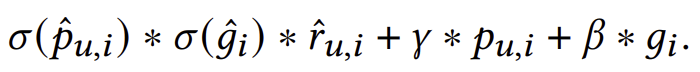
여기서 𝛾와 𝛽는 각각 PP와 GP에 대한 조정 가능한 가중치로 작용합니다. 우리는 또한 이 반사실적 추론을 직관적인 예를 통해 설명합니다. 모든 사용자들 사이에서 동등하게 인기 있는 두 항목 𝑖와 𝑗(즉, 𝑔𝑖 = 𝑔𝑗)가 있지만, 𝑖가 사용자 𝑢와 유사한 관심사를 공유하는 사용자들 사이에서는 𝑗보다 더 인기가 많다고 가정합니다(즉, 𝑝𝑢,𝑖 > 𝑝𝑢,𝑗). 만약 방정식 (11)이 𝑦ˆ𝑢,𝑖 < 𝑦ˆ𝑢,𝑗로 순위 점수를 추정한다면, 𝑗가 𝑖보다 더 높은 순위에 위치하게 됩니다. 반사실적 추론을 통해, 우리는 𝛾 ∗ 𝑝𝑢,𝑖 항목을 조정하여, 𝑖가 𝑗보다 앞서게 되는 더 정확한 순위를 얻을 수 있습니다. 우리의 실험에서는 𝛾의 양의 값과 𝛽의 음의 값이 GP 편향을 완화하는 데 효과적임을 관찰했습니다. 이러한 값들은 PP 효과를 증폭시키고 GP 효과를 감소시켜, 추천 모델이 GP 편향에 더 잘 대처하고 사용자 관심사를 보다 정확하게 예측할 수 있도록 합니다.

 

4. 실험 평가

이 절에서는 PPAC 프레임워크를 평가하기 위한 광범위한 실험을 수행하여 다음 연구 질문들에 답하고자 합니다:

• RQ1: PPAC가 최신 편향 감소 방법들을 능가할 수 있는가?
• RQ2: PPAC의 주요 설계가 정확도에 어떤 영향을 미치는가?
• RQ3: PPAC가 글로벌 인기 편향을 성공적으로 완화하는가?
• RQ4: 하이퍼파라미터가 PPAC에 어떤 영향을 미치는가? (부록 참조)

4.1 실험 설정

데이터셋: 우리는 세 가지 공개된 데이터셋(MovieLens-1M, Gowalla, Yelp2018)에서 실험을 수행했으며, 그 통계는 표 1에 보고되었습니다.

기본 모델: 우리는 MF 기반 모델(BPRMF), 신경망 기반 모델(NCF), 그래프 기반 모델(LightGCN)과 같은 세 가지 대표 모델을 실험했습니다.

기준 방법: 포괄적인 비교를 위해, 우리는 10개의 기준 방법을 사용했습니다. 여기에는 기본 모델(Base model), 2개의 순위 기반 방법(MostPop, MostPPop), 그리고 7개의 최신 편향 감소 방법이 포함됩니다. 이 방법들은 2개의 역확률점수(IPS) 기반 방법(IPS, IPS-C), 2개의 정규화 기반 방법(LapDQ, INRS), 3개의 인과 그래프 기반 방법(DICE, PDA, MACR)입니다.

• MostPop은 모든 항목을 GP로 직접 순위 매기고 상위 항목을 추천합니다. 이 방법은 편향 감소를 고려하지 않으며, 참조 결과를 제공하기 위해 사용됩니다.
• MostPPop은 각 사용자에게 상위 PP 항목을 직접 추천합니다. 이 방법은 PP의 효과를 보여주기 위해 설계되었습니다.

평가 방법: 기존의 임의로 하위 데이터셋을 선택하여 테스트하는 평가 전략은 사용자의 실제 선호도 분포를 반영할 수 없습니다. 따라서, 우리는 기존 방법들을 따라 개입된 테스트 세트에서 실험을 수행했습니다. 구체적으로, 모든 항목이 동일한 수의 상호작용을 받도록 보장하여 데이터셋에서 10%의 상호작용을 테스트 세트로 샘플링하고, 동일한 방식으로 10%를 검증 세트로 샘플링했습니다. 나머지 상호작용은 훈련에 사용됩니다. 이렇게 함으로써 GP 편향의 영향을 제거한 반사실적 환경을 만들어 사용자 선호도를 더 잘 반영할 수 있습니다. 우리는 모든 순위 프로토콜을 채택하고, 두 가지 일반적으로 사용되는 지표인 Recall과 NDCG를 보고합니다. 여기서 지표는 상위 50개의 결과를 기준으로 계산됩니다.

구현 세부 사항: 우리는 모든 모델을 PyTorch를 사용하여 구현하고, 사용자와 항목 임베딩의 차원을 64로 설정했습니다. 우리는 그리드 탐색을 통해 모든 하이퍼파라미터를 조정하여 최상의 결과를 얻습니다. 구체적으로, 그래프 기반 모델의 경우 그래프 합성 계층 수를 3으로 설정했습니다. 학습률은 0.01이고, 모든 실험에서 학습 배치 크기는 8092입니다. 기본적으로 PPAC에서 PP 계수 𝛾는 256이고, GP 계수 𝛽는 -128입니다. 회귀 손실 가중치 𝛼는 0.1이고, L2 정규화 계수 𝜆는 1e-4입니다. PP 계산을 위해 고려해야 할 유사 사용자 수(𝑘)는 30입니다.

4.2 주요 결과 (RQ1)

표 2는 PPAC가 다양한 기본 모델에 대해 Recall@50 및 NDCG@50 측면에서 다양한 기준 방법과 비교한 성능을 보여줍니다. 주요 관찰은 다음과 같습니다.

• PPAC는 다양한 지표, 데이터셋 및 기본 모델에서 모든 기준 방법을 일관되게 능가했습니다. PPAC가 기존의 가장 잘 수행된 편향 감소 방법보다 Recall과 NDCG 측면에서 각각 최대 46.8%와 61.9%의 개선을 이루었으며, 이는 PPAC가 다양한 기본 모델과 데이터셋에서 효과적임을 입증합니다.
• 제안된 MostPPop은 BPRMF가 기본 모델일 때 보통 두 번째로 높은 순위를 차지하며, 이는 PP가 추천에 매우 강력하고 효과적임을 시사합니다. 또한, MostPPop(즉, 더 높은 PP 항목을 추천)은 모든 경우에 MostPop(즉, 더 높은 GP 항목을 추천)을 크게 능가하며, PP가 GP보다 더 강력함을 보여줍니다.
• PPAC의 개선은 보통 BPRMF와 NCF에서 LightGCN보다 더 두드러집니다. 이는 LightGCN이 기본 모델 중에서 가장 높은 정확도를 달성했기 때문에 개선의 여지가 적기 때문입니다. 다양한 데이터셋을 고려했을 때, PPAC의 개선은 MovieLens-1M보다 Gowalla와 Yelp2018에서 더 적습니다. 이는 MovieLens-1M이 상호작용이 적어 모델 학습이 더 쉬웠기 때문입니다.

4.3 구성 요소 분석 (RQ2)

다른 구성 요소의 효과: PPAC의 설계를 더 깊이 이해하기 위해 특정 구성 요소를 비활성화한 상태에서 구성 요소 분석을 수행했습니다. 구체적으로, 세 가지 변형을 개발했습니다.

• w/o CI는 반사실적 추론을 비활성화하고 사실적 세계의 예측을 사용하여 추천합니다.
• w/o PP는 PP 추정 모델(𝑓𝑃𝑃)과 학습 및 추론 중 PP와 관련된 모든 항목을 제거합니다.
• w/o GP는 GP 추정 모델(𝑓𝐺𝑃)과 학습 및 추론 중 GP와 관련된 모든 항목을 제거합니다.

이러한 변형들을 기본 모델과 PPAC와 비교했습니다. 표 3에 보고된 결과에서 몇 가지 관찰을 할 수 있습니다. (1) PPAC는 모든 변형보다 일관되게 더 나은 성능을 보이며, 우리의 모든 추정 및 설계가 편향 감소에 있어서 올바르고 효과적임을 나타냅니다. (2) w/o CI는 모든 경우에서 기본 모델을 능가하며, 반사실적 추론이 추천에서 PP와 GP의 직접적인 효과를 효과적으로 제어할 수 있음을 강조합니다. (3) w/o PP는 일반적으로 w/o GP와 비교했을 때 성능이 더 나쁘며, 이는 PP가 GP보다 편향 감소에 더 강력하다는 것을 나타내며, PP를 제거하면 성능이 크게 떨어집니다.

관측된 인기와 예측된 인기의 효과: 3.3절에서 설명한 대로, 우리는 𝑆𝑥,𝑢,𝑖와 (𝜖 − 1)𝑆𝑥,𝑢*,𝑖* 추정에서 PP와 GP의 예측값을 사용하고, (𝜖 − 1)𝑆𝑥,𝑢*,𝑖*에서 관측값을 사용했습니다. 이 설계의 효과를 보여주기 위해 실험을 수행했습니다. 구체적으로, 모델이 예측한 인기(𝜎(𝑝ˆ𝑢,𝑖)와 𝜎(𝑔ˆ𝑖)) 또는 관측된 인기(𝑝𝑢,𝑖와 𝑔𝑖)를 두 가지 추정에서 모두 사용하여 성능을 비교하고, 훈련 및 추론 단계를 수정했습니다. 공간 제약으로 인해 Gowalla 데이터셋에서만 결과를 보고합니다. PPAC-Pred는 모델이 예측한 GP 및 PP 값을 사용한 경우를 나타내며, PPAC-Obs는 관측된 값만 사용한 경우를 나타냅니다.

결과에서 우리는 PPAC가 모든 경우에서 두 변형보다 더 나은 성능을 보이며, 우리의 추정 절차가 올바르고 효과적임을 나타냅니다. 직관적으로, 관측된 인기가 더 정확하므로 인기 효과를 미세 조정하는 데 더 적합한 반면, 예측된 인기는 더 나은 사용자/항목 임베딩을 학습하는 데 중요한 역할을 하여 더 정확한 예측을 제공합니다.

4.4 편향 감소 분석 (RQ3)

PPAC의 편향 감소 능력을 이해하기 위해, 우리는 항목들이 훈련 세트에서 받은 상호작용 수를 기준으로 항목들을 그룹으로 나누고, 그림 7은 각 항목 그룹에 대한 평균 추천 빈도와 정확도(즉, recall)를 보고합니다. 파란색 막대는 각 항목 그룹에서의 항목 비율을 나타내며, 선은 다른 기준 방법들의 빈도 또는 recall의 추세를 보여줍니다. 공간 제한으로 인해 Gowalla 데이터셋에서만 결과를 제시합니다. 다른 데이터셋에서도 유사한 관찰이 있음을 참고하세요. 우리는 비교를 위해 기존의 기준 방법들 중에서 일반적으로 두 번째로 높은 순위를 차지하는 MACR을 포함시켰습니다. 결과에서 다음과 같은 관찰을 할 수 있습니다.

• PPAC는 기본 모델과 MACR에 비해 가장 글로벌하게 인기 있는 항목 그룹에서의 추천 빈도가 감소했음을 보여줍니다. 이는 PPAC가 GP 편향의 영향을 완화하는 데 더 효과적임을 시사합니다. 또한, 그림 7(c-d)는 PPAC가 모든 항목 그룹에서 가장 높은 recall을 달성하여 다른 기준 방법들보다 사용자들의 실제 선호도에 더 잘 맞는 추천을 하고 더 정확한 추천을 제공함을 보여줍니다.
• 글로벌하게 가장 인기 없는 항목 그룹(0-10 상호작용을 가진 항목들)은 recall에서 가장 큰 증가를 경험하고 더 많은 추천을 받습니다. 이는 전통적인 추천 모델이 GP 편향에 취약하고 이미 글로벌하게 인기 있는 항목을 더 많이 추천하는 경향이 있음을 암시합니다. 그러나 PPAC는 GP가 높은 항목을 기반으로만 추천하는 것을 효과적으로 피하고 대신 관련 사용자에게 항목을 추천하여 롱테일 항목의 추천을 강화합니다.

5. 관련 연구

추천 시스템에서의 인기 편향. 추천 시스템의 피드백 루프(즉, 노출이 상호작용에 영향을 미침)로 인해 편향이 증폭되고 점점 심각해질 수 있습니다. 몇 가지 방법들이 GP 편향을 완화하기 위해 제안되었으며, 이는 사용자의 탐색을 방해하고 사용자를 동질화로 이끄는 것으로 입증되었습니다. 이러한 방법들은 세 가지 범주로 분류할 수 있습니다. (1) 역확률점수(IPS) 기반 방법: IPS는 항목의 GP의 역수를 사용하여 각 상호작용 기록에 가중치를 부여하여 글로벌하게 인기 있는 항목의 상호작용이 훈련에 미치는 영향을 줄입니다. IPS-CN은 IPS-C에 가중치 정규화를 추가하지만, 추가적인 편향을 도입합니다. (2) 순위 조정 또는 정규화: LapDQ는 예측된 추천 목록에서 항목을 재순위 매겨 정확도와 글로벌하게 인기 없는 항목 커버리지 간의 균형을 맞춥니다. ESAM은 글로벌하게 인기 있는 항목에서 학습된 지식을 글로벌하게 인기 없는 항목으로 이전하여 충분한 상호작용이 없는 글로벌하게 인기 없는 항목 문제를 해결합니다. r-Adj는 그래프 신경망 기반 모델의 이웃 집계 과정에서 정규화 강도를 제어합니다. (3) 인과 방법: PDA는 인과 그래프 모델을 채택하고 GP를 고려하여 순위 점수를 계산합니다. DICE는 사용자 임베딩을 사용자 관심사와 순응성을 나타내는 두 개의 차원으로 분리하여 사용자 순응성의 영향을 받지 않고 사용자 관심사를 학습합니다. MACR은 멀티태스크 학습을 통해 사용자 관심사, 사용자 순응성 및 GP를 추정합니다. 이 모든 방법은 GP(즉, 모든 사용자에게 하나의 인기 항목 세트를 사용)를 채택하므로 개별 사용자의 관심사를 모델링하지 못합니다. 반면에 우리의 PP는 각 사용자를 위한 별도의 인기 항목 세트를 사용하여 개별 관심사를 모델링하므로 GP 편향을 자연스럽게 완화하고 더 나은 추천을 제공합니다.

인과 추천: 인과 추론 기법은 컴퓨터 비전, 자연어 처리, 정보 검색 등 다양한 분야에서 응용되고 있습니다. 추천 시스템에서 인과 추론은 사용자 행동의 내재된 인과 메커니즘을 이해하는 데 도움이 될 수 있습니다. 예를 들어, CR은 노출 효과에 개입하여 클릭베이트 문제를 해결합니다. COR은 사용자 특성 변화와 분포 외 추천 문제를 제어하여 해결합니다. HCR은 사용자 피드백과 항목 특성의 인과 효과를 분해하기 위해 전방문 조정 방법을 채택합니다. MCMO는 추천을 다중 원인 다중 결과 추론 문제로 모델링하여 노출 편향을 처리합니다. 우리는 GP 편향에 중점을 두고, PP와 GP를 결합한 인과 그래프를 개발하여 추천 모델을 개선했습니다.

6. 결론

이 논문은 각 사용자의 개별 관심사를 고려하여 서로 다른 인기 항목 세트를 찾는 개인 인기(PP)의 새로운 개념을 제안합니다. 기존의 글로벌 인기(GP)는 모든 사용자에게 하나의 인기 항목 세트만을 찾습니다. 따라서, PP는 GP 편향을 자연스럽게 완화하고 더 나은 추천을 수행할 수 있습니다. 또한, 우리는 PP와 GP를 결합하고 반사실적 추론 기법을 사용하여 추천에 대한 이들의 직접적인 영향을 제어하여 편향을 제거하는 개인 인기 인식 반사실적(PPAC) 프레임워크를 제안합니다. 광범위한 실험 결과, PPAC가 기존의 추천 편향 감소 방법들을 크게 능가함을 보여줍니다.

 

이런 @ 하고 뒤에 나오는 숫자들은 뭐야?

"@ 뒤에 나오는 숫자"는 주로 평가 지표에서 특정 조건을 나타내기 위해 사용됩니다. 이 경우, 예를 들어 "Recall@50" 또는 "NDCG@50" 같은 표현에서 '@' 뒤에 오는 숫자는 추천 시스템의 평가에서 상위 몇 개의 결과를 고려하는지를 나타냅니다.

• Recall@50: 이 지표는 추천 시스템이 상위 50개의 추천 항목 중에서 실제로 사용자가 상호작용한 항목을 얼마나 많이 맞추었는지를 측정합니다. 즉, 상위 50개의 추천 결과 내에서 사용자에게 유용한 결과를 얼마나 잘 제공했는지를 평가하는 것입니다.
• NDCG@50 (Normalized Discounted Cumulative Gain): 이 지표 역시 상위 50개의 추천 항목에 대한 평가를 의미합니다. NDCG는 추천된 항목의 순위와 관련된 점수를 평가하는 방법으로, 더 높은 순위에 있는 추천 항목이 더 유용한 경우 높은 점수를 받습니다. 여기서 '@50'은 상위 50개의 추천 항목을 기준으로 계산되었음을 의미합니다.

따라서, "@" 뒤에 오는 숫자는 추천 시스템의 성능 평가에서 특정 개수의 상위 항목을 기준으로 한 평가를 나타내는 것입니다.