모두를 위한 머신러닝 - 14주차 퀴즈

아래 문장에 있는 빈칸에 들어갈 가장 적당한 단어를 하나 고르시오.

“이상 데이터 검출 모델은 (________)를 사용하여 데이터가 정상인지, 비정상인지 여부를 결정하며, 만약 데이터의 확률이 정해진 (________)보다 작으면 이상 데이터로 판정한다.”

하나를 선택하세요.

확률분포함수, 최소값

확률분포함수, 임계값

예측함수, 최소값

예측함수, 임계값

가우시안 분포! -> 확률 분포 함수, 입실론 == threshold == 임계값

문장의 빈칸에 들어갈 가장 적절한 단어는 "확률분포함수, 임계값"입니다. 따라서 정답은 2번입니다.

문장 완성:

“이상 데이터 검출 모델은 (확률분포함수)를 사용하여 데이터가 정상인지, 비정상인지 여부를 결정하며, 만약 데이터의 확률이 정해진 (임계값)보다 작으면 이상 데이터로 판정한다.”

선택지 분석:

1. 확률분포함수, 최소값:
   • 확률분포함수를 사용하는 것은 맞지만, 최소값은 문맥에 맞지 않습니다. 일반적으로 이상 데이터 검출에서는 임계값을 사용합니다.
2. 확률분포함수, 임계값:
   • 확률분포함수를 사용하여 데이터의 정상 여부를 판단하고, 이 확률이 정해진 임계값보다 작으면 이상 데이터로 판정하는 것이 일반적인 방법입니다. 문맥에 잘 맞습니다.
3. 예측함수, 최소값:
   • 예측함수는 데이터의 정상 여부를 결정하는 데 적절하지 않습니다. 또한, 최소값은 임계값을 의미하지 않으므로 문맥에 맞지 않습니다.
4. 예측함수, 임계값:
   • 예측함수는 확률분포함수에 비해 덜 일반적인 용어입니다. 이상 데이터 검출에서는 확률분포함수가 더 적절한 용어입니다. 임계값은 적절하지만, 예측함수와 함께 사용하기에는 부적절합니다.

이유:

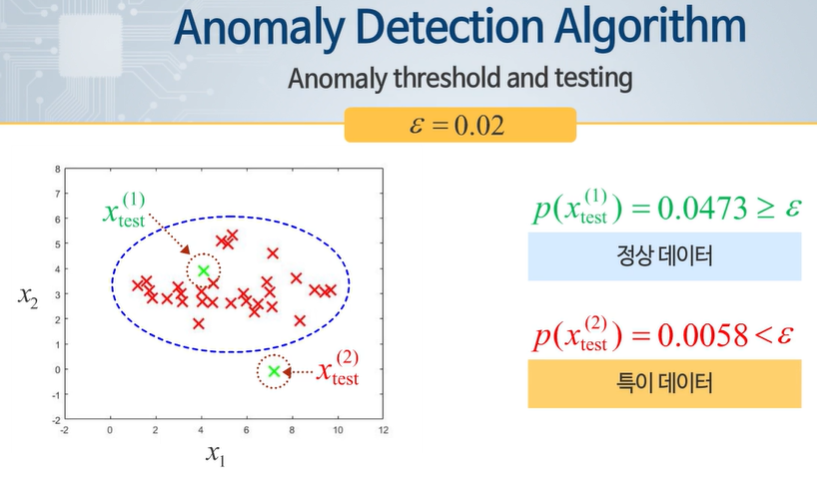
이상 데이터 검출(anomaly detection)에서 자주 사용하는 방법은 데이터의 확률분포를 분석하고, 특정 데이터 포인트의 확률이 임계값(threshold)보다 작으면 그 데이터를 이상치로 판정하는 것입니다. 따라서 "확률분포함수"와 "임계값"이 문맥에 가장 잘 맞습니다.

1 : Fraud detection은 이상데이터 검출(anomaly detection)의 한 예에 해당됨.

2 : 이상데이터 검출 모델에서는 가우시안 확률분포 함수를 사용하여 대상 데이터가 정상범위에 속해 있는지, 비정상 범위에 속해 있는지 여부를 결정함.

3 : 데이터의 확률값이 미리 정해진 임계값(threshold) 보다 작으면 이상데이터로 간주함.

정답 : 확률분포함수, 임계값

 

 

다변수 가우시안 분포에 대한 다음 설명 중 올바른 것을 모두 고르시오.

하나 이상을 선택하세요.

서로 다른 특징값 간의 상관 관계를 자동으로 획득한다

계산량이 비교적 적다

공분산 행렬과 그 역행렬을 계산해야 할 필요가 있다

학습 데이터의 수가 특징 값의 수보다 적어야 한다.

2, 4는 무조건 틀린거고, 1번이 애매한데...   맞지 않을까 싶습니다. 내가 넣어주는게 아닌데 계산하면서 자동으로 나오는 거니까.

다변수 가우시안 분포에 대한 설명 중 올바른 것을 모두 고르시오:

1. 서로 다른 특징값 간의 상관 관계를 자동으로 획득한다
   • 올바른 설명입니다. 다변수 가우시안 분포는 공분산 행렬을 통해 서로 다른 특징값 간의 상관 관계를 나타낼 수 있습니다. 이 공분산 행렬은 각 특징값 쌍 간의 상관 관계를 자동으로 반영합니다.
2. 계산량이 비교적 적다
   • 잘못된 설명입니다. 다변수 가우시안 분포를 사용하려면 공분산 행렬과 그 역행렬을 계산해야 하기 때문에 계산량이 비교적 많습니다. 특히 특징값의 수가 많을수록 계산량이 기하급수적으로 증가합니다.
3. 공분산 행렬과 그 역행렬을 계산해야 할 필요가 있다
   • 올바른 설명입니다. 다변수 가우시안 분포에서는 공분산 행렬과 그 역행렬을 사용하여 확률 밀도 함수를 계산하므로, 이를 계산해야 할 필요가 있습니다.
4. 학습 데이터의 수가 특징 값의 수보다 적어야 한다.
   • 잘못된 설명입니다. 학습 데이터의 수는 일반적으로 특징값의 수보다 많아야 합니다. 그렇지 않으면 공분산 행렬이 특이 행렬이 되어 역행렬을 계산할 수 없게 되거나, 계산이 매우 불안정해질 수 있습니다.

따라서 올바른 설명은 첫 번째와 세 번째입니다.

다변수 가우시안 분포는 여러 특징값 들 간의 상관 관계를 자동적으로 획득함

다변수 가우시안 분포는 각 특징값들이 서로 독립적이라는 가정에 비해 계산량이 더 많음

다변수 가우시안 분포를 이용하면, 공분산 행렬과 그 역행렬을 계산하여야 함

 

The correct answers are: 서로 다른 특징값 간의 상관 관계를 자동으로 획득한다, 공분산 행렬과 그 역행렬을 계산해야 할 필요가 있다