인공지능 - 인간의 지능을 모방하여 사람이 하는 일을 기계가 할 수 있도록 하는 기술
머신러닝 - 데이터의 특징을 스스로 판별하지 못한다.
딥러닝 - 데이터의 특징을 스스로 분석하여 답을 찾는다. 비정형 데이터 전부 가능
feature extraction 피쳐 추출- 데이터 별로 어떤 특징을 가지고 있는지 찾아내고, 그것을 토대로 데이터를 벡터로 변환하는 작업
데이터셋 - train + validation(검증 용이므로 데이터가 충분치 않다면 사용 X) + test
배치 크기 * iteration/epoch = 데이터 셋 크기
지도 학습 - 정답을 주고, 오차를 통해 학습
비지도 학습 - 정답 없이 비슷한 데이터를 클러스트링(범주화)하여 예측하는 방법
강화 학습 - 경험을 토대로 보상을 극대화 한다.
transfer learning 전이학습 - 사전에 학습이 완료된 모델(pre- tranined model)을 가지고 원하는 학습에 미세 조정 기법(fine tuning)을 이용하여 학습시키는 방법
사전 학습 모델 - 풀고자 하는 문제와 비슷하면서 많은 데이터로 이미 학습된 모델
단층 퍼셉트론에선 XOR 연산을 할 수 없다. -> 다층 퍼셉트론의 등장
AND (NAND(x1,x2), OR (x1,x2) ) 를 진행하면 XOR을 얻을 수 있다.
weight와 bias를 얻는 문제이다.
비선형성을 추가하기 위해 activation function을 추가한다.
sigmoid - 분류 문제를 확률적으로 표현하는데 사용 BUT vanishing gradient problem 문제가 발생
trah - 결과의 평균을 0으로 만드는데 성공했으나 기울기 소실 문제는 여전하다.
ReLU - 학습 속도가 빠르고, 기올기 소멸 문제가 발생하지 않는다. BUT 음수는 0으로 출력해서 학습 능력 감소


가중합 == 전달함수(transfer function) - activation에 전달해주기 때문에
손실함수 - 정답 값과 예측값의 오차를 구하는 방법
오차를 통해 weight를 업데이트 한다. - 역전파 backpropagation
은닉층 너무 많다 - overfitting
해결 - dropout, 데이터 셋 다양성 높이기, 복잡도 줄이기, regularization 적용하기, 조기 종료, 배치 정규화, 앙상블
딥러닝의 문제점
기울기 소멸 - ReLU
경사 하강법의 성능 저하 - 다양한 optimizer를 통해 한계 해결
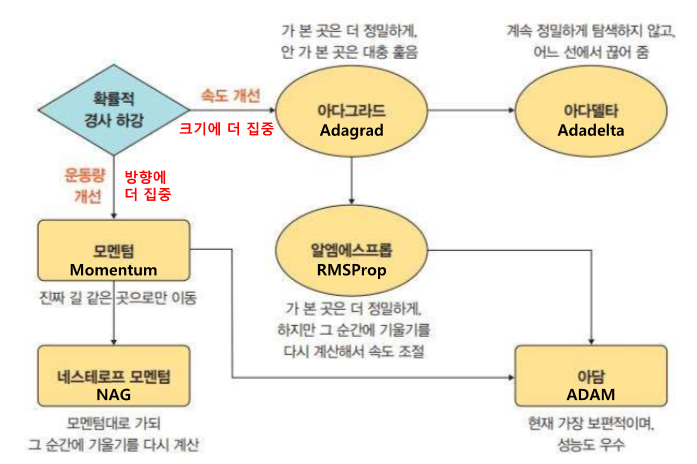
Adagrad - 학습률을 점차 줄여서 후반에 학습을 조금씩 한다.
Adadelta - Adagrad + 학습률이 0으로 가는 것을 막아 학습이 멈추는 문제를 해결
RMSProp - Adagrad + gamma = 학습률의 크기를 비율로 조정할 수 있다.
Momentum - 이전 방향을 누적해서 관성의 효과를 얻는다.
NAG - Momentum의 관성을 줄였다.
Adam - Momentum + RMSProp
weight 초기화가 0이면 - 전부 0이니까 늘 같은 값을 출력
상수 - 편향을 가지게 된다.
가우시안 분포를 따르면서 너무 작은 값 - 출력이 점점 0으로 변한다.
가우시안 분포를 다르면서 너무 큰 값 - 출력이 1 이나 -1로 모여버린다.
Xavier - Sigmoid = 입력 데이터와 가중치는 서로 독립이며 동일한 분포를 가지고 평균이 0이다.
Ge - ReLU =
regularization - 규제화, 정규화 = 최적해로 가는 길을 잘 찾게 해준다. 최적해를 잘 찾도록 정보를 추가하는 기법, 최적화 과정에서 성능을 개선할 수 있는 포괄적인 기법들을 포함한다.
1. 모델 단순화
2. 사전 지식을 표현하여 최적해를 빠르게 찾도록 함 - 가중치 감소 (가우시안 분포라면 제곱, 라플라스 분포라면 그냥)
3. 확률적 성질을 추가 - 데이터 증강, 잡음 주입, drop out
4. 여러 가설을 고려하여 예측 - 앙상블
배치 정규화 - layer를 지날 때 마다 data 분포가 왜곡된다 -> input의 분포를 이동시켜 해결한다.
왜곡되는 현상 - 내부 공변량 변화 = 뒤로갈 수록 큰 문제가 된다. -> 배치 정규화가 해결 -> gradient의 흐름이 원활해진다.
배치 정규화도 파라미터를 학습하여 손실함수를 최소화하는 방향으로 이동한다.
보통은 가중합 이후에 넣지만 활성함수 이후에 적용해도 성능이 좋다고 한다.
Dropout - 뉴런을 랜덤하게 잘라내서 새로운 모델을 생성하므로 배깅과 비슷하다.
모델 간의 독립성을 전제로 하는 배깅보다 좋은 성능을 가지긴 어렵지만 시간이 오래 걸리지 않아 실용적이다.
잡음 주입
입력 데이터 - 데이터 증강 = 아주 작은 분산을 갖는 잡음을 넣으면 가중치 감소와 동일한 정규화 효과
feature에 잡음 주입 - 데이터가 추상화된 상테에서 데이터를 증강하는 것 - 의미있는 단위로 데이터 증강이 일어나서 성능이 크게 향상된다.
모델 가중치에 잡음 주입 - Dropout = 최소 지점이 평지로 변화해서 새로운 데이터에 대한 일반화 성능이 향상된다.
label에 잡음 주입 - 소프트 레이블링 = 레이블에 오류가 있을 경우 이상하게 학습되는 것을 막기 위해 일정 만큼 확률을 다른 클래스에 배분한다.
'인공지능 > 공부' 카테고리의 다른 글
| 강화학습 퀴즈 - MDP, 벨만 방정식, 플래닝, 정책 평가, 정책 개선... with ChatGpt (0) | 2024.04.22 |
|---|---|
| 딥러닝개론 정리 2 - Convolution, CNN, 합성곱 (0) | 2024.04.22 |
| 강화 학습 중간 정리 4 - MC, 벨만 방정식, planning, 최적 정책 찾기, value 평가 (0) | 2024.04.22 |
| 딥러닝 개론 정리 7강 - 합성곱 신경망 2 CNN (0) | 2024.04.21 |
| 강화 학습 중간 정리 3 - MDP 모를 때 최적 정책 찾기 (0) | 2024.04.21 |