






이미지에서 설명하는 내용은 이항 분류(binomial classification) 문제에서의 클래스 결정 방식과 클래스 확률을 계산하는 과정을 나타냅니다. 주어진 입력 ( X )에 대해 두 클래스 ( Y_1 )과 ( Y_2 ) 중 어느 쪽에 속하는지 결정하는 과정이며, 확률적 관점에서 접근합니다.
확률 ( P(Y_1|X) )는 입력 ( X )가 주어졌을 때 클래스 ( Y_1 )에 속할 조건부 확률입니다. 이는 베이즈 정리를 사용하여 다음과 같이 계산할 수 있습니다:
[ P(Y_1|X) = \frac{P(X|Y_1)P(Y_1)}{P(X)} ]
여기서 ( P(X|Y_1) )은 클래스 ( Y_1 )이 주어졌을 때 입력 ( X )가 관측될 확률이고, ( P(Y_1) )은 클래스 ( Y_1 )의 사전 확률입니다. ( P(X) )는 모든 가능한 클래스에 대해 입력 ( X )가 관측될 확률을 나타내며, ( P(X) )는 ( P(X|Y_1)P(Y_1) )와 ( P(X|Y_2)P(Y_2) )의 합으로 계산할 수 있습니다.
이 과정에서 ( P(X) )는 클래스가 ( Y_1 )이거나 ( Y_2 )일 때 ( X )가 나타날 확률의 총 합으로, 양쪽의 확률을 모두 고려한 정규화 상수 역할을 합니다. 이를 통해 각 클래스에 속할 조건부 확률을 계산하게 되며, 이는 결국 로지스틱 회귀 모델에서 사용되는 시그모이드 함수와 동일한 형태로 나타납니다.
이미지에 표시된 부분은 이 과정에서 ( P(Y_1|X) )와 ( P(Y_2|X) )를 계산하는 과정입니다. 만약 ( P(Y_2|X) )가 ( P(Y_1|X) )보다 크면 ( X )는 클래스 ( Y_2 )로 분류됩니다. 반대로 ( P(Y_1|X) )가 ( P(Y_2|X) )보다 크거나 같으면 ( X )는 클래스 ( Y_1 )로 분류됩니다. 이를 통해 로지스틱 회귀 모델에서의 결정 경계가 어떻게 형성되는지를 수학적으로 설명하는 것입니다.
이미지에서 ( P(X) )가 "합의 일"로 표현된 것은, ( P(X) )가 두 클래스에 대한 ( P(X|Y_k)P(Y_k) ) (여기서 ( k )는 1 또는 2) 값들의 합으로 계산되는 정규화 상수임을 의미합니다. ( a_k = \ln(P(X|Y_k)P(Y_k)) )로 표시된 것은 로그 확률로, 지수화하고 정규화하여 시그모이드 함수를 통해 최종 확률을 구하는 형태로 변환하는 과정을 나타냅니다.










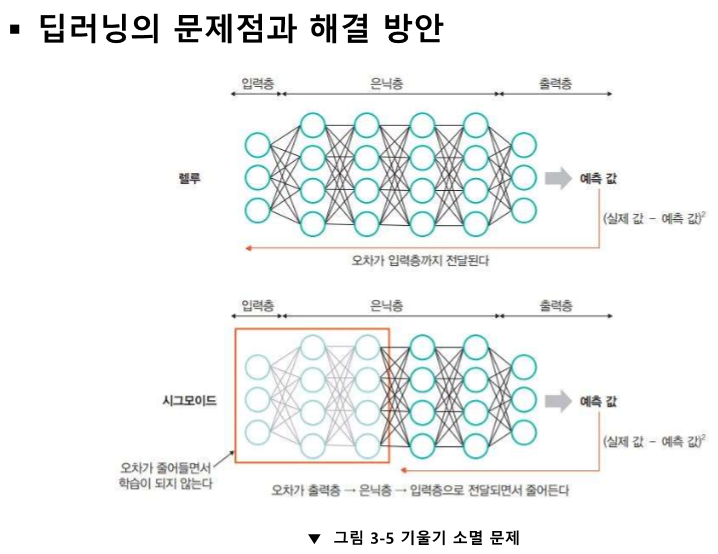
오차가 크다
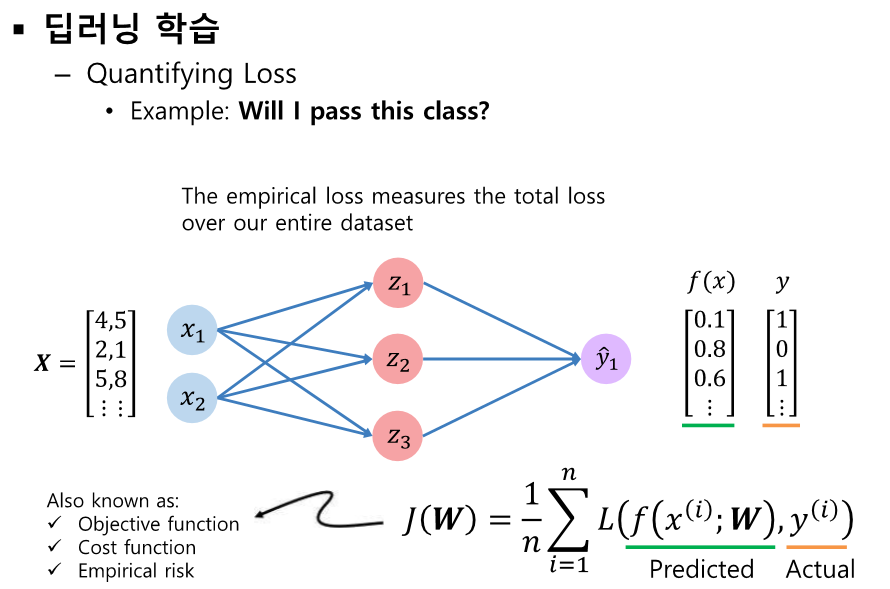
이제 cost function을 통해 파라미터 수정하러 가보자





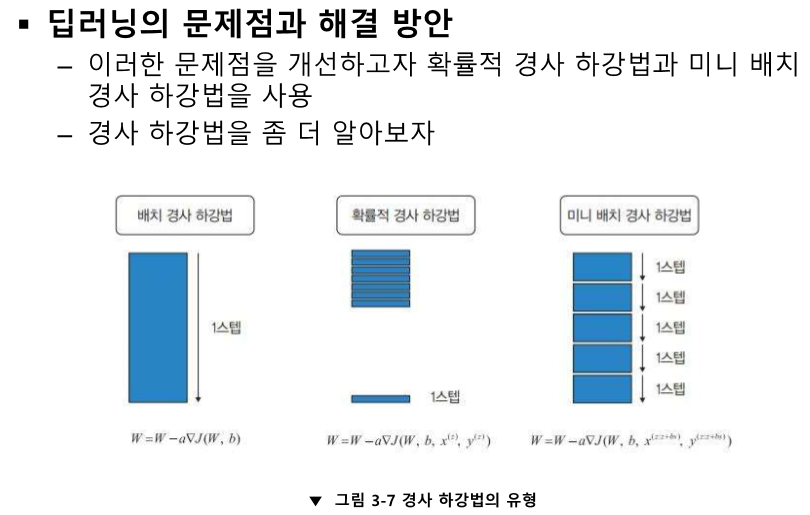
기울기의 반대로 지속해서 나간다.



기울기의 반대 방향으로 진행한다.








딥러닝과 비선형 활성 함수를 사용함으로써 복잡한 문제를 해결할 수 있다.

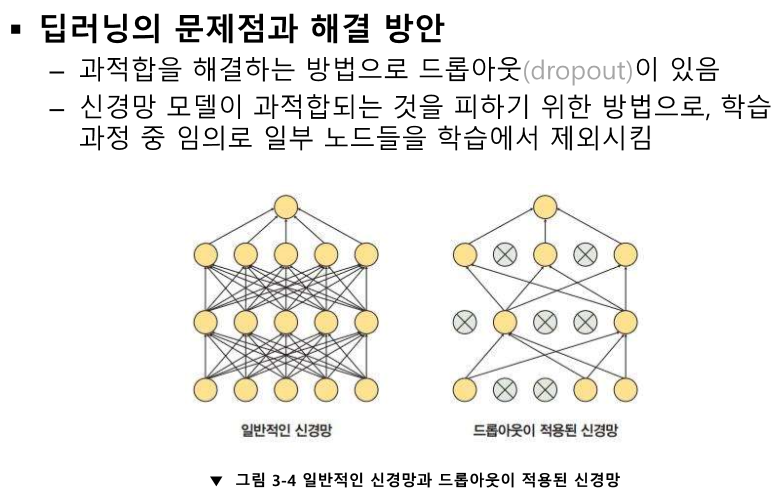
overfitting이 나오겠네요










'인공지능 > 공부' 카테고리의 다른 글
| 딥러닝 개론 5강 - 초기화와 정규화 (0) | 2024.04.16 |
|---|---|
| 딥러닝 개론 4강 - 최적화 (0) | 2024.04.16 |
| 딥러닝 개론 2강 - 순방향 신경망 forword propagation (0) | 2024.04.16 |
| 딥러닝 개론 1강 - 딥러닝 개요 (0) | 2024.04.16 |
| 생성형 인공지능 입문 7주차 퀴즈 (1) | 2024.04.16 |