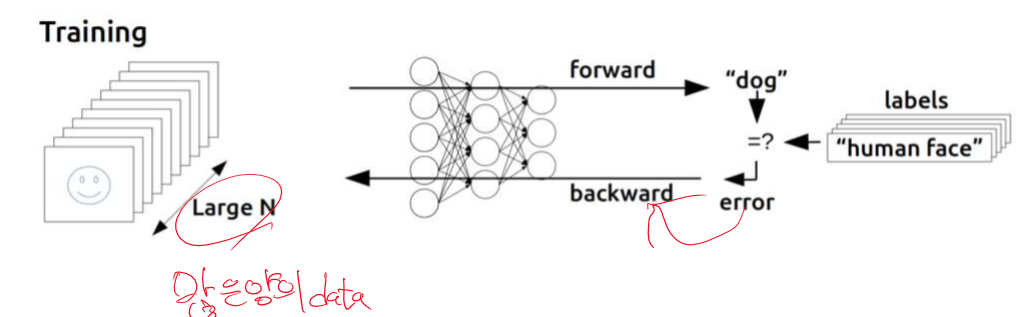
Evaluation - Forward propagation == inference 추정하다.
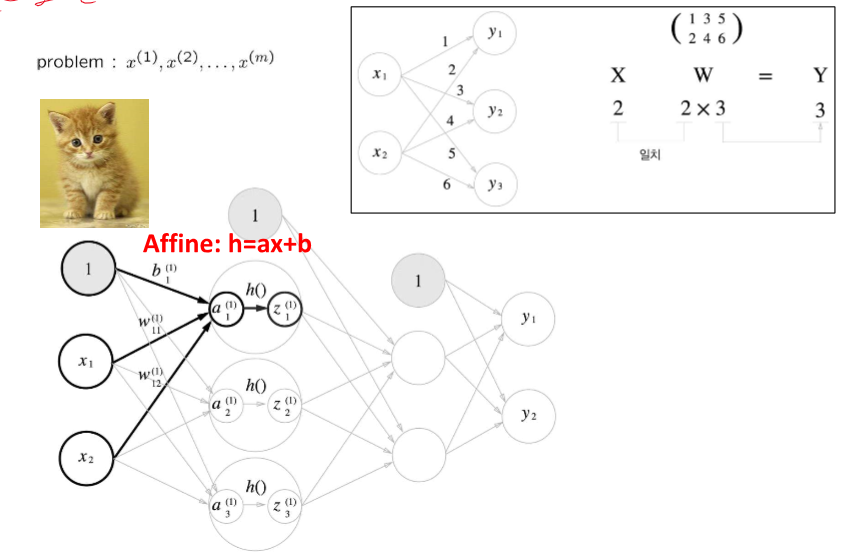
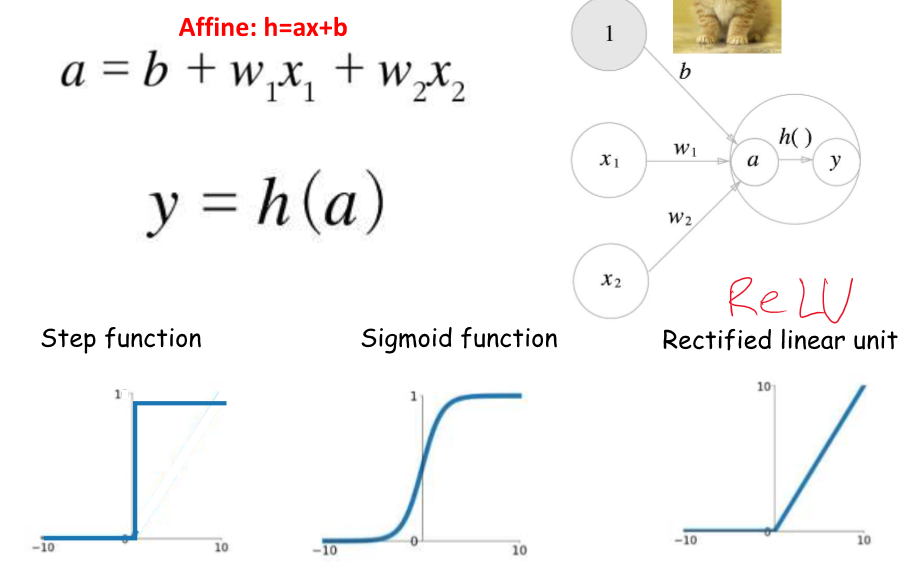

exp 사용하는 이유는 최대값에 민감하게 반응하기 때문이ㅏㄷ

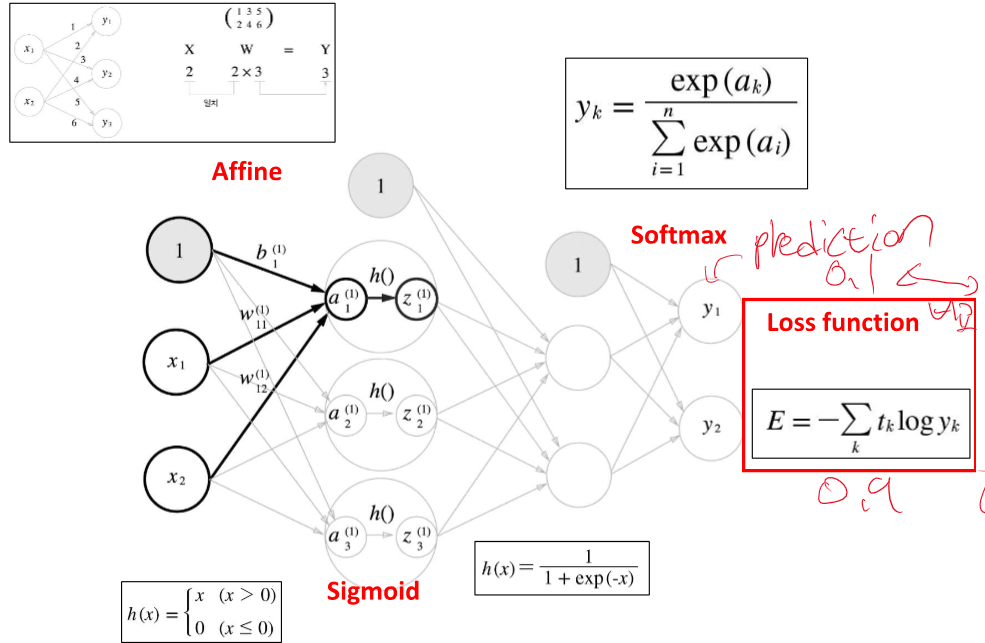
loss = prediction과 label을 비교하여 차이를 구한다.
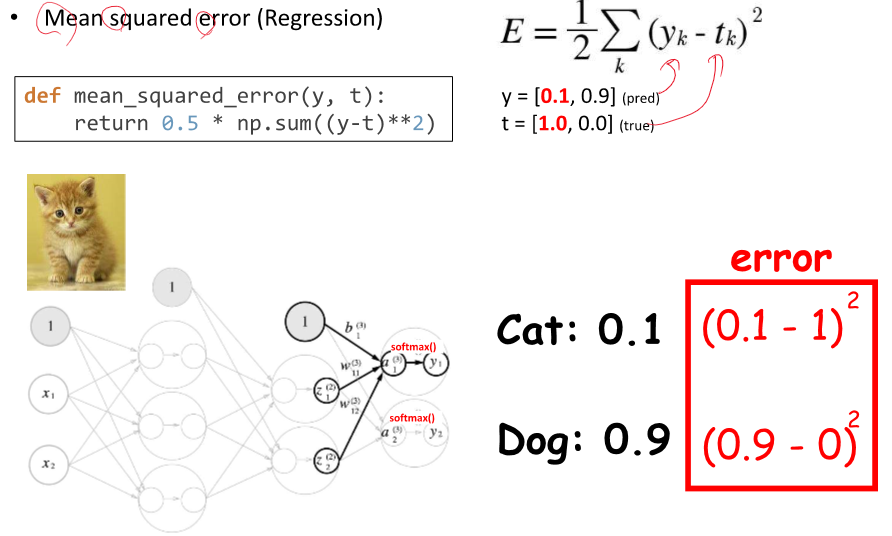

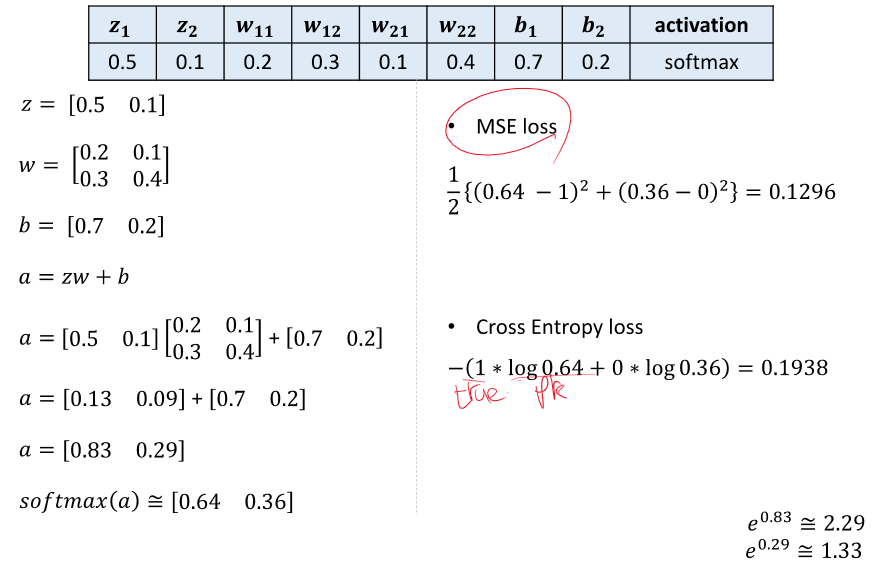

cross entropy loss를 줄이는 방향으로 학습한다.
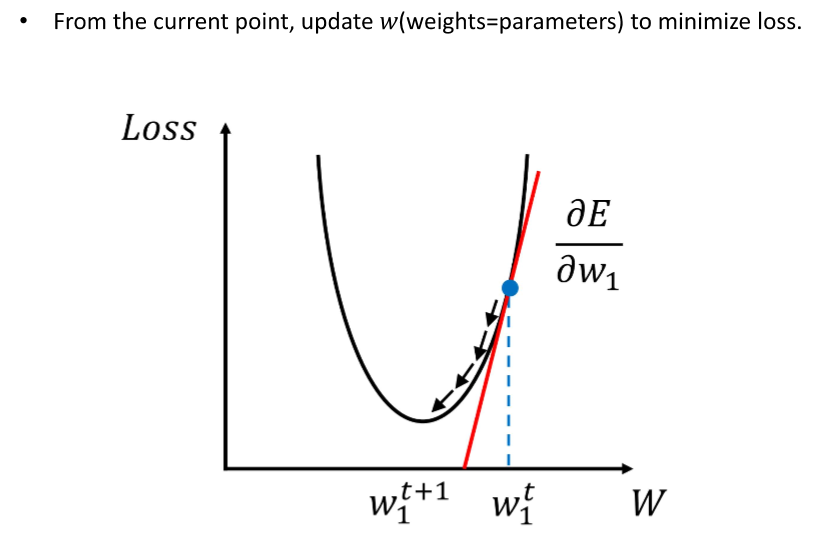
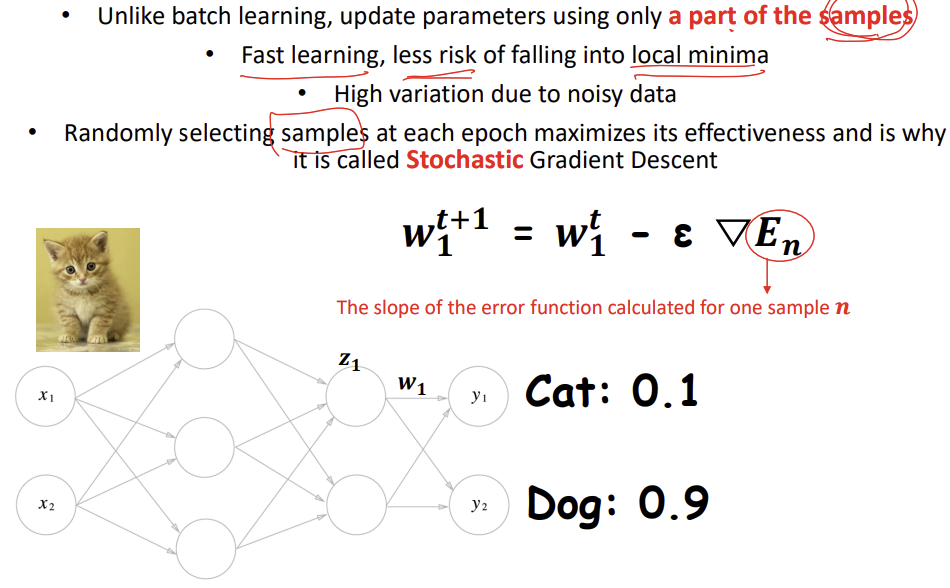
항상 경사 하강법을 사용하는 것은 아니다! 그러나 특정 상황에서만 쓴다.
네, 딥러닝에서 파라미터 최적화는 주로 손실 함수의 그래디언트(미분값)를 이용한 방법에 의존합니다. 이는 그래디언트 디센트 방법과 그 변형들이 딥러닝 모델의 학습에 널리 사용되는 이유입니다. 손실 함수의 그래디언트를 계산하고, 이를 사용해 모델의 가중치를 조정함으로써, 모델을 더 좋은 성능으로 이끌어갈 수 있습니다.
그래디언트 기반 방법 이외에도 몇 가지 다른 접근 방법이 있긴 하지만, 이들은 주로 특정 문제나 상황에 한정적으로 사용됩니다. 예를 들어:
- **유전 알고리즘(Genetic Algorithms)**: 자연 선택과 유전자 변이의 원리에 기초하여 최적화 문제를 해결합니다. 이 방법은 파라미터 공간을 무작위로 탐색하며, 성능이 좋은 "개체"의 특성을 다음 세대에 전달하여 점차 최적의 해를 찾아갑니다. 유전 알고리즘은 그래디언트 정보가 필요 없으나, 대규모 딥러닝 모델에는 비효율적일 수 있습니다.
- **베이지안 최적화(Bayesian Optimization)**: 목적 함수의 불확실성을 모델링하고, 이를 기반으로 파라미터를 조정합니다. 이 방법은 특히 하이퍼파라미터 최적화에 유용하게 사용됩니다. 그러나 베이지안 최적화 역시 큰 모델이나 데이터셋에는 계산 비용이 매우 높을 수 있습니다.
- **시뮬레이티드 어닐링(Simulated Annealing)**: 물리학의 어닐링 과정을 모방하여 최적화를 수행하는 방법입니다. 이 방법은 초기에는 높은 온도(큰 변화)에서 시작해 점차 온도를 낮추며(변화 폭을 줄이며) 최적점을 찾아갑니다. 특정한 상황에서 유용할 수 있으나, 일반적으로 큰 딥러닝 모델에는 적합하지 않습니다.
이러한 방법들은 그래디언트 기반 방법의 대안으로 사용될 수 있지만, 현재 딥러닝에서는 그래디언트 디센트와 그 변형이 최적화 문제를 해결하기 위한 가장 기본적이고 효율적인 도구로 간주됩니다. 그래디언트 기반 방법이 제공하는 정보(손실 함수의 기울기)를 활용하는 것이, 대부분의 경우에서 가장 정확하고 신속하게 모델을 최적화할 수 있는 방법이기 때문입니다.






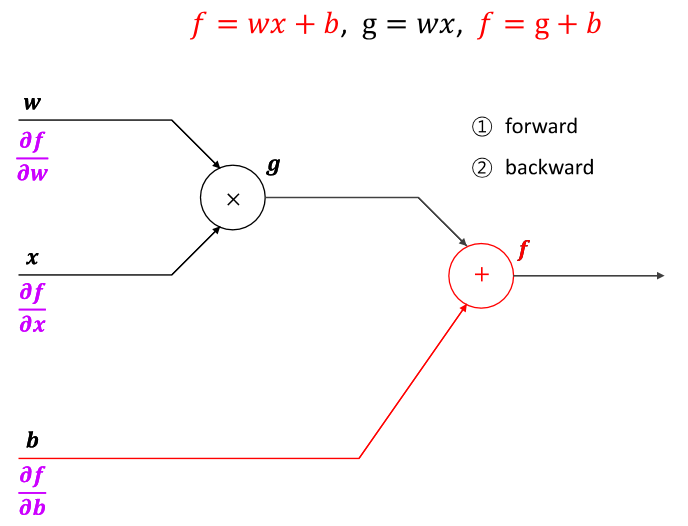
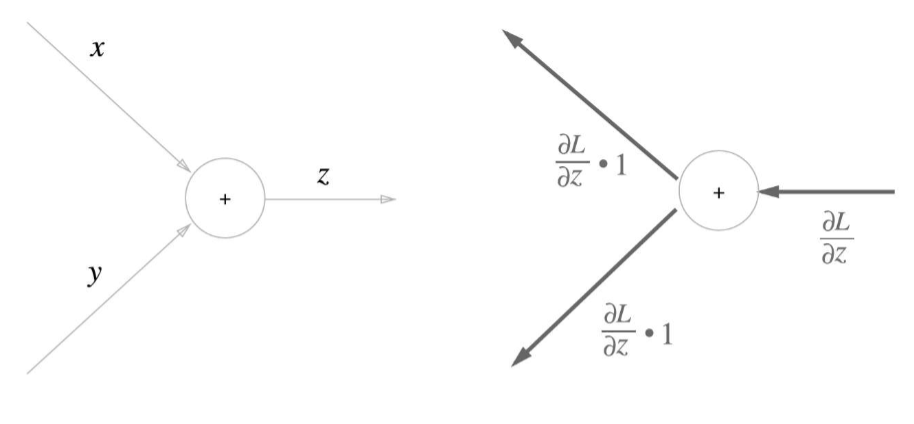
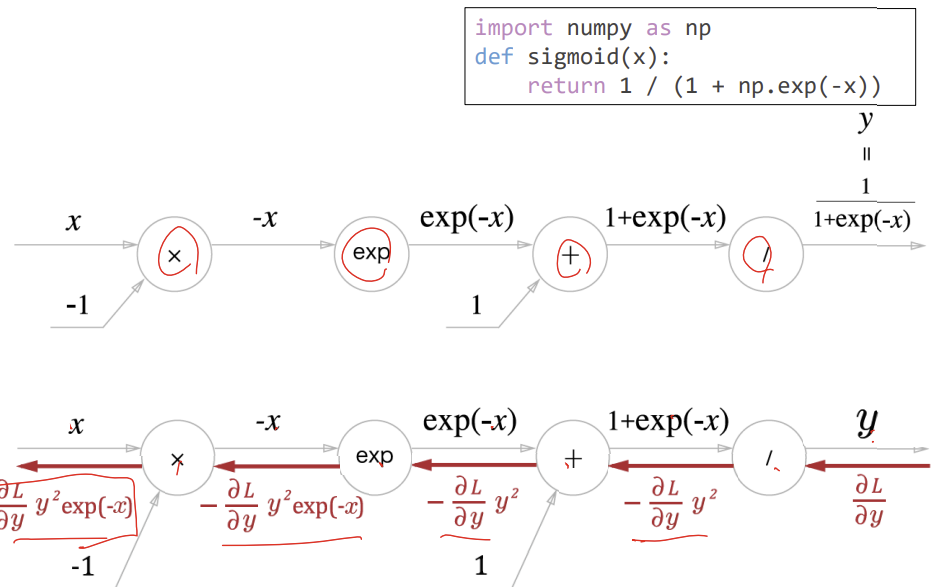
체인 룰을 사용하여 하나하나 미분하자!








'인공지능 > 자연어 처리' 카테고리의 다른 글
| 자연어 처리 정리 - 7강 Text classification with CNN (0) | 2024.04.13 |
|---|---|
| 자연어 처리 정리 - Deep learning recap 2 (0) | 2024.04.12 |
| 자연어 처리 정리 - 4강 word embedding 2 (0) | 2024.04.12 |
| 자연어 처리 정리 - 3강 Word embedding 1 (1) | 2024.04.12 |
| 자연어 처리 정리 - 2강 Text mining (0) | 2024.04.12 |