classification은 discrete한 부류 k중 n개를 선택하는 문제
binary = 둘 중 하나
multi class = 세 개 이상 중 1개
multi label = 두 개 이상 중 1개 이상
one class = k=1, n=1
지도학습,P(y|x) x가 주어졌을 때 y의 확률
가설 집합 Hypothesis set = decision boundary 이 것을 잘 찾아야 잘 분류한다.
확률을 근사하는 모델을 만들기 위해 모델은 0~ 1의 범위를 가지는 출력을 해야 한다=> sigmoid 사용

0과 1로 분류해준다.
기본적인 식들은 이미 이전 글에 다 작성해 놨기 때문에 그건 링크로 남겨놓겠다.
2023.12.13 - [인공지능/공부] - 인공지능 중간고사 개념 정리
음 깔끔하게 정리해 놓은 자료가 딱히 없네요...
그래도 저기 보면 다 있습니다.
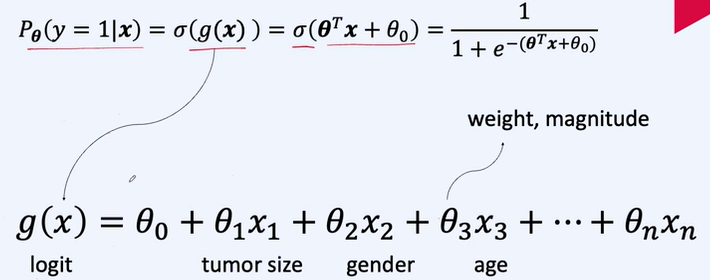
비용함수 -> 모델을 어떻게 학습해야 할까
model -> random variable = x와 parameter = theta로 구성되어 있다.
theta를 최대한 잘 찾아야 한다.
maximum Likehood Estimation, MLE 최대 우도 측정법
모델이 데이터 셋 D를 관측할 확률을 최대화할 수 있는 theta를 찾는 방법
확률은 0보다 작기 때문에 모두 곱하면 0에 가까워진다. -> negative log likelihood라는 방식을 사용해 곱이 아닌 합을 사용하여 최솟값을 찾기
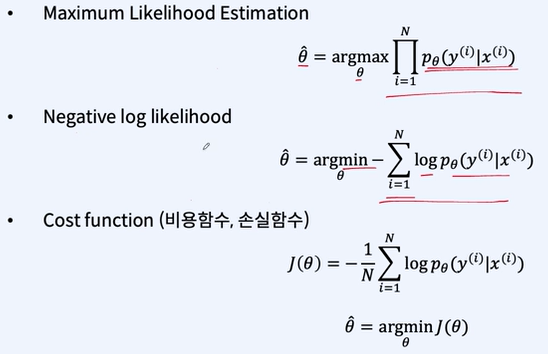
이제 위의 식을 풀면 우리가 익숙하게 보던 cross entropy cost function이 나오게 된다.
loss function -> 정답과 예측값의 차이
cost function -> 데이터 셋 전체에서 정답값과 예측값 차이의 평균
파라미터 학습
gradient descent : 함수를 theta에 대해 편미분 하여 기울기를 얻고 cost function J가 작아지는 방향으로 이동시킨다.
delta Learning Rule
이것도 위에 있는 정리 자료에 가보면 다 있는 자료이다.
피쳐 엔지니어링
특징(피쳐 feature)를 잘 추출해야한다.
numerical feature
- continuous
- discrete
Categorical feature
- Ordinal
- Nominal
Array feature
- image
- sound ....
Numerical feature
나이, 형제 수, 부모와 자식 수, 요금 등등
theta의 크기 차이가 많이 나면 느린 학습 수렴 속도를 가지게 된다.
스케일링을 통해 크기를 조절해줘야 한다.
scaling
- min-max feature scaling
최대를 1, 최소를 0으로 맞춰준다.
- mean normalization
최대를 0.5, 최소를 -0.5로 맞춰준다.
위 두개는 outlier에 민감하다. -> 극단 값 때문에 일반적인 값들 사이의 해상력이 떨어질 수 있다.
- standardization
극단값에 영향을 적게 받기 위해
x가 평균적인 다른 x에 대비하여 표준 편차의 몇배의 거리에 있는지로 정규화
bucketing
일정 구간의 숫자형 변수의 값들을 bucketing하여 일반화 되고 추상화된 특징을 추출 가능
ex)나이를 10살 단위로 묶어서 표현
Quantile Bucketing 각 구간에 동일한 사람들의 수
ChatGpt 답변
Bucketing:
개념: "Bucketing"은 데이터를 미리 정의된 구간(bucket)으로 나누는 방법입니다. 이 구간은 사용자가 정의하며, 일반적으로 동일한 크기를 가집니다.
용도: 일반적인 bucketing은 데이터를 균일한 크기의 구간으로 나누어 분석의 용이성을 높이거나, 카테고리화를 위해 사용됩니다.
예시: 예를 들어, 나이 데이터를 0-20, 21-40, 41-60 등과 같이 균일한 구간으로 나누는 경우가 bucketing에 해당합니다.
Quantile Bucketing:
개념: "Quantile Bucketing"은 데이터를 분위수(quantile)를 기준으로 나누는 방법입니다. 이 방법에서는 각 구간에 속하는 데이터의 수가 대략적으로 동일하도록 합니다.
용도: Quantile bucketing은 데이터의 분포가 균일하지 않은 경우에 유용합니다. 이 방법을 사용하면, 각 구간에 데이터가 고르게 분포되어, 특정 구간에 데이터가 몰리는 현상을 방지할 수 있습니다.
예시: 예를 들어, 소득 데이터를 4분위수(quantile)로 나누어 각 분위에 속하는 사람들의 수가 비슷하도록 하는 경우가 quantile bucketing에 해당합니다.
결론:
Bucketing은 구간의 크기가 일정하며 사용자에 의해 정의됩니다.
Quantile Bucketing은 데이터를 고르게 분포시키기 위해 분위수를 기준으로 구간을 나눕니다.
따라서, 이 두 방법은 데이터를 구간별로 나누는 목적은 같지만, 그 방법과 적용하는 상황에서 차이가 있습니다. Bucketing은 데이터의 균일한 분포를 가정할 때 유용하고, quantile bucketing은 데이터의 분포가 불균일할 때 더 적합합니다.
Categorical feature
- ordinal 순서와 영향이 있는 것(숫자와 비슷하다.)
- nominal 순서 X
카테고리도 숫자 부여해도 괜찮을까?
이진 카테고리는 0,1로 해도 된다.
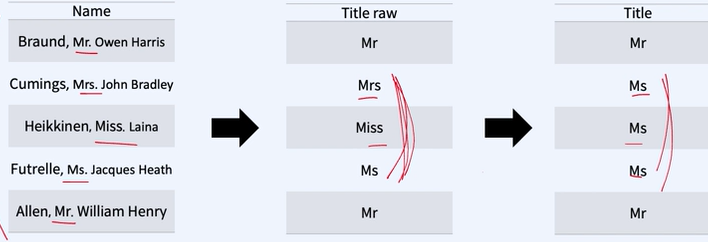
nominal은 linear classifier에 사용하기 부적합하다.(분류 선을 그리기가 애매하다.)
-> 각 카테고리를 별도의 이진 부류를 가진 변수들로 변형한다.

묶어서 더 일반화 시킬 수 있는 유사 카테고리일 경우 카테고리를 묶어 bucketing도 가능하다.
만약 결정 경계가 linear하지 않다면? = 원형이거나 2,3차 선이 필요하다.
->입력 변수에 거듭제곱을 하여 Polynomial feature를 만들면 nonlinear한 결정 경계를 정의할 수 있다.
Regularization
overfitting
과도한 결정경계의 학습 데이터 따라가기 = 이상치도 학습을 과하게 한다.
-> 학습데이터에 대해서만 좋은 성능을 내고, 실전에서는 성능이 오히려 떨어지는 경우
해결
모델을 단순하게 한다
- 최고 차항의 차수를 낮추기, feature 줄이기
Regularization
- 학습 파라미터 theta의 크기 억제
고차항의 theta의 크기를 작게 만들면 차수가 낮은 모델과 유사해진다. = 모델이 단순해진다.
이것도 사이트에 있는 내용입니당.

'인공지능 > 자연어 처리' 카테고리의 다른 글
| 자연어 처리 - Linear Regression 선형 회귀, Cost function 비용함수 실습 (1) | 2024.01.09 |
|---|---|
| 자연어 처리 - Logistic (0) | 2024.01.07 |
| 자연어 처리 - 머신러닝 기초, 나이브, k알고리즘, 앙상블, (1) | 2024.01.04 |
| 자연어 처리 - 모델 평가 (1) | 2024.01.03 |
| 자연어 처리 시작, 인공지능에 필요한 수학 개념 (2) | 2024.01.03 |