Using Degeneracy in the Loss Landscape for Mechanistic Interpretability

인공지능/논문 리뷰 or 진행

Using Degeneracy in the Loss Landscape for Mechanistic Interpretability - 논문리뷰

이게될까 2024. 11. 12. 00:15

728x90

Using Degeneracy in the Loss Landscape for Mechanistic Interpretability

Mechanistic Interpretability aims to reverse engineer the algorithms implemented by neural networks by studying their weights and activations. An obstacle to reverse engineering neural networks is that many of the parameters inside a network are not involv

arxiv.org

신경망의 해석 가능성을 방해하는 퇴행적 구조를 해결하기 위해, 이 논문은 Singular Learning Theory(SLT)와 Local Learning Coefficient(LLC)를 활용하여 퇴행성을 정의하고 분석합니다.

퇴행성은 활성화 벡터의 선형 의존성, 자코비안의 종속성, 그리고 뉴런 동기화를 포함하며, 이는 네트워크 내부 구조를 모호하게 만듭니다.

이를 해결하기 위해 Interaction Basis를 도입하여 퇴행성을 제거하고 계층 간 상호작용을 희소화해 해석 가능성을 높였습니다.

또한, 모듈화된 네트워크가 더 낮은 LLC를 가지며 해석과 일반화 성능에서 이점을 가질 수 있음을 이론적으로 제시했습니다.

이 논문은 복잡한 신경망 구조를 단순화하고, 이해 가능한 방식으로 재구성하는 데 중요한 방향성을 제공하지만 이해를 완벽하게 하진 못하겠네요...

1. 문제 정의

해결하려는 문제:
- 신경망의 메커니즘을 역설계하기 위한 해석 가능성 연구에서, 많은 네트워크 매개변수가 실제 계산에 사용되지 않고 퇴행적(degenerate) 구조를 이루어 신경망의 내부 구조를 이해하는 데 장애가 된다는 점을 해결하고자 함.
- 특히: 훈련된 신경망의 매개변수가 여러 조합으로 동일한 기능을 수행하는 경우, 이로 인해 해석 가능성이 저하됨.

2. 사용된 방법

Singular Learning Theory(SLT):
- 신경망의 매개변수 퇴행성을 이해하기 위해 **지역 학습 계수(Local Learning Coefficient, LLC)**를 확장하여 퇴행성을 측정.
- 퇴행성을 활용하여 네트워크 매개변수를 재구성해 모듈성(modularity) 및 상호작용 희소성(sparsity)을 도출.
Interaction Basis:
- 훈련 데이터에서 신경망 계층 간의 상호작용을 최소화하는 새로운 표현 방법을 제안.
- ReLU 기반 계층에서 활성화 벡터와 자코비안의 퇴행적 패턴을 분석하여 희소하고 해석 가능한 표현을 생성.

3. 주요 결과

퇴행성을 정의하고 신경망의 해석 가능성을 높이는 방법론을 제시:
- 세 가지 퇴행성 유형:
  1. 동일한 활성화 벡터 패턴.
  2. 유사한 자코비안 구조.
  3. ReLU 계층에서 동일한 firing 패턴을 보이는 뉴런 그룹.
- 이론적 발견:
  - 퇴행성이 높은 네트워크는 매개변수의 희소성이 증가하여 더 낮은 LLC를 가지며, 이는 더 나은 일반화 성능을 보장할 수 있음.
모듈성의 장점:
- 모듈형 네트워크는 상호작용이 적은 하위 네트워크로 분할되며, 이러한 구조는 더 낮은 LLC를 유도하여 더 해석 가능성이 높아짐.
실험적 결과:
- 제안한 Interaction Basis가 일부 퇴행성을 제거하며, 네트워크 상호작용을 희소하게 만드는 데 유용하다는 초기 증거를 제시.

4. 한계점

실용적 한계:
- Interaction Basis는 실제 신경망의 복잡한 구조에서 퇴행성을 완전히 제거하지 못할 수 있음.
- 비선형 활성화 함수와 비정형 데이터 분포에 대한 확장이 부족.
추가 연구 필요성:
- LLC 측정에서 임계값을 설정하는 방법론이 명확하지 않음.
- 모듈성과 상호작용 강도 간의 정량적 관계에 대한 추가 연구가 필요.

5. 논문의 타당성과 아쉬운 점

타당성:
- 퇴행성(degeneracy)이 신경망 해석 가능성에 미치는 영향을 체계적으로 탐구하며, SLT를 확장하여 이를 해결하려는 시도는 학문적으로 의미가 있음.
- 모듈성과 희소성 기반 해석 가능성 증가 전략은 직관적이고 합리적.
아쉬운 점:
- Interaction Basis와 모듈성 평가 방법이 초기 단계로, 실용적 성능 평가가 제한적.
- 실제 신경망의 복잡한 상호작용을 더 정교하게 반영할 필요가 있음.

연구 적용 방안

이 논문에서 제안된 퇴행성 분석과 모듈성 접근법은 **Sparse Autoencoder(SAE)**나 Mixture of Experts(MoE) 모델에 응용 가능할 것입니다. 특히:

Bias 제거 실험: Interaction Basis를 사용해 특정 편향된 기능을 제거하고, 모델의 생성 능력 유지 여부를 평가.
모듈성 기반 해석: 모듈화된 구조를 통해 복잡한 신경망을 분할하여 설명 가능성을 증진.
LLC 최적화: LLC를 측정하고 감소시켜 네트워크 해석성을 높이는 방향으로 실험 설계.

퇴행적 구조를 이룬다는 것이 어떻게 되는거야?
쓸모 없는 연산을 진행한 다는 것이야?

"퇴행적(degenerate) 구조"라는 것은 신경망의 매개변수나 구조가 중복되거나 실제 계산에 실질적으로 기여하지 않는 부분을 포함하고 있다는 뜻입니다. 이를 통해 쓸모없는 연산이 진행된다고 단정하기보다는, 같은 출력을 내기 위해 다양한 매개변수 조합이 가능하거나, 특정 매개변수가 사실상 사용되지 않는 경우를 말합니다. 이로 인해 신경망의 내부 작동을 이해하기 어렵게 만드는 문제를 야기합니다.

구체적으로 퇴행적 구조가 의미하는 것:

활성화 벡터의 선형 의존성:
- 한 계층의 뉴런들이 생성하는 활성화 벡터들이 선형적으로 종속되어 있다면, 일부 뉴런은 새로운 정보를 추가하지 않고 기존 뉴런의 조합으로 표현됩니다.
- 즉, 네트워크의 계산이 불필요하게 복잡해지고 해석이 어려워집니다.
자코비안(Jacobian)의 선형 의존성:
- 역전파(Backpropagation) 중에 사용되는 그래디언트들이 선형적으로 의존적일 경우, 실제로 학습에 기여하지 않는 매개변수가 존재할 수 있습니다.
- 이러한 매개변수들은 네트워크의 출력에 거의 영향을 미치지 않으므로 "유휴 상태"로 간주됩니다.
동기화된 ReLU 뉴런:
- 같은 데이터 포인트에서 항상 동일하게 "켜지거나 꺼지는" 뉴런들이 존재하는 경우, 이러한 뉴런들은 동일한 기능을 수행하기 때문에 독립적인 역할을 하지 않습니다.
- 결과적으로, 네트워크의 일부 뉴런은 계산에 기여하지 않으면서 매개변수 공간만 낭비하게 됩니다.

퇴행적 구조의 영향

모델 해석성 저하:
- 신경망의 내부에서 실제 계산에 사용되지 않는 매개변수들이 많아질수록, 어떤 매개변수가 핵심적인 역할을 하는지 파악하기 어려워집니다.
불필요한 매개변수 증가:
- 매개변수 공간이 커지면서 과적합 위험이 증가하거나 학습 속도가 느려질 수 있습니다.
일반화 가능성 증가 (긍정적 측면):
- 단순히 매개변수의 퇴행성이 증가한다고 해서 항상 부정적인 것은 아닙니다.
- Singular Learning Theory(SLT)에서는 퇴행성이 증가하면 손실 함수의 최소값 주변에 더 넓은 "안정된 영역"이 형성되어 일반화 성능이 향상될 수 있다고 제안합니다.

쓸모없는 연산과는 다릅니다

"쓸모없는 연산"은 단순히 불필요한 계산이 포함되었음을 의미하지만, 퇴행적 구조는 네트워크의 매개변수 공간이 실제 계산보다 과도하게 복잡하거나 중복된 표현을 가지는 상황을 가리킵니다. 즉:

퇴행적 구조는 출력에는 영향을 미치지 않으면서도 중복되거나 덜 중요한 계산이 포함된 상황을 설명합니다.

정리

퇴행적 구조는 네트워크 내부의 중복성과 비효율성을 나타내며, 이를 해결하면 네트워크의 해석 가능성과 계산 효율성을 높일 수 있습니다. 그러나 이 구조가 일반화 성능을 높이는 경우도 있으므로 신중히 평가해야 합니다.

그럼 여기선 퇴행적 구조 때문에 중첩이 커져서 모델을 해석 하기힘들어 진다는 것이네?
그리고 퇴행성이 증가하면 일반화 성능이 향상될 수 있지만 불필요한 매개변수가 증가해서 과적합이나 학습속도가 느려질 수 있는 거고?

네, 맞습니다! 이를 조금 더 체계적으로 정리해 보겠습니다.

1. 퇴행적 구조와 모델 해석성의 어려움

핵심 문제: 퇴행적 구조는 신경망 내부에서 특정 매개변수들이 실제로 사용되지 않거나, 중복된 계산을 하면서 결과적으로 모델의 기능적 역할과 구조를 파악하기 어렵게 만듭니다.
- 예: 활성화 벡터나 그래디언트가 선형적으로 의존적인 경우, 어떤 뉴런이나 매개변수가 실제로 기여하는지 판단하기 어려워짐.
- 이로 인해 신경망의 메커니즘 역설계(reverse engineering)가 복잡해지고, "이 모델이 왜 이렇게 작동하는가?"라는 질문에 답하기 어려워집니다.

2. 퇴행성과 일반화 성능의 관계

긍정적 영향:
- 퇴행성이 증가하면 일반화 성능이 향상될 가능성이 있습니다.
- 이유: 퇴행성이 높으면 손실 함수의 최소값 주변에 더 넓은 안정 영역(basin)이 형성되므로, 모델이 새로운 데이터에 대해 더 견고하게 반응할 가능성이 커집니다.
  - 넓은 안정 영역: 여러 매개변수 조합이 동일한 출력을 내므로, 훈련 데이터에 과도하게 민감하지 않음.
- 이는 Singular Learning Theory(SLT)의 주요 주장 중 하나입니다.

3. 퇴행성의 부정적 영향

불필요한 매개변수 증가:
- 퇴행성으로 인해 모델에 사용되지 않거나 중복된 매개변수가 많아질 경우, 매개변수 공간이 비효율적으로 커집니다.
- 결과적으로:
  1. 과적합 위험 증가: 훈련 데이터에 지나치게 맞추는 경향이 생길 수 있음.
  2. 학습 속도 저하: 더 큰 매개변수 공간을 탐색해야 하므로 학습 효율성이 떨어짐.

4. 요약 및 균형점 찾기

요점: 퇴행성은 두 가지 상충된 효과를 가질 수 있습니다.
1. 일반화 성능 향상: 모델이 다양한 상황에 대응할 수 있도록 만듦.
2. 해석성 및 효율성 저하: 불필요한 매개변수 증가와 중복성으로 인해 구조 파악과 학습이 어려워짐.
해결 방향:
- 퇴행성을 활용해 일반화 성능을 유지하면서, 불필요한 매개변수를 최소화하는 방법이 필요.
- 논문에서는 이를 위해 Interaction Basis를 도입하여 퇴행적 구조를 제거하고 모델의 해석성을 높이려고 시도합니다.

결론

퇴행성은 신경망 해석성에서 부정적 영향을 미치지만, 일반화 성능에서는 긍정적 효과를 가질 수 있는 양날의 검입니다. 따라서, 퇴행성을 완전히 없애기보다는 해석성을 높이고 계산 효율성을 유지하면서 일반화 성능을 희생하지 않는 방식으로 적절히 제어하는 것이 핵심입니다.

그럼 이 논문에서 사용한 방법인 SLT와 Interaction Basis에 대해 좀 더 자세하게 논문을 기반으로 설명해줘

1. Singular Learning Theory(SLT)의 개념 및 역할

SLT(Singular Learning Theory)는 신경망의 매개변수 공간에서 퇴행적(degenerate) 구조를 수량화하고, 이를 통해 모델의 학습 및 일반화 특성을 설명하려는 이론입니다. 이 논문에서는 SLT를 기반으로 네트워크의 퇴행성을 측정하고, 이를 신경망 해석성에 적용합니다.

SLT의 핵심 요소:

학습 계수(learning coefficient, λ):
- 손실 함수의 최소값 주변에서 매개변수 공간이 얼마나 넓게 펼쳐져 있는지를 나타내는 지표.
- λ가 낮을수록 손실 함수의 최소값 주변 영역이 넓고, 더 많은 퇴행성을 의미.
- 퇴행성이 높으면 일반화 성능이 향상될 가능성이 큼.
지역 학습 계수(Local Learning Coefficient, LLC):
- SLT는 글로벌 최소값에 대해 λ를 정의하지만, 실제 신경망은 지역적인 최소값(local minimum)을 가지는 경우가 대부분.
- LLC(λ̂)는 특정 지역 최소값의 퇴행성을 측정하는 도구로, 모델의 실제 학습 상태를 반영.

논문에서 SLT의 확장:

이론적인 λ와 LLC는 무한 데이터와 완전 수렴 상태를 가정하지만, 현실에서는 훈련 데이터와 손실이 유한합니다.
이를 해결하기 위해:
- 행동 손실(Behavioral Loss): 두 네트워크가 동일한 입력에 대해 얼마나 유사한 출력을 내는지 측정하여, 실제 훈련 데이터에서 퇴행성을 수량화.
- 유한 데이터 SLT: λ를 무한 데이터가 아닌 유한 데이터 상황에서 재해석, 매개변수 공간의 퇴행적 자유도를 더 현실적으로 측정.

2. Interaction Basis의 정의 및 역할

Interaction Basis는 신경망의 계층 간 상호작용을 재구성하여 퇴행성을 줄이고 해석성을 높이기 위해 도입된 방법입니다.

핵심 아이디어:

신경망의 계층 간에 발생하는 퇴행적 구조를 분석하여, 선형적 또는 비선형적으로 의존적인 활성화 패턴과 그래디언트 패턴을 제거.
매개변수 공간을 효율적으로 표현할 수 있는 새로운 기준(basis)을 생성하여, 모델의 상호작용을 희소화(sparsify)하고 해석을 용이하게 만듦.

구체적인 접근법:

활성화 벡터의 차원 축소:
- 특정 계층에서 활성화 벡터가 선형적으로 의존적이라면, 이를 PCA(주성분 분석) 또는 유사한 기법을 사용해 저차원으로 표현.
- 예: 계층의 활성화 벡터가 n차원 공간에 있지만 실제로는 r차원 공간(r < n)을 차지한다면, r개의 주성분만 남기고 나머지를 제거.
자코비안(Jacobian)의 재구성:
- 역전파 단계에서 자코비안 행렬이 선형적으로 의존적이라면, 불필요한 자유도를 제거하여 계산 효율성을 높임.
- 자코비안의 Gram 행렬을 기반으로 축소된 공간을 생성.
ReLU 뉴런의 동기화(Synchronization) 해결:
- 동일한 데이터 포인트에서 항상 "켜지거나 꺼지는" 뉴런 그룹을 통합하여, 동일한 계산을 반복하지 않도록 처리.

Interaction Basis의 특징:

각 계층의 활성화와 가중치를 재구성하여 새로운 상호작용 공간(interaction space)을 정의.
특정 상호작용이 제거되거나 희소화됨으로써, 네트워크의 구조적 해석이 용이해짐.
예: 동일한 계층 내에서의 상호작용뿐 아니라 인접 계층 간의 불필요한 상호작용도 줄임.

3. SLT와 Interaction Basis의 연계

논문에서는 SLT와 Interaction Basis를 결합하여, 신경망의 퇴행성을 분석하고 해석성을 높이는 데 사용합니다.

SLT로 퇴행성 분석:
- SLT를 통해 퇴행성(degeneracy)의 근본 원인을 파악: 선형 의존성, 동기화된 뉴런, 불필요한 매개변수 등.
Interaction Basis로 해결:
- SLT로 분석한 퇴행성을 줄이기 위해 Interaction Basis를 활용.
- 매개변수를 재구성하여 퇴행성을 제거하고 상호작용을 희소화.

4. 적용 및 장점

모듈성(Modularity):
- Interaction Basis는 퇴행성을 줄이는 동시에 네트워크를 독립적인 모듈로 분할하여, 전체 구조를 이해하기 쉽게 만듦.
희소화(Sparsity):
- 퇴행성을 줄임으로써, 계층 간 상호작용을 최소화.
- 예: 활성화 벡터 또는 자코비안의 저차원 표현을 통해, 실제로 중요한 계산만 남김.
해석 가능성:
- 불필요한 매개변수와 계산을 제거하므로, 신경망의 작동 원리를 더 명확히 이해할 수 있음.
계산 효율성:
- 매개변수 공간이 축소되므로 학습 속도와 계산 효율이 개선.

요약

SLT는 신경망의 퇴행적 자유도를 정량화하여, 모델의 일반화 성능과 해석 가능성 간의 관계를 이해하는 데 사용됩니다.
Interaction Basis는 SLT로 분석된 퇴행성을 줄이는 실질적 방법으로, 신경망의 구조를 더 희소화하고 해석 가능성을 높입니다.
두 방법은 결합하여, 모델의 해석성을 높이고 불필요한 계산을 줄이며, 일반화 성능을 유지하는 데 기여합니다.

SLT는 학습 계수를 통해 퇴행성을 측정하고, LLC는 특정 지역의 퇴행성을 측정한거네?
또한 손실을 무한히 줄일 수 있을 것 같지만 현실에서는 데이터의 제한 때문에 손실이 유한하여 그 것을 좀 더 정량화 한 것이네?

네, 정확합니다! 이를 체계적으로 정리하면 아래와 같습니다.

1. SLT와 학습 계수(λ)의 역할

학습 계수(learning coefficient, λ):
- SLT의 핵심 지표로, 손실 함수의 최소값 주변에서 매개변수 공간이 얼마나 넓게 펼쳐져 있는지를 측정.
- λ가 낮을수록 퇴행성이 높음: 매개변수 공간에서 다양한 조합이 동일한 출력을 생성할 수 있다는 뜻.
- 넓은 손실 함수 영역(넓은 basin)은 모델이 새로운 데이터에 더 잘 일반화할 가능성을 높임.

2. LLC(Local Learning Coefficient)의 역할

SLT는 기본적으로 손실 함수의 글로벌 최소값(global minimum)을 가정하여 λ를 정의하지만, 실제 신경망 훈련에서는 지역 최소값(local minimum)이 더 흔하게 발생.
LLC(λ̂):
- 특정 지역 최소값 주변의 퇴행성을 측정하기 위해 λ를 확장한 개념.
- 손실 함수의 최소값 주변의 매개변수 공간에서 실제로 사용되는 매개변수와 사용되지 않는 매개변수를 구분하는 데 유용.

3. 현실적 한계와 확장

SLT는 이론적으로 무한한 데이터와 완벽한 학습(손실이 0에 가까운 상태)을 가정하지만, 현실에서는 다음과 같은 한계가 존재합니다:

데이터 제한:
- 실제 훈련 데이터는 유한하므로, 모델이 정확히 수렴하지 않고 손실이 일정 수준에서 멈춤.
- 매개변수 공간에서 "노이즈"가 존재하여 훈련되지 않은 영역이 발생.
손실의 비대칭성:
- SLT는 손실 함수가 매끄럽고 대칭적이라고 가정하지만, 실제 신경망의 손실 함수는 비선형적이고 복잡함.

이를 해결하기 위한 접근:

행동 손실(Behavioral Loss):
- 네트워크가 동일한 입력에 대해 얼마나 유사한 출력을 내는지 측정하는 새로운 손실 함수를 정의.
- 이 손실은 매개변수의 세부적인 차이보다는 출력의 유사성에 초점을 맞춰, 퇴행성을 더 현실적으로 측정.
유한 데이터 SLT(Finite Data SLT):
- 손실 함수의 ε-범위(ε-cutoff)를 도입하여, 손실이 무한히 줄어들지 않고 특정 유한한 수준에서 평가.
- 예를 들어, ε 값이 클수록 더 많은 매개변수 조합이 동일한 손실을 가지므로, 이를 기반으로 퇴행성을 정량화.

4. 결론: 현실에서의 퇴행성 정량화

SLT:
- 학습 계수 λ는 네트워크의 퇴행성을 정량화하여, 손실 함수의 안정 영역(basin)이 넓을수록 일반화 성능이 좋아질 수 있음을 설명.
- 이론적으로는 무한한 데이터와 완벽한 수렴을 가정.
LLC:
- 현실적인 지역 최소값에서의 퇴행성을 측정하며, 특정 손실 범위 내에서 매개변수의 다양성을 평가.
현실적 확장:
- 유한 데이터와 손실 함수의 복잡성을 고려하여, ε-범위와 행동 손실을 도입해 퇴행성을 더 실질적으로 측정.
- 이는 실제 신경망 훈련에서 발생하는 "노이즈"와 "불완전한 학습"을 반영한 개선된 방식.

추가 요점

결국 SLT와 LLC는 퇴행성(degeneracy)의 본질을 이해하고 이를 활용하거나 해결하는 데 중요한 이론적 도구입니다. 데이터 제한으로 인해 손실이 유한한 상황에서도 이러한 도구를 사용해 신경망의 구조적 복잡성을 정량화하고, 일반화 성능과 해석 가능성을 높이는 방향으로 활용할 수 있습니다.

Interaction Basis를 통해 계층 간 상호작용을 재구성하여 퇴행성을 줄이고 해석성을 높인다고 하는데 이해가 잘 안가네
Interaction Basis를 논문에 기반해서 좀 더 자세하게 설명해줘

Interaction Basis란 무엇인가?

Interaction Basis는 신경망의 계층 간 상호작용(interaction)을 재구성하여 퇴행성을 줄이고, 결과적으로 모델의 해석 가능성을 높이는 방법입니다. 논문에서는 특정 계층에서 발생하는 불필요하거나 중복된 계산(퇴행성)을 최소화하고, 계층 간 상호작용을 단순화하여 희소한 표현(sparse representation)을 만들고자 합니다.

1. Interaction Basis의 핵심 아이디어

퇴행성 제거:
- 신경망에서 일부 매개변수나 계산은 출력에 실질적인 영향을 미치지 않음.
- 이러한 불필요한 요소들을 분석하고 제거함으로써, 모델의 핵심 계산만 남기는 방식.
희소화(Sparsification):
- 계층 간의 상호작용에서 의미 없는 연결(예: 선형 의존성)을 제거하여 상호작용 구조를 단순화.
- 상호작용의 구조를 최소화함으로써, 모델의 작동 방식을 더 쉽게 해석 가능.
재구성(Reconstruction):
- 활성화 벡터와 자코비안(Jacobian) 행렬을 새로운 기준(basis)으로 변환하여, 각 계층의 중요한 특징만 남김.
- 이로써 모델 내부의 정보를 더 직관적이고 해석 가능한 방식으로 표현.

2. Interaction Basis의 구현 과정

Interaction Basis는 다음 세 단계로 구성됩니다.

(1) 활성화 벡터의 차원 축소

문제:
- 특정 계층에서 활성화 벡터(뉴런의 출력)가 선형적으로 의존적이라면, 일부 뉴런의 출력이 새로운 정보를 추가하지 않음.
- 예: 10개의 뉴런이 있지만 실제로는 5개만 독립적인 정보를 담고 있다면, 나머지 5개는 중복.
해결:
- PCA(주성분 분석) 또는 유사한 방법을 사용해 선형적으로 독립적인 벡터만 남기고, 나머지를 제거.
- 활성화 벡터의 Gram 행렬을 분석하여, 고유값(eigenvalues)이 작은 축은 제거.
- 이렇게 하면 뉴런의 활성화 공간을 저차원으로 표현 가능.

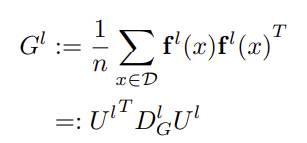
(2) 자코비안(Jacobian)의 희소화

문제:
- 역전파 단계에서 자코비안 행렬(각 계층의 가중치 변화가 출력에 미치는 영향을 나타냄)이 선형적으로 의존적이라면, 일부 가중치는 학습에 실질적으로 기여하지 않음.
- 예: 자코비안의 특정 열 또는 행이 다른 것들과 선형 조합이라면, 해당 방향은 불필요한 계산.
해결:
- 자코비안의 Gram 행렬에서 고유값이 작은 축을 제거.
- 이 과정으로 역전파 계산에서 불필요한 자유도를 줄이고, 효과적인 매개변수만 남김.

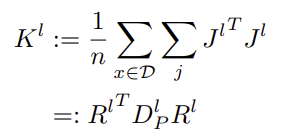
(3) 동기화된 뉴런 그룹 처리

문제:
- 특정 계층의 ReLU 뉴런들이 항상 동일하게 활성화되거나 비활성화되는 경우, 이러한 뉴런들은 실제로 독립적인 계산을 하지 않음.
- 예: 뉴런 A와 B가 항상 동일한 firing 패턴(동일 데이터 포인트에서 동시에 켜지고 꺼짐)을 가진다면, 둘 중 하나만 남겨도 됨.
해결:
- 뉴런의 firing 패턴을 분석하여 동기화된 뉴런을 묶고, 이를 하나의 단위로 통합.
- 뉴런 동기화는 다음과 같은 방법으로 처리:
  - 뉴런 그룹 Sa를 생성하여 동일한 패턴을 가진 뉴런들을 하나로 묶음.
  - 뉴런 그룹별로 독립적인 정보를 보존하면서 중복 계산 제거.

3. Interaction Basis의 결과

희소화된 계층 간 상호작용

Interaction Basis는 계층 간 상호작용을 재구성하여, 불필요한 연결을 줄이고 희소한 표현을 생성.
재구성된 계층 간 연결은 다음과 같은 특징을 가짐:
1. 불필요한 뉴런 제거: 중복된 활성화나 계산이 제거되어 주요 정보만 남음.
2. 희소한 상호작용: 각 계층 간 연결에서 상호작용의 수가 줄어듦.
3. 가중치 행렬의 단순화: 새로운 기준으로 표현된 가중치 행렬은 더 적은 독립적인 매개변수를 가짐.

계층 간 상호작용 그래프

Interaction Basis는 각 계층의 노드를 그래프 형태로 표현하여, 상호작용을 더 명확하게 보여줌.
예:
- 각 노드는 독립적인 활성화 벡터를 나타냄.
- 그래프의 간선은 계층 간 상호작용을 나타내며, 간선의 수는 희소화 과정을 통해 최소화.

4. Interaction Basis의 한계

완벽한 비선형성 처리 부족:
- Interaction Basis는 선형적 의존성을 중심으로 재구성하므로, 완벽히 비선형적인 상호작용에 대해서는 효과가 제한될 수 있음.
실제 데이터에서의 평가:
- 논문에서 제시된 방법론은 이론적 기반이 강하지만, 실제 대규모 신경망에서의 평가가 아직 초기 단계.

5. 요약

Interaction Basis는 계층 간 상호작용을 재구성하여 퇴행성을 줄이고, 신경망의 구조를 더 희소하고 직관적으로 만드는 방법입니다. 이를 통해:

불필요한 매개변수와 계산을 제거하여 해석 가능성을 높임.
계층 간 상호작용을 단순화하여 신경망의 메커니즘을 더 쉽게 이해할 수 있음.
결과적으로 모델의 계산 효율성과 해석 가능성을 모두 개선할 수 있습니다.

예시를 들어서 좀 더 설명해줄 수 있어?

네! Interaction Basis의 작동 원리를 예시를 들어 설명하겠습니다. 예시는 계층 간 활성화 벡터와 뉴런 동기화의 처리 방식을 중심으로 다룹니다.

1. 활성화 벡터의 차원 축소

예시: 활성화 벡터가 선형적으로 의존적인 경우

문제 상황:
- 신경망의 한 계층에서 활성화 벡터가 다음과 같이 주어졌다고 가정합시다: fl(x)=[a,2a,b,a+b]
  - 여기서 a와 b는 독립적인 정보입니다.
  - 2a와 a+b는 a와 b의 선형 조합이므로, 독립적인 정보를 추가하지 않습니다.
해결 방법:
1. 활성화 벡터의 Gram 행렬을 계산합니다:
  - 이 행렬은 활성화 벡터 간의 상호작용을 나타냅니다.
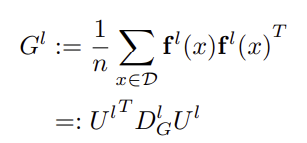
    Gram 행렬
2. PCA(주성분 분석)를 통해 고유값이 큰 축만 남깁니다:
  - 와 는 고유값이 크므로 유지.
  - 2a와 a+b는 선형 의존성이 크므로 제거.
3. 남은 활성화 벡터는: freducedl(x)=[a,b]
결과:
- 차원 축소를 통해 불필요한 뉴런 출력을 제거하여, 중요한 정보만 남깁니다.
- 다음 계층으로 전달되는 정보가 단순화되고, 해석 가능성이 높아집니다.

2. 뉴런 동기화의 처리

예시: 동기화된 뉴런 그룹

문제 상황:
- ReLU 활성화 함수가 있는 신경망에서 다음 뉴런들이 있다고 가정합니다:
  - 뉴런 A: 특정 데이터 포인트에서 항상 켜짐 (fAl(x)>0)
  - 뉴런 B: 뉴런 A가 켜질 때마다 항상 동일한 값 출력 (fBl(x)=fAl(x))
  - 뉴런 C: 독립적인 정보를 출력.
- 여기서 뉴런 A와 B는 동기화되어 있고, 독립적인 정보를 추가하지 않으므로 뉴런 B는 제거 가능.
해결 방법:
1. 뉴런의 활성화 패턴을 분석:
  - 뉴런 A와 B의 활성화 패턴이 동일하므로, 하나로 통합 가능.
2. 뉴런 그룹 Sa 생성:
  - A와 B를 하나의 그룹으로 묶고, 해당 그룹의 대표 뉴런만 남김.
3. 재구성 후 출력: freducedl(x)=[fAl(x),fCl(x)]
결과:
- 뉴런 B는 계산에서 제외되며, 모델의 복잡성이 줄어듭니다.
- 그룹화된 정보는 더 해석 가능하게 변환됩니다.

3. 계층 간 상호작용의 희소화

예시: 희소화된 계층 간 연결

문제 상황:
- 두 계층 간의 가중치 행렬이 다음과 같이 주어졌다고 가정합니다: Wl→l+1=[10200102]
  - 활성화 벡터 fl(x)가 [a,b,a+b,b+a]라고 가정.
  - Wl→l+1에서 일부 연결이 불필요하게 중복되어 있음.
해결 방법:
1. 활성화 벡터 fl(x)를 Interaction Basis로 변환:
  - freducedl(x)=[a,b]만 남김 (선형 의존 제거).
2. Wl→l+1도 재구성:
  - 재구성된 Wl→l+1:
결과:
- 상호작용이 단순화되고, 중요한 연결만 유지됩니다.
- 계산량이 감소하며, 네트워크의 구조적 해석이 더 명확해집니다.

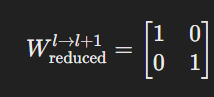
4. Interaction Basis의 직관적 이해

Interaction Basis를 통해 다음과 같은 결과를 얻습니다:

불필요한 활성화 제거:
- 계층 내 활성화 벡터나 뉴런의 선형 의존성을 제거하여, 중요한 정보만 남김.
희소한 연결:
- 계층 간 가중치 행렬을 단순화하고, 의미 있는 상호작용만 유지.
계층 간 해석 용이성:
- 복잡했던 연결 구조를 단순화하여, 모델의 작동 원리를 직관적으로 이해 가능.

이 예시를 통해 Interaction Basis가 신경망의 퇴행적 구조를 제거하고, 계층 간 상호작용을 단순화하며, 계산 효율성과 해석 가능성을 동시에 높이는 과정을 이해할 수 있습니다. 추가 질문이 있으면 말씀해주세요!

이렇게 되면 모델 구조가 바뀌니까 학습 자체도 다시 해야 하는 것 아니야?

좋은 질문입니다! Interaction Basis를 적용하는 것이 모델 구조를 바꾸는 것처럼 보일 수 있지만, 이 과정은 모델 학습 자체를 다시 시작해야 하는 것과는 다릅니다. 이를 단계별로 설명하겠습니다.

1. Interaction Basis는 모델 재구성이지만, 학습 결과는 유지

Interaction Basis는 학습된 신경망의 매개변수와 활성화 표현을 재구성하는 것이지, 모델을 처음부터 다시 학습시키는 것이 아닙니다.
- 학습 후 모델의 매개변수(가중치와 편향 등)와 활성화 벡터를 새로운 기준으로 변환.
- 즉, 출력 결과는 동일하지만 표현 방식이 달라짐.
- 이는 신경망의 재파라미터화(reparameterization) 과정에 해당합니다.

예시

기존 모델에서 학습된 계층 간 가중치: Wl→l+1
Interaction Basis로 변환 후: W′l→l+1=TlWl→l+1Tl+1−1
- Tl, Tl+1는 각 계층의 Basis Transformation 행렬.
- 변환된 가중치 W′는 원래 W와 동일한 기능을 수행하지만, 새로운 기준으로 표현.

2. 학습이 다시 필요하지 않은 이유

출력 행동이 동일:
- Interaction Basis를 적용해도 입력-출력 맵핑(input-output mapping)은 변하지 않습니다.
- 모델이 수행하는 기능은 그대로 유지되므로 추가 학습이 필요하지 않습니다.
기존 학습 데이터 활용 가능:
- 재구성된 모델은 기존 학습 데이터를 기반으로 성능을 유지합니다.
- 학습이 끝난 후 퇴행적 구조를 단순화하는 것이므로, 기존 데이터와의 호환성이 보장됩니다.

3. Interaction Basis가 학습 과정에 미치는 영향

Interaction Basis는 학습 과정에 다음과 같은 긍정적인 영향을 미칠 수 있습니다:

(1) 훈련 후 재구성

학습이 끝난 후 적용하면:
- 모델을 희소화하고, 구조를 간결하게 만들어 해석 가능성과 추론 효율성을 높임.
- 예: 불필요한 뉴런이나 연결 제거 후, 더 효율적인 형태로 추론 가능.

(2) 학습 중간에 적용

학습 중간 단계에서 적용한다면:
- 퇴행적 구조를 제거해 모델의 매개변수 공간을 효율적으로 탐색.
- 예: 중복된 뉴런이나 선형 의존성을 제거하면, 학습 속도가 빨라질 가능성.
- 하지만 이 경우, 학습 안정성을 보장하기 위해 추가적인 설계가 필요할 수 있음.

4. Interaction Basis의 적용은 구조 변경과 다릅니다

Interaction Basis는 모델의 구조 자체를 변경하지 않습니다. 오히려 다음과 같은 점에서 구조적 안정성을 유지합니다:

출력 맵핑 보존:
- 모델의 입력과 출력 간 관계는 동일.
- 이를 통해 학습 결과를 그대로 유지 가능.
모듈성 강조:
- Interaction Basis를 통해 계층 간 상호작용을 단순화하면, 각 계층의 독립적인 역할이 명확해짐.

5. Interaction Basis와 새로운 학습의 필요성 비교

특징Interaction Basis 적용새로 학습

학습 데이터 재사용 여부	기존 학습 데이터와 결과 그대로 유지	새로 학습 데이터를 필요로 함
추가 계산량	매개변수 변환에 소량의 추가 계산 필요	초기화 후 학습 전 과정 반복
모델 출력 유지 여부	입력-출력 관계 유지	초기 상태에서 성능 보장 불가
목표	해석성 향상 및 퇴행성 제거	성능 향상 또는 새로운 목적 달성

결론

Interaction Basis는 학습된 모델을 재구성하는 과정이지, 모델을 다시 학습해야 하는 것을 의미하지 않습니다. 입력-출력 관계는 그대로 유지되며, 재구성을 통해 해석 가능성과 추론 효율성을 높이는 것이 주요 목적입니다.

학습 중에 적용하려는 경우 추가 고려가 필요하지만, 대부분은 훈련 후 적용하며 기존 성능을 유지합니다. 추가적인 질문이 있다면 언제든 말씀해주세요!

그럼 이제 논문을 기반으로 한번 쭉 정리해줘