https://transformer-circuits.pub/2022/toy_model/
Toy Models of Superposition
It would be very convenient if the individual neurons of artificial neural networks corresponded to cleanly interpretable features of the input. For example, in an “ideal” ImageNet classifier, each neuron would fire only in the presence of a specific v
transformer-circuits.pub
제가 원했던 분야 중 하나입니다.
드디어 조금씩 진행하게 되었네요
일부 뉴런은 명확하게 특징과 매핑된다.
그러나 이 현상은 매우 드물고, LLM에선 더 드물다!
sparse input을 통해 훈련된 작은 ReLU 모델을 통해 모델이 더 많은 피쳐를 표현하는 법을 조사!
superposition - feature가 sparse 할 때 비선형의 interference을 cost로 선형모델이 하는 것 이상의 압축을 허용
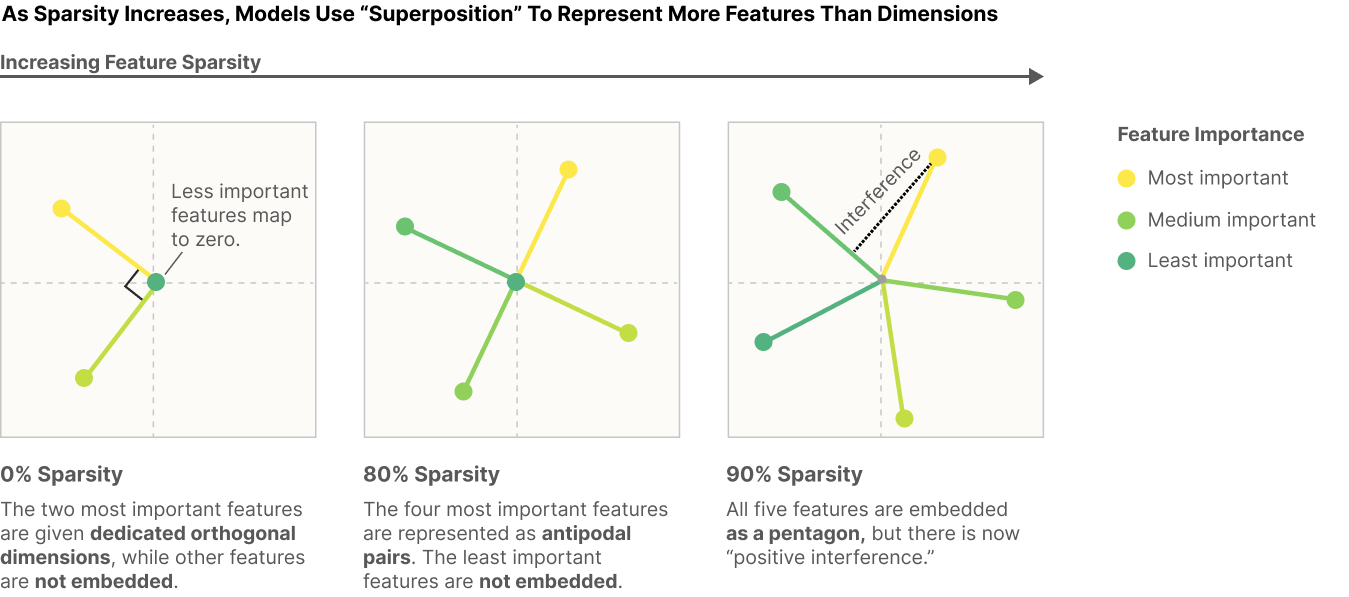
여기서 말하는 중첩(superposition)은, 신경망의 뉴런 하나가 여러 입력 특성(feature)을 동시에 표현하는 현상을 뜻합니다. 이를 통해 신경망이 가지고 있는 차원의 한계를 넘어서 더 많은 정보를 압축하여 저장할 수 있다는 의미로 사용됩니다.
쉽게 말해, 중첩(superposition)은 특정 뉴런이 한 가지 특성에만 대응하지 않고, 여러 특성을 동시에 담는다는 것을 의미해요. 이는 모델이 차원의 제약을 극복하고 더 많은 정보를 처리할 수 있도록 돕지만, 이 과정에서 약간의 간섭(interference)이 발생할 수 있습니다.
비유를 통한 설명
- 예를 들어, 이상적인 상황에서는 하나의 뉴런이 "빨간색"에만 반응하고, 다른 뉴런이 "강아지의 코"에만 반응한다고 가정해 볼 수 있습니다. 이렇게 각 뉴런이 하나의 특성에만 대응하면 해석이 매우 쉬워지죠.
- 그러나 실제 신경망에서는 이런 일이 항상 일어나지 않습니다. 대신에 하나의 뉴런이 "빨간색"뿐만 아니라 "강아지의 코"에도 반응할 수 있습니다. 이렇게 한 뉴런이 여러 특성을 겹쳐서 표현하는 것이 중첩(superposition)입니다.
왜 중첩이 발생할까?
중첩이 발생하는 이유는 신경망이 여러 입력 특성을 압축해서 처리하기 때문입니다. 신경망이 입력 특성의 희소성(sparsity)을 활용해 차원이 부족할 때 여러 특성을 함께 담는 방식으로 더 많은 정보를 저장하려고 하기 때문이죠. 이 과정에서 일종의 압축(효율성)을 달성하지만, 그 대가로 뉴런들이 여러 특성에 걸쳐서 작동하게 되고, 특성이 명확하게 구분되지 않을 수 있습니다. 이것이 "간섭"을 일으킬 수 있는데, 여기서 간섭은 여러 특성이 하나의 뉴런에 동시에 얽혀 제대로 분리되지 못하는 상황을 말해요.
예시를 통한 설명
- 예를 들어, 당신이 두 개의 중요한 특성만 필요로 하는 데이터를 학습시키면, 모델은 두 개의 뉴런만 사용해 이 두 특성을 표현할 수 있습니다.
- 하지만 특성이 더 많아지고 모델의 뉴런이 제한적일 때, 모델은 뉴런 하나에 여러 특성을 압축해서 담기 시작합니다. 이런 상황에서 뉴런은 "강아지의 코"와 "빨간색" 같은 여러 특성에 동시에 반응하게 됩니다. 이렇게 하면 신경망이 더 많은 정보를 표현할 수 있지만, 각 특성이 완벽하게 분리되지 않아 해석이 어려워질 수 있죠.
결국, 중첩은 신경망이 차원을 초과하는 정보를 저장하려는 방식이고, 이는 압축 및 효율성 측면에서 유리하지만 해석 가능한 개별 뉴런의 특성은 희석됩니다.
이 부분에서는 해석 가능성(interpretability) 연구자들에게 중요한 기여를 설명하고 있어요. 핵심은 신경망에서 중첩(superposition)이 실제로 자연스러운 환경에서도 발생한다는 것을 직접 보여준다는 것입니다.
쉽게 풀어서 설명하면:
- 중첩이 실제로 일어난다:
- 연구자들이 말하는 중요한 기여는, 신경망에서 중첩이 단순히 사후 해석(post-hoc interpretation), 즉 사후에 의미를 부여하는 해석이 아니라, 모델의 실제 본질(ground truth)에서 일어난다는 것을 보여주는 거예요. 즉, 신경망이 여러 특성을 한 뉴런에 압축해서 담는 현상은 이론적인 것이 아니라 실제로도 일어난다는 것이죠.
- 이 말은 신경망 자체가 원래부터 여러 특성을 중첩하여 저장하도록 설계된 것처럼 행동한다는 것을 뜻해요. 단순히 "이런 식으로 해석할 수 있겠다"라는 수준이 아니라, 신경망의 구조 속에서 중첩이 본질적인 역할을 하고 있다는 거죠.
- 희소 구조와 중첩:
- 저자들은 신경망이 희소한 구조, 즉 특정 특성이 적거나 일정하지 않은 상황에서도 중첩(superposition)이 자연스럽게 발생한다고 말합니다. 이는 신경망이 특성을 효율적으로 압축하고 처리하는 방식이라는 걸 보여줍니다.
- 단일 의미(monosemantic)와 다중 의미(polysemantic):
- 일부 뉴런은 monosemantic, 즉 하나의 특정 특성에만 반응합니다. 예를 들어, 강아지의 코에만 반응하는 뉴런이 있을 수 있죠.
- 반면, polysemantic 뉴런은 여러 가지 관련 없는 특성에 동시에 반응할 수 있습니다. 예를 들어, 강아지의 코와 빨간색에 모두 반응하는 뉴런이 있을 수 있어요.
- 이 연구는 이러한 차이가 왜 생기고 어떻게 발생하는지를 설명하려고 합니다.
- 복잡한 기하학적 구조:
- 연구자들은 실험한 장난감 모델(toy model)에서 중첩이 복잡한 기하학적 구조를 보인다고 발견했습니다. 이는 중첩 현상이 단순히 특성들이 겹치는 것 이상으로, 신경망 내부에서 특성들이 어떻게 배열되고 있는지에 대한 더 깊은 구조적 의미를 암시합니다.
결론적으로:
이 연구는 신경망이 여러 특성을 겹쳐서 저장하는 현상이 실제로 일어나는 자연스러운 현상임을 시연하고, 이로 인해 뉴런들이 때로는 하나의 특성에 반응하고, 때로는 여러 특성에 동시에 반응하는 이유를 설명하려고 합니다. 그리고 이 중첩이 단순한 이론이 아니라, 신경망의 실제 구조와 관련이 있다는 점을 보여주려고 합니다.
Definitions and Motivation - Features, Directions and Superposition
linear representation hypothesis
Decomposability : 네트워크 표현은 독립적으로 이해 가능한 특징들로 설명될 수 있다.
전체를 생각하지 않아도 모델에 대해 추론할 수 있어야 한다.
이것 만으로는 충분하지 않고, individual features를 identify해야한다! - Linear representation
Linearity : 특징은 방향으로 표현될 수 있다.
우리는 왜 때때로 유용한 feature를 확인하지만 어떨때는 못 할까?
Privileged Basis : 일부 표현만이 뉴런과 대응하도록 특권(Priviledge Basis)를 가진다.
Superposition : 중첩(Superposition)을 통해 차원보다 더 많은 feature를 표현할 수 있다.
Neural networks가 더 큰 networks를 시뮬레이션 하는 것 처럼 보인다.
이 부분은 신경망의 해석 가능성(interpretability)을 연구하는 과정에서 특성(features)이 어떻게 신경망의 활성화 공간(activation space)에서 방향(directions)으로 표현될 수 있는지에 대한 개념을 다루고 있습니다. 핵심 아이디어는 신경망 내부의 표현(representation)을 이해하고 분해할 수 있는 방법에 대한 것입니다.
주요 개념 및 동기 설명:
1. 특성(features)과 방향(directions):
- 연구에서는 신경망이 입력된 데이터를 처리할 때 특성들이 활성화 공간에서 방향(directions)으로 표현된다고 가정합니다. 여기서 "방향"은 수학적으로 벡터를 의미하며, 신경망의 활성화 값(activation)을 특정한 방식으로 설명할 수 있는 벡터 공간의 방향을 나타냅니다.
- 예를 들어, 워드 임베딩(word embeddings)에서 "성별 방향(gender direction)"이라는 표현을 사용할 때, 이는 신경망이 성별 정보를 특정한 방향(벡터)으로 표현하고 있다는 가정입니다. 마찬가지로, 비전 모델(vision models)에서 "곡선 탐지 뉴런(curve detector neurons)"을 이야기할 때도 이는 신경망이 시각적 특성을 특정 방향으로 표현하고 있다는 가정을 내포합니다.
- 이 가정은 신경망이 데이터를 처리하는 구조에 대해 강력한 주장을 하고 있는데, 신경망이 입력 특성을 선형적 방향으로 나타낼 수 있다는 것입니다.
2. Decomposability (분해 가능성):
- Decomposability는 신경망의 표현을 독립적으로 이해 가능한 특성들로 분해할 수 있다는 것입니다. 즉, 모델이 어떻게 입력 데이터를 처리하는지 이해하려면 신경망의 표현을 쉽게 나누어서 각 특성들이 독립적으로 어떤 역할을 하는지 설명할 수 있어야 합니다.
- 이 개념은 신경망을 해석할 때 매우 중요합니다. 우리가 신경망을 역공학(reverse engineering)하려면, 각 뉴런이나 레이어가 어떤 정보를 표현하는지 전체 구조를 머릿속에 다 담지 않고도 이해할 수 있어야 하죠. 이때 분해 가능성이 필수적입니다.
3. Linearity (선형성):
- Linearity는 신경망이 입력된 데이터를 선형적으로 표현할 수 있다는 가정입니다. 즉, 각 특성이 활성화 공간에서 특정한 방향으로 표현된다는 의미입니다. 이를 통해 각 특성이 특정 벡터 방향에 대응하게 되고, 이를 통해 그 특성의 표현을 이해할 수 있게 됩니다.
- 선형성은 신경망을 해석할 때 중요한 속성입니다. 선형적 표현을 통해, 특정한 방향이 어떤 입력 특성에 대응하는지 확인할 수 있고, 이를 기반으로 해석 가능한 신경망을 만들 수 있습니다.
4. Privileged Basis (특권적인 기저):
- Privileged Basis는 특정한 신경망 표현들이 특정 기저 벡터(basis vectors)와 잘 맞아떨어지는 상황을 설명합니다. 즉, 뉴런들이 특성들과 정렬되어 있는 경우입니다. 이 경우, 특정 뉴런이 특정 특성에 반응하여 신경망을 해석하기가 더 쉬워집니다.
- 예를 들어, InceptionV1 같은 초기 층에서는 특정 뉴런들이 곡선 탐지 뉴런처럼 특정한 특성에만 반응하는 경우가 많이 관찰되는데, 이런 경우가 바로 Privileged Basis 상황입니다.
5. Superposition (중첩):
- Superposition은 신경망이 하나의 방향에 여러 특성들을 압축하여 표현하는 방식입니다. 즉, 신경망이 가진 차원보다 더 많은 특성을 표현할 수 있게 해주는 전략으로, 특성들이 서로 겹쳐져서 하나의 뉴런이 여러 특성에 동시에 반응할 수 있게 만듭니다.
- 이 현상은 신경망이 더 큰 신경망을 시뮬레이션하는 것처럼 작동하게 만듭니다. 이는 특성이 더 많이 압축되어 표현되기 때문에, 특성들이 뉴런에 직접 대응되지 않는 경우가 발생합니다.
6. 연구의 목표:
- 이 연구의 목표는 Superposition이 실제로 신경망에서 발생하는 것을 명확히 보여주고, 이것이 어떻게 Privileged Basis와 상호작용하는지를 탐구하는 것입니다. 이는 해석 가능성 연구에서 매우 중요한 개념입니다. 만약 신경망에서 중첩이 일어난다면, 우리가 신경망을 해석하는 방식 자체가 달라질 수 있습니다.
결론:
이 섹션은 특성, 방향, 중첩 개념을 통해 신경망의 내부 표현을 해석하는 방법을 설명하려고 합니다. 특히, 신경망이 특성들을 선형적인 방향으로 표현하고, 이를 분해할 수 있는지, 그리고 중첩이 발생할 때 해석 가능성에 어떤 영향을 미치는지를 다루고 있습니다.
그런데 여기서 말하는 활성화 값이랑 활성화 공간이 뭐야?
활성화 값(activation value)과 활성화 공간(activation space)은 신경망의 작동 원리를 이해하는 데 중요한 개념입니다. 이 두 용어는 신경망이 데이터를 처리하는 방식을 설명할 때 자주 사용됩니다. 차례대로 설명해 드릴게요.
1. 활성화 값(activation value)
- 정의: 활성화 값은 신경망의 각 뉴런이 입력을 처리한 후 출력하는 값입니다. 뉴런은 입력을 받아 가중치(weight)와 바이어스(bias)를 적용한 후, 활성화 함수(예: ReLU, sigmoid, tanh 등)를 통과시켜 활성화 값을 계산합니다.
- 역할: 활성화 값은 신경망의 각 층(layer)에서 뉴런이 얼마나 "활성화"되는지, 즉 특정 입력에 얼마나 반응하는지를 나타냅니다.
- 예를 들어, 이미지 분류 모델에서는 "고양이의 귀" 같은 특성이 있을 때, 특정 뉴런이 활성화되어 그 특성에 강하게 반응할 수 있습니다. 그 뉴런의 출력 값(활성화 값)은 높아지고, 다른 특성에 반응하는 뉴런들은 낮은 활성화 값을 가질 수 있죠.
- 뉴런의 반응: 이 활성화 값은 각 뉴런이 입력 데이터를 보고 얼마나 반응하는지를 수치로 나타낸 것이라고 볼 수 있습니다. 값이 클수록 그 뉴런이 해당 특성에 강하게 반응하고 있다는 의미입니다.
2. 활성화 공간(activation space)
- 정의: 활성화 공간은 신경망에서 한 층 전체의 뉴런들이 출력한 활성화 값들의 벡터 공간을 의미합니다. 즉, 입력 데이터가 신경망을 통과하면서 각 층에서 생성된 모든 뉴런들의 활성화 값이 모여 형성된 공간입니다.
- 벡터 공간으로 이해: 활성화 공간은 수학적으로 벡터 공간으로 표현될 수 있습니다. 예를 들어, 만약 특정 층에 100개의 뉴런이 있다면, 그 층에서 하나의 입력이 처리될 때 나오는 100개의 활성화 값이 하나의 벡터가 됩니다. 이렇게 입력마다 각 층에서 새로운 벡터가 생성되면서, 여러 벡터들로 구성된 활성화 공간이 만들어지는 것입니다.
- 특성의 방향: 이 공간에서 각 특성은 특정 방향으로 표현됩니다. 신경망이 입력 데이터를 처리하면서 입력의 특정 특성(예: 고양이의 귀, 빨간색 등)이 활성화 공간의 어떤 방향(벡터)에 대응하게 됩니다. 이를 통해 신경망은 입력 데이터를 선형적으로 혹은 비선형적으로 분해해서 다루게 되는 것입니다.
활성화 값과 활성화 공간의 관계
- 활성화 값은 개별 뉴런의 출력 값이고, 이 값들이 모여서 층 전체의 출력을 형성합니다. 이러한 출력이 활성화 공간을 이루며, 신경망이 입력을 처리하면서 생성되는 다차원적인 벡터 공간을 형성합니다.
- 신경망의 각 층에서 입력 데이터를 어떻게 표현하는지는 이 활성화 공간 내에서 벡터로 나타나며, 신경망의 해석 가능성 연구에서 중요한 역할을 합니다. 예를 들어, "성별"이라는 특성이 활성화 공간 내에서 하나의 벡터 방향(성별 방향)으로 나타날 수 있습니다. 특정 뉴런들이 이 방향을 강하게 활성화한다면, 해당 뉴런들은 성별 정보를 인식하고 처리한다고 볼 수 있죠.
요약
- 활성화 값: 신경망의 각 뉴런이 특정 입력에 대해 계산한 출력 값.
- 활성화 공간: 신경망의 특정 층에서 모든 뉴런들이 생성한 활성화 값들이 구성하는 다차원 벡터 공간.
이 개념을 바탕으로 신경망이 입력 데이터를 처리하고 해석하는 방식을 이해할 수 있습니다.
Word embeddings - 의미적 속성에 따라 방향을 가진다
ex) V("queen") = V("king") - V("man") + V("woman")
Latent spaces - 유사한 백터 연산과 해석가능한 방향 결과
Interpretable Neurons - (CNN, RNN, GAN)해석 가능한 것으로 보이는 뉴런 찾기에 결과가 있었다. 그러나 몇가지 특정 뉴런에 대해서 였고, 이해할 수 있는 특징을 실제로 감지하는 뉴런에 대해 확실히 하려고 한다.
Universality - 동일한 속성에 반응하는 여러 뉴런들이 네트워크 전반에 퍼져있다.
Polysemantic Neurons - 관련 없는 속성에도 반응하는 다의미적 뉴런이 많이 있다.
What are Features?
Features - 뉴런이 반응하는 것을 관찰하는 모든 해석가능한 속성
임의의 함수로서의 Features - 함수로 정의하면 모델 전체적으로 확인하여 특징 각각을 보기 보단 혼합물로 확인된다.
해석 가능한 속성으로서의 Features - 우리가 이해하지 못하는 Features도 허용해 줘야 복잡한 모델에서도 우리가 추후에 이해할 수 있다.
충분히 큰 모델의 뉴런 - 곡선 감지기와 같은 경향이다.
이 부분은 "특성(feature)"의 정의를 설명하는 내용입니다. 여기서는 "특성"이란 무엇인지 명확히 정의하는 것이 매우 어렵다는 점을 이야기하며, 세 가지 잠재적인 정의를 제안하고 있습니다. 이 설명을 통해 특성이 무엇을 의미하는지에 대해 보다 깊이 이해할 수 있습니다.
1. 특성(feature)의 개념
- 특성(feature)이란 신경망이 입력 데이터에서 반응하거나 감지하는 해석 가능한 속성입니다. 예를 들어, 이미지 인식 모델에서는 "고양이"나 "자동차" 같은 개념이 특성으로 작동할 수 있고, 언어 모델에서는 "성별", "감정" 같은 정보가 특성이 될 수 있습니다.
- 하지만 특성을 명확하게 정의하는 것은 복잡합니다. 단순히 데이터에 어떤 함수가 적용된 결과를 특성이라고 하기에는 충분하지 않다는 것이 이 부분의 핵심 논점입니다. 특성은 더 추상적이고 해석 가능한 속성으로 보이며, 이 추상적 속성을 이해하고 설명하는 여러 정의를 고민해 봅니다.
2. 세 가지 특성 정의:
1) 특성 = 임의의 함수:
- 첫 번째 정의는 특성을 입력 데이터에 대한 임의의 함수로 보는 것입니다.
- 즉, 입력 데이터에 어떤 함수가 적용되든 그것이 출력값을 만들면 특성이라고 할 수 있습니다.
- 하지만 이 정의는 연구자들의 동기에 맞지 않습니다. 그 이유는 특성이 단순한 함수 이상의 중요한 추상적 개념이어야 한다고 여기기 때문입니다. 예를 들어, "고양이"나 "자동차" 같은 특성은 여러 모델에서 일관되게 나타나는 근본적인 추상적 개념으로 보이며, 임의의 함수보다 더 의미 있는 구조를 가지고 있습니다.
2) 특성 = 해석 가능한 속성:
- 두 번째 정의는 특성을 인간이 이해할 수 있는 속성으로 보는 것입니다.
- 예를 들어, "고양이", "자동차" 같은 인간이 쉽게 이해할 수 있는 개념(concepts)을 특성으로 정의합니다.
- 하지만 이 정의에도 문제가 있습니다. 신경망이 발견할 수 있는 특성 중에는 인간이 이해하기 어려운 복잡한 패턴도 존재할 수 있기 때문입니다. 예를 들어, AlphaFold 같은 모델이 단백질 접힘을 예측하는 데 중요한 화학적 구조를 발견할 수 있는데, 인간이 처음에는 이것을 이해하지 못할 수도 있습니다. 따라서 인간의 이해를 기반으로 한 정의는 제한적일 수 있습니다.
3) 특성 = 충분히 큰 모델에서 나타나는 뉴런의 속성:
- 세 번째 정의는 특성을 충분히 큰 신경망이 입력 데이터를 처리하면서 특정 뉴런에 안정적으로 할당하는 속성으로 보는 것입니다.
- 예를 들어, 시각 모델에서 곡선 탐지 뉴런이 자주 나타나는 것을 특성으로 정의할 수 있습니다. 큰 모델에서는 안정적으로 특정 뉴런들이 특정한 특성을 감지하게 되고, 이것을 특성이라고 부르는 것입니다.
- 이 정의는 약간 순환적인(circular) 정의일 수 있지만, 다른 정의들의 문제를 피할 수 있습니다. 즉, 특정 뉴런이 어떤 특성에 반응할 때 이를 특성으로 간주하는 방식으로 정의하는 것입니다.
3. 결론 및 유연성:
- 이 논문에서는 세 번째 정의(특성 = 충분히 큰 모델에서 나타나는 뉴런의 속성)에 따라 작업하고 있지만, 이 정의에 과도하게 얽매이지 않으려 한다고 언급합니다.
- 연구가 진행됨에 따라 특성의 정의가 더 명확해질 수 있기 때문에, 아직은 하나의 정의에 고정되지 않는 것이 중요하다고 강조하고 있습니다.
요약:
이 섹션에서는 특성(feature)의 정의에 대해 여러 가지 가능성을 논의합니다. 특성을 단순한 함수로 정의하는 것보다, 신경망이 일관되게 감지하는 추상적 속성이 중요하며, 이는 충분히 큰 신경망에서 특정 뉴런이 안정적으로 반응하는 속성으로 볼 수 있습니다.
Features as Directions
단어 임베딩에서 본 것과 마찬가지로 Feature는 Direction으로 표현된다.
표현되는 feature는 입력의 비선형 함수다!
선형 표현 - feature와 weight의 곱 -> 선형적으로 접근 가능해주게 하고, 통계적으로 효율적이다.
선형 표현도 레이어를 쌓으면 비선형적으로 표현을 구현한다.
선형 표현에서 차원 만큼만 피쳐를 저장할 수 있는 것이 아니라 중첩을 통해 더 많은 feature를 저장할 수 있다.
이 부분은 특성(features)이 신경망에서 어떻게 방향(directions)으로 표현되는지에 대한 설명입니다. 특히, 선형 표현(linear representation)을 통해 신경망이 데이터를 처리하고 특성을 저장하는 방식에 초점을 맞추고 있습니다. 또한, 선형 표현의 장점과 한계를 설명하며, 중첩(superposition) 현상이 어떻게 더 많은 특성을 선형 공간에 저장할 수 있게 하는지도 다룹니다.
1. 특성 = 방향(directions)
- 특성(features)을 방향으로 표현: 신경망에서 입력 데이터를 처리할 때, 특성은 활성화 공간(activation space)에서 특정한 방향(벡터)으로 표현됩니다. 예를 들어, 워드 임베딩(word embeddings)에서는 "성별(gender)"이나 "왕족(royalty)" 같은 특성이 벡터 방향으로 표현되어, 벡터 산술 연산이 가능해집니다. 유명한 예시로는, V("king") - V("man") + V("woman") = V("queen")과 같은 방식으로 성별과 관련된 정보를 벡터 차원에서 조작할 수 있습니다.
- 해석 가능한 뉴런: 신경망에서 해석 가능한 뉴런도 이와 비슷한 방식으로 작동합니다. 뉴런의 활성화 값이 활성화 공간에서 특정한 기저 방향(basis direction)에 대응하게 됩니다. 즉, 뉴런이 특정 특성에 반응할 때, 그 특성은 특정 방향으로 표현됩니다.
2. 선형 표현(linear representation)
- 선형 표현의 정의: 신경망이 선형 표현을 가진다고 할 때, 이는 각 특성 f_i가 활성화 공간에서 특정한 방향 W_i로 표현된다는 뜻입니다. 여러 특성들이 함께 활성화될 경우, 그 활성화 값은 이 방향들의 선형 결합으로 나타납니다:
xf1Wf1+xf2Wf2+⋯여기서 x_{f1}, x_{f2}는 각각의 특성 값이고, W_{f1}, W_{f2}는 해당 특성에 대응하는 벡터 방향입니다. - 비선형 특성과의 관계: 중요한 점은, 특성 자체는 입력 데이터의 비선형 함수일 수 있지만, 그 특성을 활성화 벡터 공간에 표현하는 방식은 선형적이라는 겁니다. 즉, 신경망이 특성을 어떻게 입력 데이터로부터 추출하느냐는 비선형적일 수 있지만, 이 특성이 활성화 공간에서 표현되는 방식은 선형적입니다.
3. 선형 표현의 이점
연구자들은 선형 표현이 신경망에서 자연스럽게 발생하는 현상이며, 이에 몇 가지 중요한 장점이 있다고 설명합니다.
1) 패턴 매칭의 용이함:
- 뉴런이 특정한 가중치(weight) 패턴에 따라 패턴 매칭을 수행할 때, 입력 자극이 패턴과 잘 맞으면 뉴런이 더 많이 활성화되고, 덜 맞으면 덜 활성화됩니다. 이는 선형적인 표현 방식을 따릅니다.
2) 선형적 접근성(linear accessibility):
- 선형 표현이 있으면, 신경망의 다음 층에서 특성을 쉽게 선택할 수 있습니다. 예를 들어, 이전 층에서 어떤 특성이 선형적으로 표현되었다면, 다음 층의 뉴런은 이 특성을 쉽게 감지하고 활성화하거나 억제할 수 있습니다. 비선형적으로 표현된 특성은 이런 간단한 방식으로 접근할 수 없기 때문에, 선형 표현이 더 효율적입니다.
3) 통계적 효율성(statistical efficiency):
- 선형 표현은 비선형 표현보다 일반화 능력이 더 뛰어날 수 있습니다. 즉, 선형 표현을 통해 모델이 더 쉽게 비국소적(non-local)으로 일반화할 수 있어, 통계적으로 더 효율적인 학습을 가능하게 합니다. 이는 신경망이 데이터를 더 잘 일반화하고 새로운 상황에서 성능을 발휘할 수 있도록 도와줍니다.
4. 비선형 표현 vs 선형 표현
- 비선형 표현도 가능하지만, 이들은 대개 더 복잡하며 신경망이 정보를 효율적으로 처리하는 데 적합하지 않다고 설명합니다. 실제로 신경망에서 비선형 표현을 사용하려면 여러 층(layer)을 거쳐야 하며, 이는 복잡성을 증가시킵니다. 따라서 선형 표현이 더 간단하고 효율적입니다.
5. 중첩(superposition)과 선형 표현
- 중첩(superposition)은 선형 표현을 사용하는 신경망이 더 많은 특성을 저장할 수 있게 해주는 현상입니다. 일반적으로는 선형 표현이 가질 수 있는 특성의 수가 공간의 차원에 의해 제한되지만, 중첩을 사용하면 신경망이 차원 수보다 더 많은 특성을 저장할 수 있습니다. 이는 선형 표현에서도 여러 특성을 겹쳐서 저장할 수 있음을 의미하며, 신경망이 더 효율적으로 특성을 관리할 수 있게 해줍니다.
요약
이 섹션은 신경망에서 특성을 선형적인 방향으로 표현하는 방식을 설명하고 있습니다. 신경망이 선형 표현을 사용하면, 패턴 매칭이 쉽고 특성을 효율적으로 접근할 수 있으며, 통계적으로 더 좋은 일반화 능력을 가질 수 있습니다. 중첩을 통해 선형 표현 내에서 더 많은 특성을 저장하는 것도 가능하며, 이는 신경망의 효율성을 높이는 중요한 전략입니다.
여기서 선형적이다 라는 것은 어떤 의미야???
선형 표현쪽이 잘 이해가 안가네
여기서 말하는 "선형적이다"는 선형 대수학의 개념을 기반으로 신경망에서 특성(features)을 특정한 방식으로 표현하고 처리하는 방법을 의미합니다. 이 개념은 신경망이 입력 데이터를 처리할 때, 각 특성이 활성화 공간(activation space)에서 직선적인 관계, 즉 벡터 공간에서의 방향으로 나타난다는 것을 설명하는 데 사용됩니다. 이제 선형성의 의미를 좀 더 구체적으로 설명해 볼게요.
1. 선형적 표현이란?
- 선형적이다는 수학적으로 입력과 출력이 비례하는 관계를 말합니다. 예를 들어, 어떤 함수 f(x)가 선형적이라면, 다음과 같은 성질을 가집니다:
- f(a * x) = a * f(x): 입력에 상수를 곱하면 출력도 그 상수만큼 커집니다.
- f(x + y) = f(x) + f(y): 입력을 더하면 출력도 더해집니다.
이러한 선형적 관계를 신경망에서 특성을 표현하는 방식으로 이해할 수 있습니다. 신경망이 입력 데이터를 처리할 때, 그 데이터 속의 각 특성은 활성화 공간에서 특정한 방향(벡터)으로 표현되며, 이 특성들이 결합하는 방식이 선형 결합을 따릅니다.
2. 신경망에서의 선형 표현
- 신경망의 활성화 공간(activation space)은 각 뉴런의 출력 값을 벡터로 나타내는 공간입니다. 이 공간에서 각 특성은 특정한 방향(direction)으로 표현됩니다. 예를 들어, "고양이"라는 특성은 활성화 공간에서 하나의 벡터 방향으로 나타나고, "개"라는 특성도 또 다른 방향으로 나타납니다.
- 선형 표현이란, 신경망이 각 특성을 이렇게 벡터 방향으로 나타내고, 이 벡터들이 선형 결합(linear combination) 형태로 결합되어 여러 특성이 함께 표현되는 방식입니다. 이는 다음과 같이 수식으로 나타낼 수 있습니다
:xf1Wf1+xf2Wf2+⋯여기서:- x_{f1}, x_{f2}는 각 특성의 활성화 값을 의미합니다. 즉, 해당 특성이 얼마나 강하게 나타나는지를 나타내는 값입니다.
- W_{f1}, W_{f2}는 각 특성의 벡터 방향입니다. 특성이 활성화 공간에서 나타나는 방향을 나타냅니다.
3. 선형 표현의 장점
선형 표현이 신경망에서 중요한 이유는, 이를 통해 특성을 쉽게 처리하고, 해석할 수 있기 때문입니다. 다음은 선형 표현이 가진 주요 장점입니다:
1) 간단한 패턴 매칭:
- 뉴런이 입력에 대해 특정 패턴을 감지하고 싶을 때, 선형적으로 설정된 뉴런은 입력이 그 패턴과 잘 맞을수록 더 강하게 반응하고, 그렇지 않으면 덜 반응하게 됩니다. 이는 뉴런이 입력과 선형적인 관계를 가지며 작동하기 때문에 가능한 일입니다.
2) 선형적 접근성:
- 선형 표현 덕분에, 다음 층의 뉴런이 이전 층의 특정 특성을 쉽게 선택하고 활성화할 수 있습니다. 선형적으로 표현된 특성은 한 단계에서 쉽게 선택될 수 있는데, 이는 비선형적으로 표현된 특성에서는 어렵습니다. 예를 들어, 한 뉴런이 "고양이" 특성에만 반응하도록 훈련되면, 그 특성은 특정 방향으로 표현되고, 다음 층에서 그 방향을 손쉽게 추출할 수 있습니다.
3) 통계적 효율성:
- 선형 표현을 사용하면 신경망이 비선형 모델보다 데이터를 더 효율적으로 일반화할 수 있습니다. 즉, 새로운 데이터에 대한 예측을 할 때 일반화 성능이 더 높을 수 있습니다. 비선형 표현은 더 많은 층과 복잡한 연산이 필요하지만, 선형 표현은 그보다 간단하게 더 많은 특성을 처리할 수 있습니다.
4. 비선형 표현과의 차이점
- 비선형 표현은 각 특성이 독립적으로 선형적인 방향으로 표현되지 않고, 복잡하게 얽혀서 표현됩니다. 이를 처리하려면 여러 층(layer)을 거쳐야 하고, 복잡한 연산이 필요합니다.
- 반면, 선형 표현은 하나의 층에서 여러 특성을 선형적으로 결합할 수 있기 때문에, 더 간단하고 효율적인 방식입니다.
5. 중첩(superposition)과 선형 표현
보통 선형 표현은 활성화 공간의 차원 수에 따라 저장할 수 있는 특성의 수가 제한됩니다. 하지만 중첩(superposition)이라는 현상을 통해, 신경망은 선형 공간 내에서 더 많은 특성을 겹쳐서 저장할 수 있습니다. 이는 신경망이 차원 수보다 더 많은 특성을 처리할 수 있도록 도와주는 중요한 전략입니다.
결론:
"선형적이다"는 신경망이 입력 데이터를 처리할 때 특성들을 벡터 방향으로 표현하고, 그 특성들이 선형적으로 결합되어 처리되는 방식을 의미합니다. 선형 표현 덕분에 신경망은 각 특성을 쉽게 처리하고, 해석 가능한 방식으로 데이터를 이해할 수 있습니다.
그럼 여기서 xf1은 특정 레이어에서 1번 노드의 출력이겠지?
그럼 wf1은 어떻게 나오는거야?
이게 잘 이해가 안가네
네, 맞습니다. 여기서 x_{f1}은 특정 레이어에서 1번 노드의 출력값(활성화 값)을 의미합니다. 즉, 입력이 주어졌을 때, 그 입력에 대해 1번 노드가 얼마나 활성화되었는지를 나타내는 값이죠. 이제 W_{f1}에 대해 설명하겠습니다.
W_{f1}은 무엇인가?
W_{f1}은 1번 특성에 대응하는 벡터 방향입니다. 즉, 입력 데이터를 처리하는 신경망의 활성화 공간(activation space)에서 특정 특성(예: 성별, 감정, 물체의 곡선)을 표현하는 방향을 나타냅니다. 이 벡터는 신경망이 학습을 통해 결정하게 됩니다.
1. W_{f1}은 학습된 가중치 벡터:
- 신경망에서 각 노드는 가중치(weight)를 가지고 있으며, 입력 데이터는 이 가중치들과 곱해져서 출력 값(활성화 값)을 만듭니다. 이때 W_{f1}은 특정 특성에 대한 가중치 벡터입니다.
- 예를 들어, 신경망이 "고양이"라는 특성을 학습한다면, 이 특성에 대응하는 벡터인 W_{f1}은 신경망이 고양이를 인식할 수 있는 방향을 나타내는 가중치 벡터로 학습됩니다. 입력 데이터가 이 벡터와 잘 맞으면(W_{f1}과의 내적 결과가 크면), 그 특성에 강하게 반응하게 됩니다.
2. 벡터 방향과 특성의 대응:
- 신경망의 활성화 공간에서 각 특성은 벡터 방향으로 나타납니다. W_{f1}은 이 특성에 대응하는 벡터 방향입니다. 예를 들어, 신경망이 "성별"이라는 특성을 학습하면, W_{f1}은 성별과 관련된 정보를 인식하는 벡터 방향을 나타냅니다.
- W_{f1}은 벡터이기 때문에, 여러 차원의 값으로 이루어져 있으며, 이 벡터는 신경망의 학습 과정을 통해 결정됩니다. 신경망이 다양한 데이터를 학습하면서 "이 특성에 반응하기 위해서는 이런 방향으로 데이터를 해석해야 한다"는 것을 학습하는 것이죠.
3. W_{f1}과 x_{f1}의 곱:
- x_{f1}은 그 특성에 대한 활성화 값으로, 입력 데이터가 그 특성에 얼마나 부합하는지를 나타냅니다. 이 값이 클수록 입력 데이터가 그 특성과 잘 맞는다는 의미입니다.
- W_{f1}은 해당 특성에 대응하는 벡터 방향입니다. 따라서, x_{f1} * W_{f1}은 그 특성이 활성화 공간 내에서 어떤 방식으로 표현되는지를 나타냅니다. 즉, 특성에 대응하는 방향으로 얼마만큼의 강도로 반응할지를 결정하는 역할을 합니다.
W_{f1}의 학습 과정
- 초기 가중치 설정: 처음 신경망을 학습할 때, 가중치 벡터 W_{f1}은 무작위로 초기화됩니다. 신경망은 주어진 데이터를 기반으로 가중치를 업데이트하면서 학습합니다.
- 역전파(backpropagation): 신경망은 **손실 함수(loss function)**를 기반으로 출력과 실제 값 간의 차이를 줄이기 위해 가중치를 업데이트합니다. 이를 역전파(backpropagation) 과정이라고 합니다. 이 과정에서 신경망은 입력 데이터와 목표 특성 간의 관계를 학습하고, 각 특성에 대한 **가중치 벡터(W_{f1})**를 조정합니다.
- 가중치 벡터의 학습 결과: 여러 번의 학습을 거치면서 W_{f1}은 특정 특성에 반응하는 방식으로 최적화됩니다. 예를 들어, 신경망이 이미지 데이터를 학습하면서 "고양이"라는 특성에 강하게 반응하도록 가중치 벡터 W_{f1}이 조정됩니다.
요약
- x_{f1}은 특정 레이어에서 1번 노드의 출력 값(특성에 대한 활성화 값)을 의미하며, 입력이 특정 특성에 얼마나 잘 맞는지를 나타냅니다.
- W_{f1}은 1번 특성에 대응하는 벡터 방향으로, 신경망이 학습을 통해 얻은 가중치 벡터입니다. 이는 특정 특성을 인식하고 처리하는 방식에 따라 학습된 벡터입니다.
- x_{f1} * W_{f1}은 그 특성에 얼마나 강하게 반응하는지와 관련된 값을 나타내며, 이는 신경망이 데이터를 해석하고 특성을 표현하는 중요한 메커니즘입니다.
결국 W_{f1}은 신경망이 학습을 통해 결정한 특성에 대응하는 방향이고, x_{f1}은 그 특성이 얼마나 강하게 나타나는지를 나타내는 활성화 값입니다.
->W는 weight Vector로 다음 layer에 feature를 각각 가중치 만큼 전달해준다.
Privileged vs Non-privileged Bases
단어 임베딩에서 bias direction(기저 방향 - 차원 축)을 분석하는 것은 의미 없다. - Non-Privileged Bases
activation function을 통해 대칭성을 깨고 방향을 특별하게 만들어 feature가 기본 차원과 일치하도록 만든다. - Privileged
Basis directions = Neurons

위 사실을 기반으로 뉴런이 privileged basis에 있을 때만 해석 가능한지 묻는 것이 합리적
이 부분에서는 Privileged Basis(특권적 기저)와 Non-privileged Basis(비특권적 기저)라는 개념을 통해 특성이 신경망에서 어떻게 방향(directions)으로 표현되는지와 어떤 상황에서 이 방향들이 의미를 갖는지를 다루고 있습니다.
1. 기저(basis)란?
- 기저(basis)는 선형 대수에서 벡터 공간의 좌표계를 구성하는 방향들입니다. 벡터 공간에서 임의의 벡터는 기저 벡터의 선형 결합으로 표현됩니다. 예를 들어, 3차원 공간에서는 x축, y축, z축이 기저 역할을 할 수 있습니다.
- 신경망에서 특성(feature)들이 벡터 공간에서 특정한 방향으로 표현될 때, 이 방향들은 어떤 기저와 정렬되어 있을 수 있습니다. 그러나 그 기저가 항상 중요한 것은 아닙니다. 기저가 특권적(Privileged)인지, 아니면 그렇지 않은지에 따라 특성의 해석 가능성이 달라집니다.
2. Privileged Basis vs Non-privileged Basis
이 개념은 신경망에서 특정한 기저가 왜 중요한지를 설명하는 중요한 개념입니다.
1) Non-privileged Basis (비특권적 기저):
- 비특권적 기저란, 특정 방향들이 특별하지 않은 기저입니다. 즉, 모든 방향이 동등한 중요성을 가집니다.
- 예를 들어, 워드 임베딩(word embeddings)에서 사용되는 벡터 공간은 비특권적 기저를 따릅니다. 여기서 각 벡터의 방향은 특정 특성에 고유하게 대응하지 않습니다. 즉, 각 기저 방향(예: x축, y축)이 다른 방향보다 더 중요하거나 해석 가능한 것은 아닙니다.
- 이유: 워드 임베딩에서 특정한 방향이 더 중요하다고 생각할 이유가 없습니다. 모든 방향은 똑같이 중요한 역할을 하며, 특성들은 어떤 임의의 선형 변환을 통해 다른 방향으로 재조정될 수 있습니다. 예를 들어, "man"과 "woman"의 벡터 차이를 사용하여 성별 방향을 정의할 수 있지만, 이 방향은 기저 벡터와 정렬되지 않을 수 있습니다.
- 무작위 선형 변환: 만약 임베딩 공간에 임의의 선형 변환 M을 적용하고, 그에 맞게 가중치에 M⁻¹를 적용하면, 특성들은 여전히 같은 방식으로 표현되지만, 벡터 공간의 기저가 완전히 다르게 변할 수 있습니다. 이는 비특권적 기저의 대표적인 예로, 기저 자체는 해석과 상관없다는 뜻입니다.
2) Privileged Basis (특권적 기저):
- 특권적 기저란, 특정한 기저 방향들이 특별한 의미를 가지는 경우입니다. 이러한 기저에서는 특성들이 특정 방향과 더 정렬되도록 유도됩니다.
- 예를 들어, 신경망의 특정 레이어에서는 활성화 함수(activation function)와 같은 아키텍처적 요소가 대칭을 깨뜨리고, 특정 방향들을 더 중요한 방향으로 만들 수 있습니다. 이는 특성들이 특정 기저 방향에 맞춰져 표현되는 경우입니다. 이때 기저 방향들이 의미를 가지게 되며, 이를 "뉴런"이라고 부를 수 있습니다.
- 뉴런과 해석 가능성: 이런 특권적 기저에서, 신경망의 뉴런들은 종종 해석 가능한 특성과 직접 연결됩니다. 예를 들어, 곡선 탐지 뉴런이나 고양이 얼굴 탐지 뉴런과 같은 해석 가능한 뉴런들이 바로 이런 특권적 기저에 존재할 가능성이 큽니다.
3. 해석 가능성의 차이
- 특권적 기저가 있을 때, 뉴런이 특정 특성을 해석 가능하게 표현할 수 있습니다. 즉, 이 뉴런이 특정한 특성에 맞춰 활성화되며, 이 뉴런의 활성화가 특정 특성을 나타내기 쉽습니다.
- 반대로, 비특권적 기저에서는 특정한 방향이 중요하지 않기 때문에, 뉴런이 특정 특성을 해석 가능하게 표현한다고 보기는 어렵습니다. 워드 임베딩처럼 각 벡터 방향은 임의적이고, 기저와는 상관없이 여러 방향이 섞여서 특성을 표현하게 됩니다.
4. Privileged Basis의 조건
- 특권적 기저가 있다고 해서 항상 특성이 기저 방향과 정렬되는 것은 아닙니다. 특성들이 특권적 기저와 일치하지 않을 수도 있지만, 특권적 기저가 있어야 해석 가능성이 성립할 수 있습니다. 즉, 뉴런이 해석 가능한 특성을 가지려면, 먼저 특권적 기저가 존재해야 하며, 그 위에서 특성들이 정렬되는지를 살펴볼 수 있습니다.
요약:
- Privileged Basis: 신경망의 아키텍처적 요소(예: 활성화 함수)가 기저 방향을 특별하게 만들어서, 그 방향으로 특성들이 정렬되기 쉬운 경우. 이때 뉴런들이 해석 가능한 특성과 연결되기 쉽습니다.
- Non-privileged Basis: 특성들이 특정 기저와 정렬되지 않으며, 기저의 방향들이 특별한 의미를 가지지 않는 경우. 워드 임베딩처럼, 모든 방향이 동등하게 취급됩니다.
결론적으로, 특권적 기저가 존재하면 신경망에서 특성들이 기저 방향과 일치하여 해석 가능성이 높아지며, 이를 통해 특정 뉴런의 역할을 더 명확히 파악할 수 있습니다.
The Superposition Hypothesis
Privileged basis에 있는 경우에도 뉴런이 다의미적(Polysemantic)이고, 여러 관련 없는 특징에 반응하는 경우가 많다.
-> 중첩(Superposition) 가설
일반적으로 벡터를 저 차원에 투사하면 원래 벡터로 재 구성할 수 없다. 그러나 벡터가 희소하다면(feature가 희소하다) 벡터를 복구할 수 있다.


이 부분에서는 Superposition Hypothesis(중첩 가설)에 대해 설명하고 있습니다. 이 가설은 신경망이 차원 수보다 더 많은 특성(feature)을 어떻게 표현할 수 있는지에 대한 설명입니다. 이 개념은 신경망이 제한된 수의 뉴런을 가지고도 훨씬 더 많은 특성을 저장하고 처리할 수 있는 이유를 설명하려고 합니다.
1. Superposition Hypothesis(중첩 가설)란?
- Superposition Hypothesis는 신경망이 표현해야 하는 특성의 수가 뉴런의 수보다 많을 때 발생하는 현상을 설명합니다.
- 이 가설에 따르면, 신경망은 고차원 공간의 성질을 이용해 뉴런보다 더 많은 특성을 표현하려고 합니다. 결과적으로, 뉴런 하나가 여러 특성에 반응하는 경우가 발생하게 됩니다. 이때 뉴런은 polysemantic하게 동작하게 되며, 여러 가지 관련 없는 특성에 동시에 반응할 수 있습니다.
2. Superposition의 원리
- 신경망은 제한된 수의 뉴런을 사용하면서도 더 많은 특성을 표현하고 싶어하기 때문에, 고차원 공간에서의 수학적 성질을 활용하여 특성을 중첩해서 표현합니다. 이는 마치 작은 신경망이 큰 신경망을 시뮬레이션하는 것처럼 작동할 수 있습니다.
주요 수학적 개념:
- Almost Orthogonal Vectors(거의 직교하는 벡터):
- 수학적으로 n차원 공간에서는 최대 n개의 직교 벡터만 가질 수 있습니다. 직교 벡터란 서로 완전히 독립적인 벡터들로, 벡터 간의 코사인 유사도(cosine similarity)가 0인 벡터들입니다.
- 하지만, 고차원 공간에서는 거의 직교하는 벡터들이 많이 존재할 수 있습니다. 이러한 벡터들은 코사인 유사도가 0에 매우 가깝지만, 완벽하게 0은 아닌 "거의 직교" 상태입니다. 수학적으로, 이러한 벡터는 exp(n) 개 정도 존재할 수 있습니다. 즉, 차원이 커질수록 훨씬 더 많은 특성들이 거의 직교하는 벡터들로 표현될 수 있다는 뜻입니다.
- 이를 통해 신경망은 뉴런 수에 비해 훨씬 더 많은 특성을 표현할 수 있게 됩니다.
- Compressed Sensing(압축 감지):
- 일반적으로 벡터를 저차원 공간에 투영(projection)하면 원래 벡터를 복원할 수 없습니다. 정보가 손실되기 때문이죠.
- 하지만, 희소한 벡터(sparse vector)의 경우, 특성들이 드물게 활성화되는 특성을 이용하면 원래 벡터를 복원할 수 있습니다. 이는 압축 감지(compressed sensing)라는 기법에 해당합니다.
- 신경망에서도 특성들이 희소성(sparsity)을 띠면, 특성이 겹쳐 표현되는 상황에서도 원래 특성을 복원하거나 해석할 수 있게 됩니다.
3. Superposition의 동작 방식
- Superposition에서는 각 특성이 신경망의 뉴런 출력에서 거의 직교하는 방향으로 표현됩니다. 하지만 완전히 직교하지 않기 때문에, 하나의 특성이 활성화될 때 다른 특성들도 약간씩 활성화되는 현상이 발생합니다. 이러한 "간섭" 또는 "노이즈"가 발생하지만, 그 대가로 신경망은 훨씬 더 많은 특성을 표현할 수 있습니다.
- 예를 들어, 뉴런이 "고양이"라는 특성에 강하게 반응할 때, "자동차"나 "집" 같은 특성이 약하게 활성화될 수 있습니다. 이것이 거의 직교하는 특성들 간의 상호 간섭을 의미합니다.
- 이 간섭은 비용을 초래할 수 있지만, 특성이 희소(sparse)하다면, 이 비용을 감수할 수 있을 정도로 이득이 큽니다. 희소한 특성은 자주 활성화되지 않기 때문에, 특성 간의 간섭이나 노이즈를 효과적으로 걸러낼 수 있게 됩니다.
- 또한, 비선형 활성화 함수(activation function)가 작은 노이즈를 걸러내는 역할을 하기 때문에, 신경망은 특성 간의 간섭을 최소화하면서 많은 특성을 표현할 수 있습니다.
4. 작은 신경망이 큰 신경망을 시뮬레이션할 수 있음
- Superposition Hypothesis는 작은 신경망이 노이즈가 있는 큰 신경망을 시뮬레이션할 수 있음을 시사합니다. 즉, 작은 신경망은 차원이 부족하지만 여러 특성을 중첩하여 더 큰 신경망처럼 작동할 수 있습니다.
- 이는 고차원 공간에서 거의 직교하는 벡터의 성질을 이용해, 신경망이 더 많은 특성을 처리할 수 있게 해주는 메커니즘입니다.
5. 비특권적 기저(unprivileged basis)에서도 Superposition이 가능함
- Superposition은 특권적 기저(privileged basis)가 있는 신경망뿐만 아니라, 비특권적 기저(non-privileged basis)에서도 발생할 수 있습니다.
- 예를 들어, 워드 임베딩에서도 중첩 현상이 발생할 수 있습니다. 이때는 단순히 차원보다 더 많은 특성이 저장된다는 의미로 볼 수 있습니다. 즉, Superposition은 뉴런의 수나 공간의 차원보다 더 많은 특성을 표현할 수 있게 해주는 일반적인 원리입니다.
요약
- Superposition Hypothesis는 신경망이 뉴런의 수보다 더 많은 특성을 표현하기 위해 거의 직교하는 벡터와 희소성(sparsity)을 활용해 특성을 중첩해서 표현하는 메커니즘을 설명합니다.
- 이 가설에 따르면, 신경망은 고차원 공간의 성질을 이용해 특성들을 거의 직교하는 방향으로 표현하며, 특성 간의 간섭을 감수하고도 더 많은 특성을 처리할 수 있습니다.
- 희소성과 비선형 활성화 함수는 이러한 간섭을 최소화하여, 더 많은 특성을 효율적으로 표현할 수 있게 돕습니다.
이렇게 Superposition Hypothesis는 신경망이 제한된 뉴런 수로 더 많은 특성을 효율적으로 저장하고 처리하는 원리를 설명합니다.
그럼 여기서 희소성은 어떻게 나타나는거야? 특징이 별로 없는거야 뉴런이 별로 없는거야 가중치가 별로 없는거야?
여기서 말하는 희소성(sparsity)은 주로 뉴런의 활성화 상태와 관련이 있습니다. 즉, 많은 뉴런들이 대부분의 경우에 비활성화되고, 소수의 뉴런들만 특정 상황에서 활성화되는 상태를 의미합니다. 희소성은 다음과 같은 방식으로 나타날 수 있습니다:
1. 뉴런의 희소성:
- 희소성은 뉴런들이 특정 특성에만 반응하고, 대부분의 입력에 대해서는 비활성화되는 것을 말합니다. 즉, 뉴런들이 자주 활성화되지 않고, 일부 입력에 대해서만 활성화됩니다.
- 예를 들어, 어떤 뉴런이 "고양이"라는 특성에만 반응한다면, 그 뉴런은 "고양이" 이미지를 입력받았을 때만 활성화되고, 다른 상황에서는 비활성화될 것입니다. 이런 식으로, 많은 뉴런들이 특정한 상황에서만 활성화되기 때문에 활성화되는 뉴런의 수가 매우 적다는 의미에서 희소성이 나타납니다.
2. 특성의 희소성:
- 특성이 희소하다는 것은, 입력 데이터의 특정 **특성(feature)**이 전체 데이터에서 자주 나타나지 않는 것을 의미합니다. 즉, 소수의 특성들만 특정 입력에서 활성화되고, 나머지 특성들은 비활성화되는 경우입니다.
- 예를 들어, 이미지 데이터에서 "고양이의 눈"이라는 특성은 많은 이미지에서 나타나지 않을 수 있습니다. 이런 식으로 특정 특성이 데이터의 일부에만 활성화된다면, 이 특성은 희소한 특성이라고 할 수 있습니다.
3. 가중치의 희소성:
- 가중치의 희소성은 신경망에서 많은 가중치가 0에 가깝거나 매우 작은 값을 가진다는 것을 의미합니다. 즉, 많은 연결이 실제로는 거의 영향을 미치지 않는 상태를 의미합니다. 이러한 경우, 신경망은 주로 몇 개의 중요한 가중치만 사용하여 학습과 예측을 수행하게 됩니다.
- 하지만 중첩 가설에서 이야기하는 희소성은 가중치 자체의 희소성보다는 뉴런의 활성화 희소성이나 특성의 희소성에 더 가까운 개념입니다.
4. 희소성의 구체적 역할:
- 중첩 가설에서 희소성은 중요한 역할을 합니다. 희소성이 높을수록 여러 특성들이 서로 간섭하지 않고(즉, 특성이 겹쳐지지 않고) 고유하게 표현될 가능성이 커집니다. 다시 말해, 많은 뉴런들이 동시에 활성화되지 않고, 소수의 뉴런만이 활성화된다면 특성 간의 간섭이나 잡음을 줄일 수 있습니다.
- 특성들이 희소할 때, 한 뉴런이 동시에 여러 특성에 반응할 가능성(즉, polysemantic 뉴런이 될 가능성)이 높아질 수 있지만, 각 특성은 자주 활성화되지 않으므로 서로 간섭하는 일이 줄어듭니다. 따라서, 희소성 덕분에 중첩을 통해 많은 특성을 효율적으로 저장할 수 있습니다.
예시로 이해하기:
만약 신경망에서 100개의 뉴런이 있고, 그 중 10개만 활성화되며, 나머지 90개는 비활성화된다고 가정합시다. 이때 활성화된 10개의 뉴런만이 입력된 데이터의 특성들을 표현하게 됩니다. 특성들이 희소하게 활성화되기 때문에 각 뉴런이 겹치거나 간섭할 일이 적습니다. 즉, 한 번에 활성화되는 뉴런 수가 적고 대부분의 뉴런이 비활성화된 상태이므로, 특성들이 효과적으로 중첩되어 저장될 수 있습니다.
요약:
- 희소성은 신경망에서 소수의 뉴런이나 특성만이 활성화되고, 나머지는 대부분 비활성화된 상태를 의미합니다.
- 이는 뉴런의 수나 가중치가 적은 것을 뜻하기보다는, 특정한 상황에서만 뉴런들이 활성화되어 다른 뉴런들과 간섭하지 않게 만드는 구조를 의미합니다.
- 희소성 덕분에, 신경망은 잡음을 허용하면서 더 많은 특성을 중첩하여 표현할 수 있으며, 특성 간의 간섭을 최소화할 수 있습니다.
Demonstrating Superposition
linear model은 신경망이 가진 것 보다 더 많은 특징을 가지지 못하고, 주성분을 저장한다.
약간의 비선형성을 추가하면 다른 방식으로 동작한다!
고차원 신경망을 저차원 신경망이 표현할 수 있는지 알아보기 위해 실험을 진행한다.
m < n

큰 모델에서는 각각의 뉴런이 각각의 feature를 담당하게 된다
Feature Sparsity : 일반적으로 feature는 드물게 발생한다.
More Features Than Neurons : 모델이 표현할 수 있는 feature는 엄청 많다!
Features Vary in Importance : Feature마다 중요도가 다 다르다.
이 부분에서 "Feature는 sparse(희소)하다"고 말하면서도 동시에 "Neurons보다 Features가 많다"고 말하는 이유는, 특성(feature)의 희소성과 특성의 개수가 서로 다른 개념이기 때문입니다. 두 개념을 분리해서 이해하면 모순이 아닌 것을 알 수 있습니다.
1. Feature의 희소성(Sparsity)
특성(feature)이 희소하다(sparse)는 것은 특정 특성들이 드물게 활성화된다는 뜻입니다. 즉, 특성은 데이터의 대부분에서 나타나지 않고, 특정한 상황에서만 드물게 활성화됩니다. 예를 들어:
- 이미지 처리(vision)에서는 특정 이미지의 각 부분에 "수평선"이나 "곡선", "개 머리" 같은 특성이 나타나는 일이 드뭅니다. 이미지의 대부분에는 이런 특성이 없고, 특정한 위치에서만 나타나죠.
- 자연어 처리(language)에서도 "Martin Luther King"과 관련된 문맥은 많은 텍스트에서 등장하지 않습니다. 대부분의 단어들은 이와 관련이 없고, 특정한 문맥에서만 활성화됩니다.
이처럼 희소성은 특정 특성이 자주 나타나지 않거나 활성화되지 않는 상황을 의미합니다. 특정한 이미지나 문장 안에서는 해당 특성이 드물게 활성화될 뿐입니다.
2. Neurons보다 Features가 많다
Neurons보다 Features가 많다는 것은 모델이 표현할 수 있는 잠재적인 특성의 수가 신경망의 뉴런 수보다 더 많다는 뜻입니다. 이 두 가지 개념은 모순이 아닙니다. 그 이유는:
- 특성이 희소하다는 것은 각각의 특성이 자주 나타나지 않는다는 뜻이지, 전체 특성의 수가 적다는 것을 의미하지 않습니다.
- 사실상, 모델이 학습할 수 있는 잠재적인 특성의 수는 매우 많습니다. 예를 들어, 이미지를 처리하는 모델에서는 "수평선", "수직선", "곡선", "개 머리", "귀", "눈" 등 매우 많은 특성이 있을 수 있습니다. 이런 특성들이 모두 다를 수 있지만, 개별적으로는 매우 드물게 나타납니다.
따라서 특성의 수는 뉴런보다 많지만, 각 특성은 희소하게 나타나기 때문에 한 번에 활성화되는 특성은 상대적으로 적습니다.
3. 두 개념의 차이
- 희소성(sparsity)은 특정 데이터에서 많은 특성이 동시에 활성화되지 않고 소수만 활성화된다는 것을 말합니다. 예를 들어, 한 이미지나 문장에서는 많은 특성 중 극소수의 특성만 활성화될 수 있습니다.
- 반면, 특성의 수(features)는 모델이 잠재적으로 학습할 수 있는 모든 특성의 총합입니다. 이 특성의 총합은 매우 클 수 있지만, 각 데이터에서 동시에 나타나는 특성은 적습니다.
4. 왜 뉴런보다 특성이 많아야 할까?
현실 세계에서 다룰 수 있는 특성의 종류는 무한에 가깝습니다. 예를 들어:
- 이미지 처리 모델에서 "동물의 발톱", "하늘의 구름", "사람의 얼굴" 등 수많은 특성들이 중요할 수 있습니다.
- 언어 모델에서는 "감정", "주제", "문법적 구조" 같은 다양한 특성들이 필요할 수 있습니다.
그러나 모든 특성에 대해 뉴런 하나를 할당할 수는 없습니다. 뉴런의 수는 물리적, 계산적 한계 때문에 제한적이지만, 모델은 더 많은 특성을 처리해야 하므로, 하나의 뉴런이 여러 특성에 동시에 반응할 수 있어야 합니다. 이것이 중첩(superposition)의 개념으로 연결됩니다. 즉, 하나의 뉴런이 여러 특성을 중첩해서 표현하는 방식으로 더 많은 특성을 처리할 수 있습니다.
5. 결론
- 희소성은 특정한 입력에서 활성화되는 특성의 수가 적다는 의미입니다. 한 번에 많은 특성이 활성화되지 않지만, 전체적으로 보면 특성의 수는 여전히 매우 많을 수 있습니다.
- 특성의 개수는 뉴런의 수보다 많다는 것은 모델이 처리할 수 있는 잠재적인 특성의 수가 매우 크며, 신경망의 뉴런 수로 모든 특성을 독립적으로 처리할 수 없음을 뜻합니다.
- 신경망은 중첩(superposition)을 사용하여 적은 뉴런 수로 더 많은 특성을 표현하고 처리하려고 합니다.
결론적으로, 특성의 희소성과 특성의 개수가 많다는 것은 상호 배타적이지 않습니다. 데이터에서 특정 특성들이 자주 활성화되지 않더라도, 모델이 처리해야 하는 특성의 총 수는 매우 클 수 있기 때문입니다.
Experiment

W를 transpose하여 벡터 복구에 사용한다.
bias를 추가하여 노이즈를 버리고, 표현하지 않은 feature를 예상 값으로 설정 할 수 있다.
마지막 layer에 activation을 추가한 이유는 실제 신경망에서도 activation을 포함하는 것이 일반적이기 때문이다.

Experiment Result

Wi를 통해 feature의 표현 여부가 결정된다.

이 식을 통해 feature의 활성화 정도 및 중첩 정도를 알 수 있게 된다.

이 그림과 텍스트는 중첩 현상(superposition)을 통해 모델이 어떻게 특성들을 표현하는지, 그리고 특성 간의 직교성(orthogonality)을 시각적으로 분석하는 방법을 설명하고 있습니다. 여기서 중첩이란, 특성들이 서로 독립적이지 않고 겹치는 방식으로 저장되며, 신경망이 제한된 뉴런으로 더 많은 특성을 처리하기 위한 방법을 말합니다.
1. 특성 벡터의 노름(Norm of Feature Vector, ||W_i||):
- ||W_i||는 특성 i에 대한 가중치 벡터 W_i의 크기(norm)를 나타냅니다. 이는 해당 특성이 얼마나 잘 표현되었는지를 나타내는 척도입니다.
- ||W_i|| 값이 1에 가까우면 그 특성은 완전히 표현되었고, 값이 0에 가까우면 그 특성은 거의 표현되지 않았다는 뜻입니다.
- 이 그림에서는 가로 막대를 통해 각 특성의 ||W_i|| 값을 나타내며, 특성이 얼마나 중요하고 잘 표현되었는지 쉽게 시각화할 수 있습니다. 검은색 선이 ||W_i||의 크기이며, 1에 가까울수록 특성이 잘 표현되었음을 의미합니다.
2. 특성 간의 직교성 여부 (Orthogonality and Superposition):
- 직교성(orthogonality)은 두 벡터가 서로 완전히 독립적임을 의미합니다. 즉, 두 벡터가 직교하면 한 벡터가 활성화될 때 다른 벡터에 영향을 미치지 않습니다.
- 중첩(superposition)이란 두 특성이 비직교(non-orthogonal)하여 하나의 특성이 활성화될 때, 다른 특성들도 약간씩 활성화되는 현상을 의미합니다. 즉, 특성들이 서로 겹쳐서 표현되는 것입니다.
- 이를 수학적으로 분석하기 위해 다른 모든 특성들을 특정 특성의 방향으로 투영(projection)하여 그 합을 계산합니다:
- 이 값이 0에 가까우면 해당 특성은 다른 특성과 직교(독립적)하다는 의미입니다. 즉, 특성이 다른 특성들과 거의 영향을 주고받지 않으며 독립적으로 표현된다는 뜻입니다.
- 값이 1 이상이면, 그 특성은 다른 특성과 강하게 겹쳐져서 표현되고 있다는 뜻입니다. 즉, 특성 i는 다른 특성들과 차원을 공유하면서, 동시에 활성화될 수 있습니다.
3. 색상에 따른 시각화 (Superposition 색상 막대):
- 색상을 통해 각 특성이 다른 특성과 얼마나 직교하는지(혹은 겹치는지)를 시각적으로 보여줍니다.
- 어두운 파란색은 특성이 다른 특성과 직교적(완전히 독립적)이라는 것을 의미합니다. 즉, 이 특성은 중첩 없이 독립적으로 표현되고 있습니다.
- 밝은 노란색은 해당 특성이 다른 특성과 강하게 겹치고(중첩) 있음을 의미합니다. 즉, 이 특성은 여러 다른 특성과 동일한 차원을 공유하며 동시에 활성화될 수 있습니다.
4. 이 모델의 결과 해석:
- 이 모델은 가장 중요한 특성들에 대해 각 특성마다 하나의 차원을 할당하고 있습니다. 즉, 이 특성들은 직교적으로 표현되고 있으며, 서로 간섭하지 않고 독립적으로 표현됩니다.
- 특성 간의 중첩이 발생하지 않음을 보여주고 있습니다. 이는 모델이 중첩을 허용하지 않고, 각 특성을 개별적으로 잘 표현하려는 경향을 시사합니다.
요약:
- 이 실험의 시각화는 특성이 얼마나 독립적으로 표현되는지, 혹은 특성이 서로 중첩되어 표현되는지를 분석합니다. ||W_i|| 값으로 특성의 표현 정도를, 색상으로 특성 간의 중첩 정도를 나타냅니다.
- 이 모델은 주로 중첩 없이 직교적으로 특성들을 표현하고 있으며, 각 특성에 하나의 차원을 할당하여 가장 중요한 특성들을 독립적으로 표현하고 있습니다.
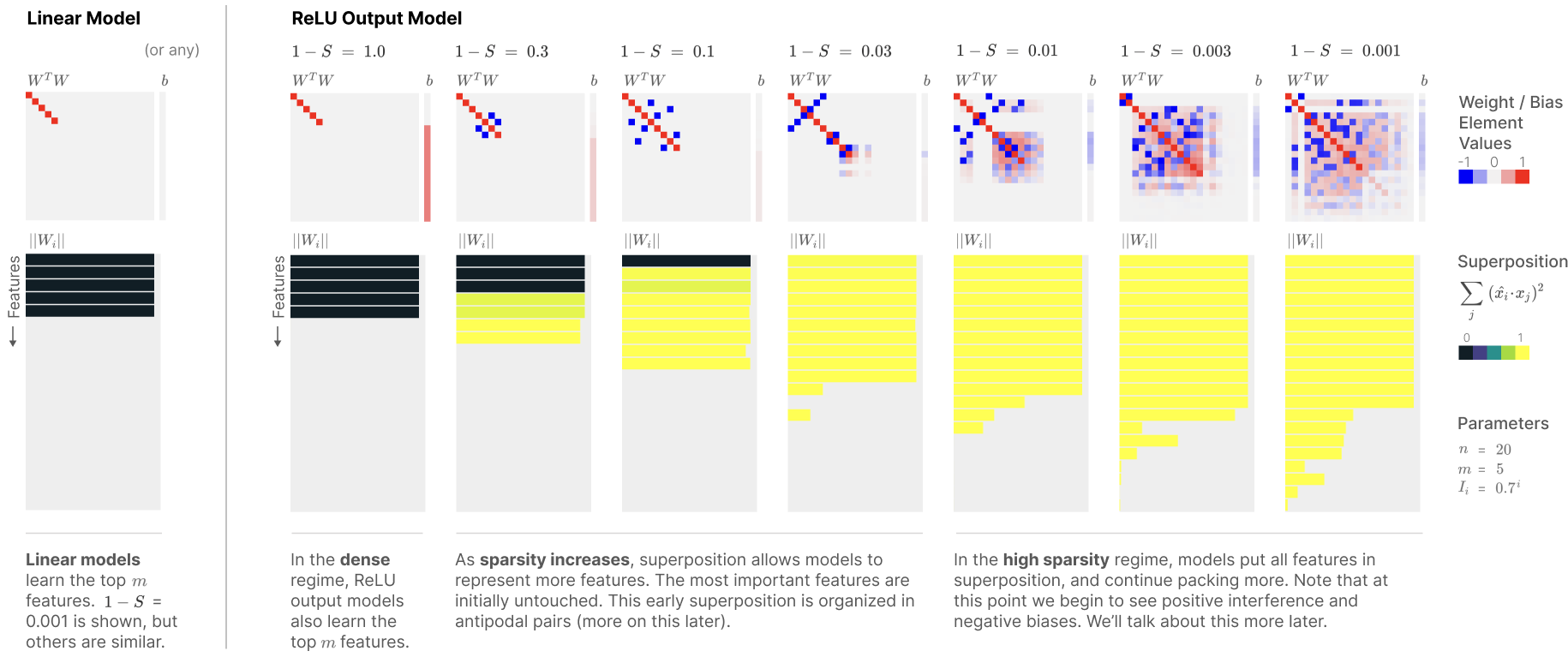
그럼 이 사진에서의 변화는 선형 모델일 때는 m=5개이므로 5개의 특징만 뽑아서 결과로 진행하였는데 비선형성이 추가되고, sparse한 feature가 늘어날 수록 중첩이 생겨서 W^T*W연산에서 안쓰는 feature를 버리기 위해 파란색이 늘어나고, 중첩을 표현하는 노란색이 늘어나는거야?
네, 정확하게 이해하셨습니다! 이제 각 부분을 조금 더 자세히 설명해 드릴게요.
1. 선형 모델 (왼쪽 부분):
- 선형 모델의 경우, 모델은 m = 5개의 가장 중요한 특성만 학습합니다. 이는 선형 모델이 항상 상위 m개의 주요 특성에 집중한다는 점을 보여줍니다.
- W^T * W 행렬에서는 대각선 요소만 존재하는데, 이는 각 특성이 서로 직교(독립적)임을 나타냅니다. 직교는 하나의 특성이 활성화될 때 다른 특성에 영향을 미치지 않는다는 의미입니다.
- 따라서, 이 모델에서는 중첩이 발생하지 않으며, 모든 특성은 독립적으로 표현됩니다. 이 경우 ||W_i|| 값도 상위 5개의 특성에만 활성화된 상태를 보여줍니다.
2. ReLU 모델에서 희소성(Sparsity)에 따른 변화 (오른쪽 부분):
- ReLU 출력 모델에서는 희소성(Sparsity)의 정도에 따라 중첩(superposition) 현상이 발생합니다.
- 1 - S = 1.0일 때, 즉 dense(밀집)한 특성일 경우, ReLU 모델은 선형 모델처럼 상위 5개의 특성만을 학습하고, 서로 직교한 방식으로 표현합니다.
3. 희소성이 증가하면서 중첩이 발생하는 과정:
- Sparsity(희소성)가 증가하면서, 즉 1 - S가 줄어들수록, 중첩이 나타납니다. 이를 그림에서 볼 수 있는 주요 변화로 설명할 수 있습니다:
- W^T * W 행렬에서 파란색 요소들이 나타나기 시작합니다. 이는 특성들이 서로 겹치기 시작했음을 의미합니다. 파란색 요소는 특성 간의 상호작용(비직교성)을 나타냅니다. 즉, 한 특성이 활성화되면 다른 특성도 조금씩 활성화되며, 간섭이 발생하는 것이죠.
- ||W_i|| 값을 시각화한 하단의 노란색 막대는 중첩의 정도를 나타냅니다. 노란색이 많을수록, 더 많은 특성이 비직교적으로 겹쳐져서 표현되고 있다는 의미입니다.
- 희소성이 높아질수록, 더 많은 특성이 중첩되어 더 적은 뉴런으로 더 많은 특성을 표현하려고 합니다. 1 - S 값이 작아질수록 중첩 현상이 더 뚜렷해지며, 노란색 막대가 점점 더 커집니다.
4. 중첩(superposition)의 효과:
- 희소성(Sparsity)가 커지면서 모델은 더 많은 특성을 표현하기 위해 중첩(superposition)을 사용합니다.
- 파란색 요소가 더 많아지는 것은 특성 간의 비직교성이 증가하고 있음을 나타냅니다.
- 노란색 막대가 더 커지고 있다는 것은 특성들이 비직교적으로 겹쳐져서, 하나의 뉴런이 여러 특성을 동시에 표현하고 있음을 시사합니다.
- 희소성이 매우 커질 때, 즉 1 - S = 0.001과 같은 경우, 거의 모든 특성이 중첩된 방식으로 표현됩니다. 이때 W^T * W 행렬에서 다양한 색깔의 패턴을 볼 수 있는데, 이는 모델이 각 특성 간의 상호작용을 처리하기 위해 더욱 복잡한 구조로 학습되고 있음을 보여줍니다.
5. 결론:
- 선형 모델은 상위 m = 5개의 특성만 독립적으로 표현하며, 중첩이 발생하지 않습니다.
- ReLU 모델은 희소성(Sparsity)이 증가할수록, 즉 특성들이 더 드물게 활성화될수록, 중첩 현상이 발생합니다. 특성들이 비직교적인 방식으로 겹쳐져서 하나의 뉴런이 더 많은 특성을 처리하게 되고, 이는 파란색과 노란색으로 시각화됩니다.
따라서, 중첩을 통해 모델은 더 적은 뉴런으로 더 많은 특성을 처리할 수 있게 되지만, 그 대가로 특성 간의 간섭을 감수해야 합니다.
희소성은 어떻게 늘리나? -> 특성들이 입력 데이터에서 드물게 나타나도록 하여 적은 수의 특성만 활성화 되도록
희소성이 증가하면서 중첩이 나타나 더 많은 feature를 표현하게 된다.
덜 중요한 feature부터 시작하여 점차 중요한 feature까지 영향을 미친다.
여기서 노란색이 덜 채워진 부분은 기하학적 다양성을 뜻한다!

이 부분은 실험 결과를 설명하는 섹션으로, 중첩(superposition)이 신경망에서 어떻게 발생하는지를 시각적으로 확인하려는 시도를 설명합니다. 실험에서는 희소성(sparsity)이 달라짐에 따라 ReLU 출력 모델과 선형 모델의 동작을 비교하고, 중첩이 어떻게 나타나는지를 살펴봅니다. 주요 실험 결과를 정리하면 다음과 같습니다.
1. 실험 설계
- ReLU 출력 모델과 선형 모델을 여러 희소성 수준에서 학습합니다. 선형 모델의 경우 희소성에 상관없이 고유 차원 수(n)에 해당하는 특성만을 학습하게 됩니다. 반면, ReLU 모델은 희소성 수준에 따라 다르게 동작하며, 중첩 현상이 발생합니다.
- 희소성 수준이란, 데이터에서 특정 특성들이 얼마나 자주 활성화되느냐를 의미합니다. 희소성 수준이 높을수록 특정 특성들이 덜 자주 나타나며, 이를 통해 모델이 중첩을 어떻게 처리하는지 확인할 수 있습니다.
2. W^T W와 b의 시각화
- 실험에서 결과를 시각화하는 첫 번째 방법은 W^T W 행렬과 b 벡터입니다.
- W^T W: 이는 특성 간의 관계를 보여주는 특성 간의 내적(matrix of feature by feature)입니다. 즉, 각 특성이 서로 얼마나 연관되어 있는지를 보여주는 행렬입니다.
- b: 특성의 길이를 나타내는 벡터입니다. 특성의 길이(norm)는 특성이 얼마나 중요한지를 나타냅니다. 중요한 특성일수록 길이가 더 큽니다.
- 결과를 해석할 때, 특성들은 중요도에 따라 배열되며, 이로 인해 시각화된 결과가 구조적으로 잘 보입니다. 모델의 학습된 결과는 가장 중요한 특성부터 덜 중요한 특성까지 배열됩니다.
3. 중첩 현상을 명시적으로 탐구
- 중첩(superposition)이 발생하는지 확인하는 중요한 방법은 모델이 얼마나 많은 특성을 학습하는지를 보는 것입니다. 특성이 학습되었는지는 해당 특성의 가중치 벡터(W_i)의 크기(norm)로 판단할 수 있습니다.
- 또한, 특성이 서로의 차원을 공유하는지를 알아보기 위해, 각 특성의 가중치 벡터(W_i)가 다른 특성들의 가중치 벡터와 얼마나 관련 있는지를 계산합니다. 이를 위해 다음과 같은 계산을 합니다:
∑j≠i(Wi⋅Wj)^2이 값은, 특성 i의 가중치 벡터가 다른 특성 j와 얼마나 많이 겹치는지를 보여줍니다.- 0에 가까울수록, 해당 특성은 다른 특성과 직교(독립적)하다는 것을 의미합니다.
- 값이 1 이상이면, 여러 특성들이 동시에 활성화되어 특정한 차원을 공유할 수 있습니다. 즉, 한 뉴런이 여러 특성에 반응할 수 있음을 뜻하며, 이는 polysemantic 뉴런의 개념과 연결됩니다.
4. ReLU 모델에서 중첩의 결과
- 선형 모델은 항상 상위 m개의 가장 중요한 특성만을 학습하며, 이는 주성분 분석(Principal Component Analysis)과 유사한 방식으로 차원 수와 일치하는 특성만을 선택합니다.
- 그러나 ReLU 출력 모델에서는, 특성의 희소성(sparsity)이 증가함에 따라 중첩(superposition)이 나타납니다. 즉, 특성들이 더 이상 서로 직교하지 않고, 겹치면서 더 많은 특성을 표현하려고 합니다.
- 희소성 증가에 따른 중첩의 변화:
- 처음에는 덜 중요한 특성들부터 중첩되기 시작합니다.
- 이후 더 중요한 특성들까지 차차 중첩에 영향을 받습니다.
- 처음 중첩이 발생할 때, 대칭적인 형태로 특성들이 반대 방향(antipodal pairs)으로 배열됩니다. 예를 들어, 한 특성의 벡터가 +1 방향이면, 다른 특성은 -1 방향으로 표현됩니다. 이후에는 이 배열이 더 복잡한 기하학적 구조로 발전하면서, 점점 더 많은 특성을 표현할 수 있게 됩니다.
5. 더 큰 모델에서도 유사한 결과
- 모델의 차원 수(m)가 더 큰 모델에서도 유사한 결과가 나타납니다.
- 예를 들어, m=20(숨겨진 차원 수)과 n=80(특성 수)을 가지는 더 큰 모델에서는, 차원이 커진 만큼 시각적으로 확장된 형태로 비슷한 결과를 확인할 수 있습니다.
- 즉, 차원이 증가하더라도 중첩 현상은 여전히 발생하며, 모델은 뉴런 수보다 많은 특성을 처리하기 위해 비직교적인 방식으로 특성들을 배치합니다.
요약:
- 선형 모델은 항상 상위 m개의 가장 중요한 특성만을 학습하며, 각 특성은 서로 직교합니다.
- ReLU 모델은 희소성이 증가함에 따라 중첩을 통해 더 많은 특성을 처리하려고 하며, 각 특성들이 비직교적인 방식으로 표현됩니다.
- 중첩은 처음에는 대칭적 형태로 발생하지만, 점점 더 복잡한 기하학적 구조로 변형되면서 더 많은 특성을 표현하게 됩니다.
Mathematical Understanding
중첩이 나타나는 수학적 이유는? - feature benefit, interference
linear 에서는 왜 중첩이 발생하지 않는가?

모델은 더 많은 feature를 표현할 수 있으면 더 낮은 loss를 얻을 수 있지만 직교 범위를 넘어가면 간섭이 생겨서 오히려 loss를 늘린다. - 이로 인해 선형 모델이 차원 보다 많은 특성을 표현하는 것은 의미가 없다.

bias를 통해 음의 간섭과, 작은 양의 간섭을 지운다
이 부분은 선형 모델과 ReLU 모델에서 특성 표현 방식의 차이를 수학적으로 설명하는 내용입니다. 특히 중첩(superposition)이 선형 모델에서 발생하지 않고, ReLU 활성화 함수가 있는 모델에서 발생하는 이유를 설명합니다. 이와 관련된 수식을 분석하면서, 특성 표현에 따른 이익(Feature benefit)과 특성 간 간섭(Interference)이라는 두 가지 주요 힘이 신경망의 학습을 어떻게 조절하는지에 대해 설명합니다.
1. 선형 모델의 손실 함수 (첫 번째 수식)
수식:

설명:
- 첫 번째 항은 특성 이익(Feature benefit)을 나타냅니다. 특성 i가 신경망에 의해 정확하게 표현되었을 때 모델이 얻는 이익을 의미합니다.
- ∥Wi∥는 특성 벡터의 크기(norm)를 나타냅니다.
- 이 항에서 1 - || W_i ||^2는 특성 i가 완전히 표현되었을 때 (즉, ∥Wi∥=1) 손실이 0이 됨을 의미합니다. 이때 특성이 완벽하게 표현되었기 때문에 더 이상 손실을 줄일 필요가 없습니다.
- 반대로, ∥Wi∥=0일 때는 그 특성이 전혀 표현되지 않았으므로 손실이 큽니다.
- 두 번째 항은 특성 간 간섭(Interference)을 나타냅니다. 두 특성 i와 j가 비직교적(non-orthogonal)일 때 발생하는 간섭을 의미합니다.
- Wj⋅Wi는 두 특성 벡터 간의 내적을 나타내며, 이는 두 특성이 얼마나 비직교적인지를 측정합니다.
- 이 값이 클수록 두 특성은 서로 영향을 많이 미치며, 이는 손실을 증가시킵니다. 선형 모델에서는 특성 간 간섭을 줄이기 위해 특성들이 직교하려고 하며, 이로 인해 중첩이 발생하지 않습니다.
요약:
- 선형 모델에서는 특성 간 간섭을 피하려고 특성들이 직교하게 학습됩니다. 따라서, 선형 모델에서는 중첩(superposition)이 발생하지 않고, 모델은 특성의 개수만큼만 정확하게 표현합니다.
2. ReLU 모델의 손실 함수 (두 번째 수식)
수식:

설명:
- 첫 번째 항은 특성 이익을 나타냅니다. 선형 모델과 유사하지만, ReLU 활성화 함수가 추가되었습니다.
- ReLU는 0보다 작은 값은 모두 0으로 만들기 때문에, 비선형성을 도입합니다. 이로 인해 특성 간 간섭이 발생할 때도 ReLU는 일부 간섭을 완전히 제거하거나 줄일 수 있습니다.
- 즉, ReLU는 손실을 더 나쁘게 만들지 않으며, 편향(bias) bi가 모델이 정확히 표현하지 못하는 특성에 대해 평균적인 값을 취하도록 도와줄 수 있습니다.
- 두 번째 항은 특성 간 간섭(Interference)을 설명합니다. 선형 모델과 달리, ReLU는 특성 간의 음성 간섭(negative interference)을 완전히 제거할 수 있습니다.
- 예를 들어, ReLU 활성화 함수는 음의 간섭을 0으로 만들어 간섭이 없는 상태로 만듭니다. 이는 특히 1-희소성(1-sparse)인 상황에서 중요합니다. 이때, 간섭이 없는 상태에서 더 많은 특성이 중첩될 수 있게 만듭니다.
- 즉, ReLU 활성화 함수는 특성 간 양의 간섭을 줄이고, 음의 간섭을 제거하여 중첩 현상을 허용하는 역할을 합니다.
요약:
- ReLU 모델에서는 비선형성이 추가됨으로써, 특성 간의 음의 간섭을 제거하거나 줄일 수 있습니다. 이로 인해 특성들이 서로 간섭을 덜 하게 되고, 같은 차원에서 여러 특성을 중첩할 수 있습니다.
3. ReLU 모델에서 1-희소성(1-Sparsity)의 역할
- 희소성이란 특정 특성들이 드물게 활성화되는 상태를 말합니다. ReLU 모델에서, 희소성이 증가하면 ReLU는 더 많은 간섭을 줄일 수 있으며, 이로 인해 중첩(superposition)이 더 많이 발생합니다.
- ReLU는 음의 간섭을 제거하여 모델이 더 많은 특성을 표현할 수 있게 도와줍니다. 이로 인해 중첩이 발생할 수 있으며, 이는 선형 모델에서 나타나지 않는 현상입니다.
4. Thomson 문제와의 유사성
ReLU 모델에서, 중첩이 발생하는 방식은 화학에서의 Thomson 문제와 비슷한 구조를 가지고 있습니다. Thomson 문제는 전자들이 서로의 반발력을 최소화하면서 구의 표면에 어떻게 배열되는지에 관한 문제입니다. ReLU 모델에서, 특성들이 최소한의 간섭을 가지면서도 최대한 많은 특성을 표현하려는 방식이 Thomson 문제의 배열 방식과 유사합니다.
결론:
- 선형 모델에서는 특성 간 간섭을 피하려고 특성들이 직교하게 학습되므로, 중첩이 발생하지 않습니다.
- ReLU 모델에서는 비선형성을 추가함으로써, 특성 간 간섭을 줄이거나 제거하여 중첩을 허용할 수 있습니다. 이로 인해, ReLU 모델은 선형 모델과 달리 더 많은 특성을 하나의 뉴런에서 표현할 수 있습니다.
- 이러한 방식은 희소성(sparsity)에 따라 더 두드러지게 나타나며, Thomson 문제와 같은 방식으로 특성들이 최소한의 간섭을 가지면서 배열됩니다.
Superposition as a Phase Change
위의 결과를 보고 우리는 3개로 추릴 수 있다.
1. feature는 단순히 학습되지 않는다.
2. feature는 학습되어 중첩으로 표현될 수 있다.
3. model은 feature를 특정한 차원에서 표현한다.
중요도와 sparse를 조절하여 실험해본다.

중첩이 발생하려면 희소성도 필요하지만 중요도도 필요하다!
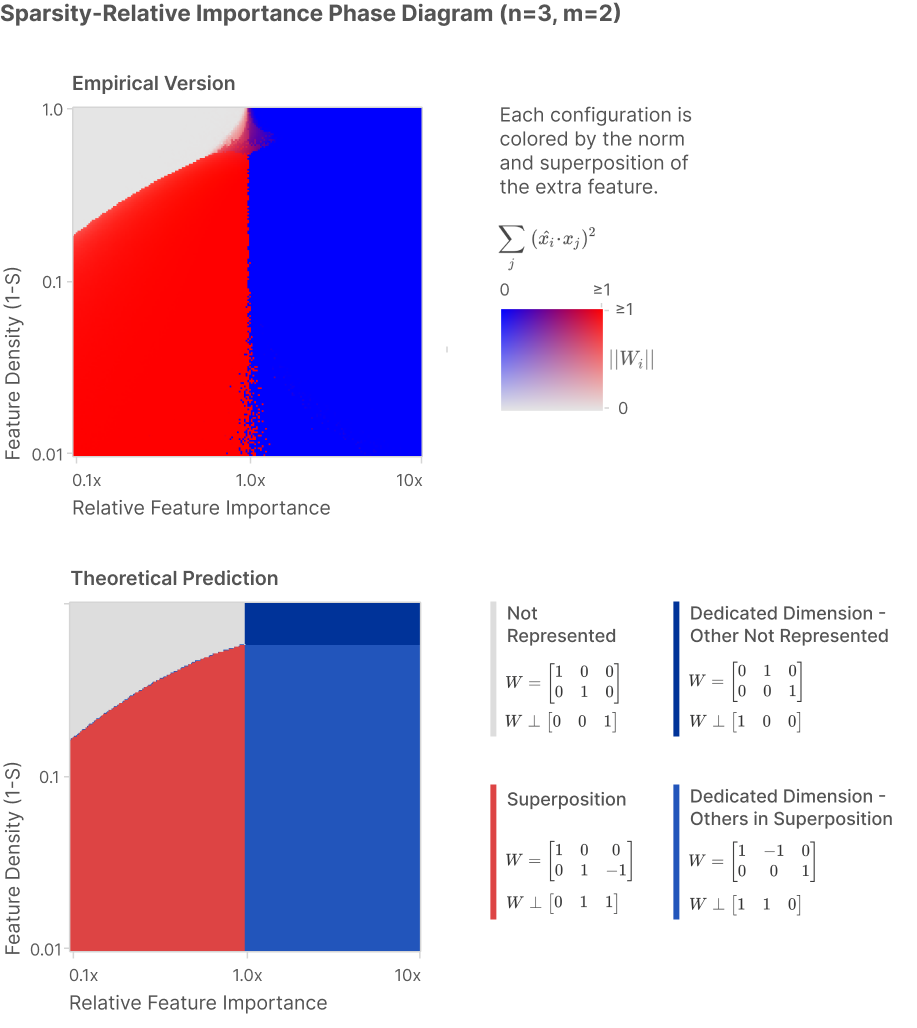
이 이미지와 설명은 특성(feature)들이 모델에서 어떻게 표현되는지에 대한 다양한 경우를 Phase Diagram(상 변화도) 형식으로 나타낸 것입니다. 특히 희소성(Sparsity)과 특성의 상대적 중요도(Relative Feature Importance)가 달라질 때, 모델이 특정 특성을 어떻게 표현하는지에 대한 세 가지 가능성을 보여줍니다:
- 특성이 전혀 학습되지 않음 (Not Represented).
- 특성이 중첩(superposition)된 방식으로 표현됨.
- 특성이 전용 차원(dedicated dimension)에서 표현됨.
1. Phase Diagram 설명:
- X축: Relative Feature Importance(상대적 중요도)를 나타냅니다. 이는 한 특성이 다른 특성에 비해 얼마나 중요한지를 나타냅니다.
- Y축: Feature Density(1 - S)로, 이는 희소성(Sparsity)을 나타냅니다. 값이 1에 가까울수록 특성이 자주 활성화되고, 값이 작을수록 특성이 희소하게 나타나는 상황을 의미합니다.
이 두 축을 바탕으로 특성들이 어떻게 표현되는지 세 가지 경우로 나뉩니다:
2. 세 가지 결과:
- Not Represented(특성이 표현되지 않음 - 회색):
- 특성의 상대적 중요도가 매우 낮고 희소성이 낮을 때, 모델은 해당 특성을 학습하거나 표현하지 않습니다.
- 이 경우, 해당 특성은 모델이 완전히 무시하게 됩니다.
- Superposition(중첩 - 빨간색):
- 중첩(superposition)은 하나의 뉴런이 여러 특성을 동시에 표현하는 상황입니다. 즉, 두 특성이 같은 차원에서 함께 표현되며, 이로 인해 간섭(interference)이 발생할 수 있습니다.
- 희소성이 높을 때 중첩이 잘 발생하며, 상대적으로 중요도가 낮은 특성들이 함께 표현됩니다.
- 빨간색 영역에서는 모델이 특성들을 중첩된 방식으로 표현하는 것을 보여줍니다. 이 경우 하나의 차원에서 여러 특성이 함께 저장됩니다.
- Dedicated Dimension(전용 차원에서 표현 - 파란색):
- 특성의 상대적 중요도가 높거나, 다른 특성에 비해 매우 중요할 때, 모델은 그 특성을 전용 차원(dedicated dimension)으로 표현하게 됩니다.
- 파란색 영역에서는 특정 특성이 다른 특성과 분리되어 독립적으로 표현됩니다. 즉, 그 특성은 간섭 없이 독립된 차원에서 처리됩니다.
3. Phase Change (상 변화):
- 여기서 핵심 개념은 Phase Change(상 변화)입니다. 특성의 상대적 중요도와 희소성에 따라 특성이 표현되는 방식이 갑자기 변하는 것을 의미합니다.
- 예를 들어, 희소성이 낮고 상대적 중요도가 낮은 특성은 무시되지만, 희소성이 높아지면 그 특성은 중첩된 방식으로 표현되기 시작합니다. 또한, 상대적 중요도가 충분히 높아지면 중첩에서 벗어나 전용 차원에서 독립적으로 표현됩니다.
- 이러한 상 변화는 특성 표현 방식이 특정 지점에서 급격히 변함을 의미하며, 이는 물리학에서의 상 변이(Phase Transition)와 유사한 개념입니다.
4. 이론적 모델과 실험적 모델 비교:
- Empirical Version(실험적 결과): 실제 신경망 학습에서 관측된 데이터를 기반으로 한 실험적 결과입니다. 여기서는 중첩된 영역(빨간색)과 전용 차원(파란색)으로 특성이 나뉩니다.
- Theoretical Prediction(이론적 예측): 이론적으로 계산된 결과입니다. 이론적으로도 실험적 결과와 비슷한 패턴을 보여주며, 특정 희소성과 중요도에서 중첩에서 전용 차원으로 상 변환이 발생하는 것을 확인할 수 있습니다.
요약:
이 두 다이어그램은 특성의 상대적 중요도와 희소성에 따라 특성이 모델에서 무시되거나, 중첩되어 표현되거나, 독립된 차원에서 표현되는 세 가지 경우를 보여줍니다. 중요한 것은 희소성과 중요도가 일정 수준을 넘을 때 모델이 특성을 표현하는 방식이 급격히 변한다는 점입니다. 이러한 변화를 상 변화(Phase Change)라고 부르며, 이는 특성 학습과 표현 방식에 중요한 개념입니다.
The Geometry of Superposition
Superposition - 여러 feature를 표현 가능
increase sparsity - 추가적인 feature 표현 가능
Uniform Superposition
모든 feature들이 동일한 중요도와 sparsity를 가지는 uniform한 superposition으로 시작
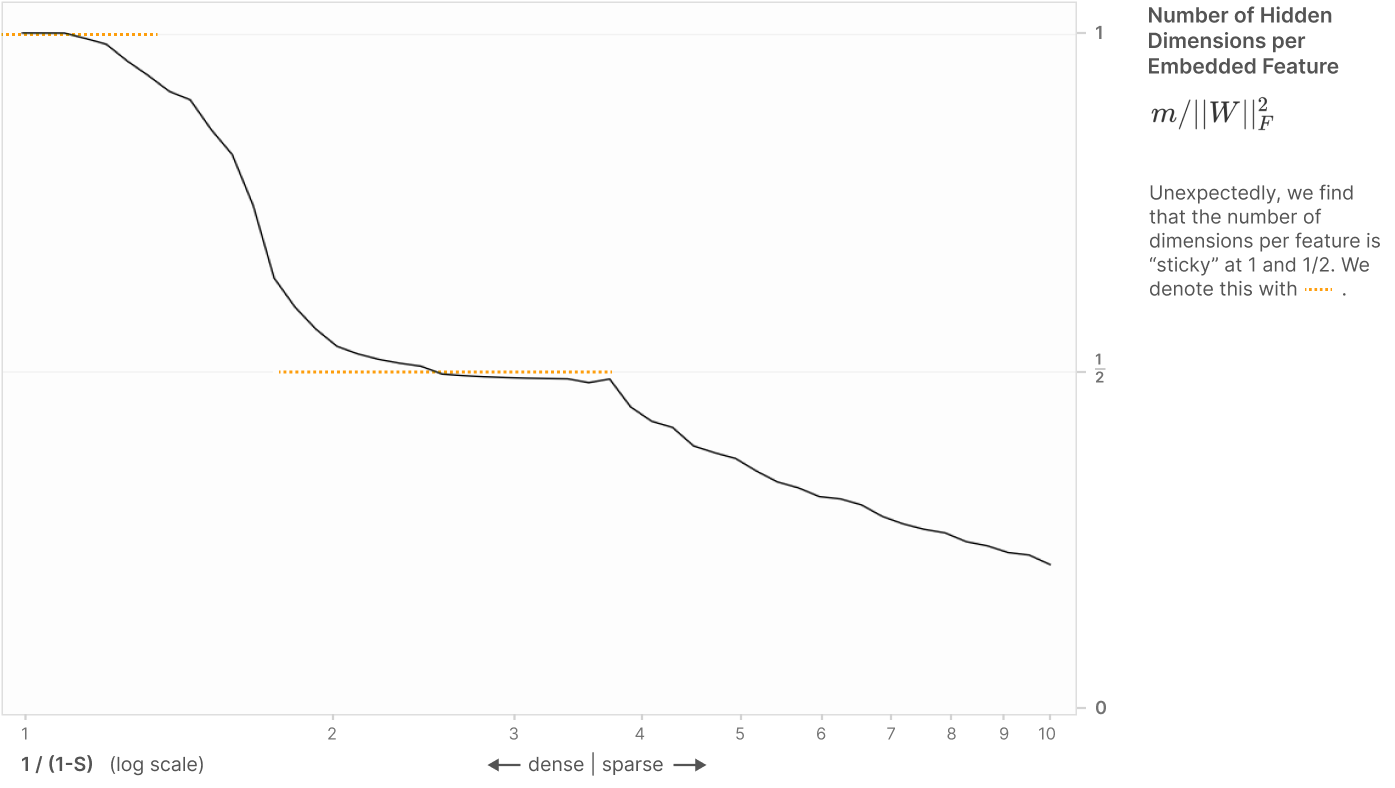
이 그래프는 중첩(superposition)의 기하학적 구조를 조사하는 과정에서 나타난 흥미로운 결과를 보여줍니다. 특히, 특성들이 모델의 숨겨진 차원(hidden dimensions)에 어떻게 배치되는지와 희소성(sparsity)에 따라 어떻게 변하는지를 시각화합니다.
그래프의 축과 주요 요소:
- X축: 1/(1-S)로 표현되며, 희소성의 역수를 나타냅니다.
- 왼쪽으로 갈수록 데이터가 밀집(dense)된 상태이고, 오른쪽으로 갈수록 데이터가 희소(sparse)한 상태입니다.
- Y축: 임베딩된 특성 당 숨겨진 차원 수 (m / ||W||2F)를 나타냅니다.
- 여기서 m은 모델의 숨겨진 차원 수를 나타내고, ||W||2F는 가중치 행렬 W의 프로베니우스 노름(Frobenius norm)입니다. 이 값은 모델이 학습한 특성의 수를 나타내는 척도로 사용됩니다.
그래프의 의미:
- 밀집한 영역(좌측):
- 1/(1-S) 값이 작을 때 (즉, S가 1에 가까울 때), 데이터는 밀집(dense)한 상태에 있습니다.
- 이 영역에서 숨겨진 차원 수는 주로 1 근처에 "붙어(sticky)" 있습니다.
- 이 의미는, 하나의 숨겨진 차원이 한 개의 특성을 표현하는 데 사용된다는 것입니다.
- 희소한 영역(우측):
- 1/(1-S) 값이 클 때 (즉, S가 0에 가까울 때), 데이터는 희소(sparse)한 상태에 있습니다.
- 이 영역에서는 숨겨진 차원 수가 점차적으로 줄어들며, 특히 1/2 지점에서 "붙어(sticky)" 있습니다.
- 이 의미는, 하나의 숨겨진 차원이 두 개의 특성을 표현하는 데 사용된다는 것입니다. 즉, 두 개의 특성이 안티포달 쌍(antipodal pairs) 형태로 중첩되어 하나의 차원에 배치됩니다.
"Sticky" 현상:
- 그래프에서 발견되는 놀라운 점은, 숨겨진 차원 수가 1과 1/2에서 "붙어 있는(sticky)" 현상입니다.
- 1에서의 "붙음"은, 일반적인 상황에서 하나의 숨겨진 차원이 하나의 특성을 표현한다는 것을 나타냅니다.
- 1/2에서의 "붙음"은, 안티포달 쌍(antipodal pairs)이 나타나는 상태로, 두 개의 특성이 서로 반대되는 방향으로 배열되어 하나의 숨겨진 차원에 함께 표현된다는 것을 나타냅니다.
왜 이런 현상이 나타나는가?
- 안티포달 쌍(antipodal pairs):
- 이 쌍은 두 특성이 서로 정확히 반대되는 방향으로 표현되며, 이로 인해 하나의 숨겨진 차원에 두 특성을 효율적으로 표현할 수 있습니다.
- 이것은 모델이 더 많은 특성을 표현하기 위해 공간을 최적화하는 방식 중 하나로 작동합니다.
- 희소성 증가에 따른 효과:
- 희소성이 증가할수록, 즉 데이터가 더 희소해질수록, 모델은 더 많은 특성을 표현하려고 노력합니다.
- 이 과정에서 모델은 안티포달 쌍과 같은 기하학적 배열을 활용하여, 한 차원에 더 많은 특성을 담아내려고 합니다.
요약:
- 이 그래프는 특성들이 숨겨진 차원에 어떻게 표현되는지를 보여주며, 특히 1과 1/2에서 "붙어있는(sticky)" 현상을 강조합니다.
- 밀집한 데이터에서는 하나의 차원이 하나의 특성을 표현하고, 희소한 데이터에서는 안티포달 쌍을 통해 하나의 차원에 두 개의 특성을 표현합니다.
- 이러한 결과는 중첩의 기하학적 구조를 이해하는 데 중요한 통찰을 제공합니다. 모델은 더 많은 특성을 표현하기 위해 공간을 효율적으로 사용하는 전략을 취합니다.

이 그래프는 특성(feature)의 기하학적 구조와 차원성(Dimensionality)을 더 자세히 분석하여, 모델이 학습한 특성들이 어떻게 공간에 배치되는지를 보여줍니다. 특히, 각 특성이 얼마나 많은 차원에 걸쳐 표현되는지와 그 구조가 어떻게 특정한 기하학적 형태를 이룰 수 있는지를 설명합니다.
그래프의 주요 요소:
- X축: 1/(1-S)로, 희소성의 역수를 나타냅니다.
- 왼쪽으로 갈수록 밀집된(dense) 상태, 오른쪽으로 갈수록 희소한(sparse) 상태를 나타냅니다.
- Y축: Feature Dimensionality (D)을 나타내며, 각 특성이 차원에 어떻게 분포되는지를 보여줍니다.
- 예를 들어, Di=1이면 해당 특성은 하나의 차원에 완전히 배정된 상태를 의미합니다. Di=1/2이면 특성이 다른 특성과 안티포달 쌍(antipodal pair)으로 중첩되어 한 차원을 공유하고 있음을 의미합니다.
그래프의 내용:
- 그래프의 주요 부분:
- 윗부분의 그림들: 각 특성들이 어떻게 기하학적으로 배열되는지를 나타냅니다. 각 그림은 특성들의 관계를 나타내며, 이는 특성 간 내적(dot product)에 기반합니다.
- 색상의 의미:
- 빨간색은 특성이 학습되지 않음을 나타냅니다.
- 노란색, 녹색, 파란색, 보라색 등은 각각 특성이 특정 기하학적 구조를 이루며 차원을 공유하는 방식을 나타냅니다.
- 각 라인:
- Dedicated Dimension (1 차원 당 1 특성): 한 차원에 하나의 특성이 완전히 배정되어 독립적으로 표현되는 상태입니다.
- Antipodal Pair (1 차원 당 2 특성): 두 특성이 서로 반대 방향으로 배치되어 한 차원에 중첩되어 표현되는 상태입니다.
- Triangle, Tetrahedron, Pentagon 등: 더 복잡한 기하학적 구조로 특성들이 중첩되어 표현되는 상태를 나타냅니다. 예를 들어, Triangle은 세 개의 특성이 두 차원에서 삼각형 모양으로 배열되는 것을 의미합니다.
- Feature Geometry Graph: 각 특성 노드를 통해 서로 간 내적의 절댓값으로 연결되어 있습니다. 이로써 어떤 특성들이 서로 직교하지 않고 연결되어 있는지를 보여줍니다.
- 특성의 차원성 (Feature Dimensionality):
- 차원성의 정의:
- Di=||Wi||2 / ∑j(Wi⋅Wj)2
- 이 식은 특성 i가 얼마나 잘 표현되는지(분자)와 그 특성이 얼마나 많은 다른 특성과 차원을 공유하는지(분모)를 나타냅니다.
- 차원성의 의미:
- Di=1: 해당 특성이 전용 차원에서 독립적으로 표현됩니다.
- Di=1/2: 안티포달 쌍으로 표현되며, 한 차원에 두 특성이 반대 방향으로 배치되어 중첩됩니다.
- Di=0: 해당 특성이 학습되지 않았음을 의미합니다.
- 차원성의 정의:
- 그래프의 해석:
- 0과 1 사이의 점들: 이 점들은 특성들이 다양한 차원성을 가지며, 중첩(superposition)된 방식으로 표현되고 있음을 보여줍니다. 즉, 중첩은 여러 가지 형태를 가지며, 단순히 하나의 현상이 아닌 다양한 기하학적 구조를 이룰 수 있습니다.
- 특정 부분에 점들이 모이는 현상:
- 예를 들어, Di=1/2에서 점들이 모이는 것은 안티포달 쌍(antipodal pairs)이 효과적인 특성 표현 방식임을 나타냅니다.
- 다른 특정 차원성 값에서도 점들이 모이는데, 이는 모델이 특정 기하학적 구조를 선호하여 특성들을 배열함을 시사합니다.
- 그래프의 주요 발견:
- 중첩의 다양성: 중첩은 단순히 하나의 형태가 아니라 다양한 기하학적 구조를 가지며, 각 특성들이 어떻게 차원에 배치되고 중첩되는지를 보여줍니다.
- 특정 기하학적 구조: 모델은 특성들을 효율적으로 표현하기 위해, 삼각형, 사면체, 오각형과 같은 다양한 구조로 배열합니다.
- Phase Change의 복잡성: 이전에 살펴본 상 변화를 보다 더 복잡하고 세밀하게 보여줍니다. 중첩 내에서도 다양한 하위 단계들이 존재하며, 이는 물리학에서 여러 상이 존재하는 것과 유사합니다.
요약:
- 이 그래프는 특성들의 차원성과 기하학적 구조를 통해, 모델이 어떻게 특성들을 공간에 배치하는지에 대한 더 깊은 이해를 제공합니다.
- 모델은 특성들을 다양한 기하학적 형태로 중첩하여 표현하며, 이는 단순한 상 변화보다 더 복잡한 다단계의 중첩 구조를 보여줍니다.
- 이러한 구조를 이해하면, 모델이 더 많은 특성을 효율적으로 표현하는 방식을 알 수 있습니다.

이 그림은 특성의 기하학적 구조를 이해하기 위해 모델이 어떻게 특정한 다면체(polyhedra) 형태로 특성들을 표현하는지 설명합니다. 특히, 모델이 왜 특정 기하학적 구조를 선택하는지에 대한 이유를 이해하고, 어떻게 이 구조가 테검곱(tegum product)을 통해 형성되는지 설명합니다.
주요 내용:
- 테검곱(Tegum Product):
- 테검곱은 두 개 이상의 다면체를 직교하는 부분공간(orthogonal subspaces)에 임베딩하여 새로운 다면체를 구성하는 방법입니다.
- 이 과정을 통해, 모델은 더 작은 다면체를 결합하여 더 큰 구조를 만들 수 있습니다.
- 세 가지 예시:
- 그림에는 세 가지 예시가 나와 있습니다:
- 삼각 쌍각뿔(Triangular Bipyramid):
- 삼각형과 안티포달 쌍(antipodal pair)의 테검곱으로 구성됩니다.
- 결과적으로 3개의 특성이 2/3의 차원성을 가지며, 2개의 특성이 1/2의 차원성을 가집니다.
- 오각 쌍각뿔(Pentagonal Bipyramid):
- 오각형과 안티포달 쌍의 테검곱으로 구성됩니다.
- 결과적으로 5개의 특성이 2/5의 차원성을 가지며, 2개의 특성이 1/2의 차원성을 가집니다.
- 정팔면체(Octahedron):
- 세 개의 안티포달 쌍의 테검곱으로 구성됩니다.
- 이 경우, 각 특성은 1/2의 차원성을 가지며, 이는 우리가 이미 관찰한 내용과 일치합니다.
- 삼각 쌍각뿔(Triangular Bipyramid):
- 그림에는 세 가지 예시가 나와 있습니다:
- 차원성의 결정:
- 차원성(Dimensionality)이란 특성들이 얼마나 많은 차원에 걸쳐 표현되는지를 나타냅니다.
- 테검곱을 통해 만들어진 구조는 각 다면체의 차원성을 유지하면서 더 큰 구조로 결합됩니다.
- 예를 들어, 삼각형이 2/3의 차원성을 가지는 이유는 삼각형이 2차원에서 3개의 꼭짓점을 가지고 있어 각각의 꼭짓점이 2/3의 차원성을 차지하기 때문입니다.
- 안티포달 쌍은 하나의 차원에 두 개의 반대 방향 특성을 가지므로 각각 1/2의 차원성을 가집니다.
- 테검곱의 중요성:
- 테검곱은 모델이 특성 간 간섭(interference)을 최소화하면서도 많은 특성을 표현할 수 있도록 도와줍니다.
- 직교하는 부분공간에서 두 다면체가 결합되기 때문에, 한 다면체의 특성이 다른 다면체의 특성과 간섭하지 않습니다. 이는 중첩을 최적화하는 데 도움이 됩니다.
- 따라서 모델은 여러 특성들이 동시에 간섭하는 것을 피하기 위해 테검곱 구조를 선호할 수 있습니다.
- 톰슨 문제(Thomson Problem)와의 연관성:
- 톰슨 문제는 구의 표면에 전자들을 배치하는 방법을 다루며, 이러한 배치 방식이 다면체를 형성합니다.
- 이 문제의 해답 중 일부는 테검곱을 통해 만들어진 구조입니다.
- 모델이 특성들을 다면체의 형태로 임베딩하는 방식은 이 톰슨 문제의 해답과 유사하며, 이는 특성들이 구의 표면에 균등하게 배치되는 방식으로 이해할 수 있습니다.
요약:
- 테검곱(tegum product)은 모델이 특성들을 다양한 기하학적 구조로 결합하여 표현하는 방식입니다.
- 이를 통해, 모델은 특성 간 간섭을 줄이면서 더 많은 특성을 표현할 수 있습니다.
- 톰슨 문제와 유사하게, 특성들이 구의 표면에 특정한 형태로 배치되며, 이는 중첩을 이해하는 데 중요한 개념입니다.
Aside: Polytopes and Low-Rank Matrices

이 그림은 다면체(polytopes)와 저차원 행렬(low-rank matrices) 사이의 관계를 시각적으로 보여줍니다. 특히, 특성들의 중첩(superposition)이 어떻게 다면체와 연결되는지, 그리고 이를 통해 행렬이 어떻게 구성되는지를 설명합니다.
주요 내용:
- Columns of :
- 각 다면체의 기둥들은 가중치 행렬 W의 열벡터를 나타냅니다.
- W의 열들은 특성들이 m-차원 공간에 어떻게 배치되는지를 보여줍니다.
- 예를 들어, 삼각형(triangle)의 경우 m=3에서 세 개의 벡터가 균등한 각도로 배치되어 삼각형을 형성합니다.
- 정사각형(square)의 경우 m=4에서 네 개의 벡터가 직각으로 배치되어 사각형을 형성합니다.
- WTW as Graph on W:
- 이 그래프는 WTW의 각 요소를 시각화한 것입니다. 즉, 특성 벡터 간 내적을 나타냅니다.
- 점들은 W의 열벡터에 해당하며, 선은 각 열벡터 간의 내적을 나타냅니다.
- 삼각형의 경우, 각 벡터가 다른 두 벡터와 연결되어 삼각형의 모양을 이룹니다.
- 정사각형의 경우, 모든 벡터가 이웃한 벡터와 연결되어 사각형의 모양을 이룹니다.
- WTW as Matrix:
- 이 부분은 WTW 행렬의 요소를 수치적으로 보여줍니다.
- 대각선 요소는 자기 자신과의 내적(즉, 벡터의 크기)이므로 항상 1입니다.
- 비대각선 요소는 벡터 간의 내적을 나타내며, 이 값은 벡터들이 서로 직교하는지 여부를 나타냅니다.
- 예를 들어, 삼각형에서는 -1/2의 값을 가지며, 이는 특성들이 서로 120 각도를 이룬다는 것을 의미합니다.
- Orthogonal Vectors:
- 이 부분은 어떤 벡터들이 W에 의해 표현되지 않는지, 즉 직교하는 방향을 보여줍니다.
- 예를 들어, 삼각형에서는 (1,1,1) 벡터가 직교 방향입니다. 이는 세 특성이 균등하게 공간을 분할함을 의미합니다.
- 정사각형의 경우, 두 개의 직교 벡터 (1,0,1,0)과 (0,1,0,1)이 존재하며, 이는 네 개의 특성이 두 개의 서로 직교하는 공간에서 균등하게 배치됨을 의미합니다.
그림의 주요 발견:
- 다면체와 행렬의 대응 관계:
- 이 그림은 다면체의 구조가 행렬의 구조와 어떻게 직접적으로 연관되는지 보여줍니다.
- 다면체는 특성들의 기하학적 배치에 해당하며, 이는 행렬의 내적 관계를 통해 수치적으로 표현됩니다.
- 최소 중첩(Minimal Superposition):
- 만약 모든 특성들이 균등하게 중요하고 희소하다면, 가장 효율적인 중첩 전략은 특성들이 균등하게 분포되는 정다면체(예: 삼각형, 사면체 등)를 형성하는 것입니다.
- 이는 최소 중첩을 의미하며, 이 경우 특성들은 가능한 한 서로 간섭을 최소화하면서 공간을 최적으로 분할합니다.
- 직교성:
- WTW 행렬의 구조는 특성 간의 직교성을 보여줍니다.
- 이는 모델이 특성들을 표현할 때 어떤 방향을 선택하지 않는지를 나타내며, 이는 특성들의 배치를 결정하는 데 중요합니다.
요약:
- 이 그림은 다면체와 저차원 행렬 사이의 관계를 통해, 특성 중첩이 어떻게 이루어지는지에 대한 이해를 제공합니다.
- 특성들은 공간을 최적으로 분할하여 최소 중첩을 이루는 다면체의 형태로 배치되며, 이는 WTW 행렬의 구조를 통해 표현됩니다.
- 이러한 구조는 특성 간 간섭을 최소화하고, 모델이 효율적으로 특성들을 표현할 수 있도록 합니다.
특성(feature)이 m-차원 공간에 배치된다는 것은, 모델이 학습하는 각 특성을 -차원 벡터로 표현한다는 의미입니다. 이 벡터들은 모델의 가중치 행렬 W의 열(column)로 나타낼 수 있습니다. 이 개념을 자세히 살펴보겠습니다.
1. 가중치 행렬 W과 특성 벡터:
- 모델이 학습한 가중치 행렬 W의 각 열은 하나의 특성을 나타냅니다.
- 만약 모델이 m개의 숨겨진 차원(hidden dimensions)을 가지고 있다면, 가중치 행렬 은 n * m크기를 가지게 됩니다.
- 여기서 n은 특성의 개수, 은 숨겨진 차원의 수입니다.
- 따라서, 행렬 W의 각 열 벡터는 -차원 공간에서 하나의 특성을 나타냅니다.
2. 특성 벡터의 공간 배치:
- 각 특성은 -차원 공간의 벡터로 표현되며, 이 벡터들은 서로 다른 방향을 가질 수 있습니다.
- 이 벡터들이 공간에 어떻게 배치되는지에 따라 특성 간의 관계가 결정됩니다.
- 예를 들어, 두 특성이 m-차원 공간에서 서로 수직(직교)한다면, 이 두 특성은 서로 간섭하지 않습니다. 그러나 이들이 어떤 각도를 이루고 있다면, 그 각도만큼 서로 간섭할 수 있습니다.
3. WTW 행렬:
- W 행렬의 열 벡터 간의 내적을 계산하면 WTW 행렬을 얻습니다.
- WTW 행렬의 각 요소는 해당 특성 벡터 간의 내적을 나타냅니다.
- 예를 들어, 삼각형 예시에서:
- 행렬 W의 각 열은 삼각형의 꼭짓점을 나타내며, 이 벡터들은 3차원 공간에서 배치됩니다.
- 이 벡터들의 내적은 WTW 행렬의 요소를 형성하며, 이는 특성 간의 관계를 나타냅니다.
4. 특성의 공간적 해석:
- -차원 공간에서 특성 배치:
- 모델은 특성들을 m-차원 공간에 배치하여 표현합니다. 이 공간에서 각 특성은 벡터로 나타나며, 이 벡터들이 이루는 각도와 방향은 특성 간의 관계를 나타냅니다.
- 예를 들어, 만약 모델이 삼각형의 형태로 세 개의 특성을 표현한다면, 이 특성들은 서로 균등한 각도(120도)로 배치됩니다. 이는 이들이 균등하게 공간을 차지한다는 것을 의미합니다.
- 직교성과 간섭:
- 특성 벡터들이 서로 직교한다는 것은 그 특성들이 서로 간섭하지 않고 독립적이라는 것을 의미합니다.
- 만약 특성 벡터들이 직교하지 않는다면, 이들은 서로 간섭하게 됩니다. 이는 WTW 행렬의 비대각선 요소들이 0이 아닌 값을 가질 때 나타납니다.
5. 특성의 중첩 (Superposition)과 다면체:
- 모델은 특성들을 최적으로 표현하기 위해 이들을 m-차원 공간에 다면체(예: 삼각형, 사각형 등)의 형태로 배치합니다.
- 다면체의 각 꼭짓점은 특성 벡터에 해당하며, 이러한 배치는 공간을 최적으로 사용하면서 간섭을 최소화하기 위한 전략입니다.
- 예를 들어, 사각형은 두 개의 안티포달 쌍(antipodal pairs)로 분해될 수 있고, 이는 하나의 차원에 두 개의 특성을 중첩하여 표현하는 방식이 됩니다.
요약:
- 특성의 m-차원 배치: 모델은 각 특성을 -차원 공간의 벡터로 표현하며, 이 벡터들이 공간에 어떻게 배치되는지가 특성 간의 관계를 결정합니다.
- 가중치 행렬 W: 이 행렬의 열은 특성 벡터를 나타내며, 이 벡터들 간의 내적을 통해 특성들의 공간적 관계를 알 수 있습니다.
- 공간적 구조와 중첩: 특성들은 다면체의 형태로 배치되어, 공간을 최적으로 사용하면서 간섭을 최소화합니다. 이는 중첩(superposition)을 효율적으로 수행하는 방법입니다.
이렇게 특성들이 m-차원 공간에 배치됨으로써 모델은 다양한 특성들을 효율적으로 표현하고 처리할 수 있게 됩니다.
중요도가 비슷하다면 정 다면체와 같은 모습을 하여 모든 벡터의 각도를 비슷하게 유지한다.
Non-Uniform Superposition
이 부분에서는 비균일 중첩(Non-Uniform Superposition)에 대해 설명하고 있습니다. 이전에는 모든 특성이 동일한 중요도와 희소성을 가지고 있다고 가정했지만, 실제 상황에서는 특성들이 서로 다를 수 있습니다. 즉, 특성들의 중요도나 희소성이 다르거나 상호 간의 상관 관계가 있는 경우를 고려합니다.
주요 내용:
- 비균일 중첩의 의미:
- 균일 중첩(Uniform Superposition): 이전에 다뤘던 균일 중첩에서는 모든 특성이 동일한 중요도와 희소성을 가지고, 서로 독립적이라고 가정했습니다. 이 경우, 특성들은 최적의 기하학적 구조(예: 정다면체)를 형성합니다.
- 비균일 중첩(Non-Uniform Superposition): 실제로는 특성들이 서로 다른 중요도와 희소성을 가질 수 있으며, 상관 관계가 존재할 수 있습니다. 이런 상황에서는 특성들의 기하학적 구조가 왜곡되고, 새로운 패턴이 나타날 수 있습니다.
- 비균일 중첩에서 나타나는 현상:
- 중요도나 희소성의 변화:
- 특성들이 서로 다른 중요도나 희소성을 가지게 되면, 정다면체 구조에서 점진적으로 변형되기 시작합니다.
- 이러한 변형은 어느 정도 균형을 이루다가, 특정한 임계점에 도달하면 갑작스럽게 다른 기하학적 구조로 전환됩니다.
- 상관된 특성:
- 상관된 특성들은 서로 직교하는 것을 선호합니다. 이 경우, 상관된 특성들은 서로 다른 테검 팩터(tegum factors)에 배치될 수 있습니다.
- 만약 직교할 수 없다면, 이들은 나란히(side-by-side) 배치되는 것을 선호합니다.
- 특정한 경우, 상관된 특성들이 하나의 특성으로 병합될 수도 있습니다. 이는 PCA(주성분 분석)와 유사한 행위와 중첩이 서로 상호작용하는 것처럼 보입니다.
- 반상관된 특성:
- 반상관된 특성들은 같은 테검 팩터에 배치되는 것을 선호하며, 이는 중첩이 필요할 때 나타납니다.
- 이들은 음의 간섭(negative interference)을 가지는 것을 선호하며, 이상적으로는 안티포달(antipodal) 형태로 배치됩니다.
- 중요도나 희소성의 변화:
- 왜 비균일 중첩을 이해해야 하는가?:
- 실제 신경망에서는 특성들이 균일하지 않고, 서로 다른 중요도, 희소성, 상관 관계를 가질 수 있습니다.
- 이러한 비균일 중첩의 기하학적 구조를 이해하면, 모델이 어떻게 더 복잡하고 현실적인 특성들을 표현하는지 알 수 있습니다.
- 현상에 대한 실험적 관찰:
- 다양한 실험을 통해 이러한 현상들을 관찰하고, 비균일 중첩에서 나타나는 패턴을 더 잘 이해할 수 있습니다.
- 이 과정에서, 특성들이 어떻게 기하학적 구조를 이루고, 변형되는지에 대한 새로운 통찰을 얻을 수 있습니다.
요약:
- 비균일 중첩은 특성들이 서로 다른 중요도, 희소성, 상관 관계를 가질 때 나타나는 현상을 설명합니다.
- 이러한 상황에서는 특성들의 기하학적 구조가 변형되고, 새로운 패턴이 나타날 수 있습니다.
- 상관된 특성들은 직교하는 것을 선호하며, 반상관된 특성들은 같은 테검 팩터에서 음의 간섭을 가지는 것을 선호합니다.
- 비균일 중첩을 이해하는 것은 실제 신경망에서 특성들이 어떻게 표현되고 상호작용하는지에 대한 더 깊은 이해를 제공합니다.
Perturbing a Single Feature

이 부분에서는 비균일 중첩(non-uniform superposition)을 이해하기 위해 단일 특성의 희소성(sparsity)을 변경하는 실험을 소개하고 있습니다. 여기서는 5개의 특성을 2차원 공간에 배치하고, 그중 한 특성의 희소성을 조정하면서 전체 구조가 어떻게 변하는지를 관찰합니다.
주요 내용:
- 실험 설정:
- 특성 개수 n=5: 5개의 특성을 가집니다.
- 차원 수 m=2: 이 특성들을 2차원 공간에 배치합니다.
- 균일한 중요도와 희소성: 기본적으로 모든 특성은 동일한 중요도 I=1와 희소성 1-S = 0.05를 가집니다. 이 경우, 특성들은 오각형(pentagon) 모양으로 배치됩니다.
- 단일 특성의 희소성 변경:
- 한 특성의 희소성을 변경하여 더 희소하거나 밀집되도록 합니다.
- 밀집된 경우 (덜 희소):
- 특성이 더 자주 활성화되면(노란색으로 표시), 다른 특성들이 그 특성으로부터 더 멀어지려고 합니다. 이 특성은 더 많은 공간을 차지하게 됩니다.
- 희소한 경우 (더 희소):
- 특성이 덜 자주 활성화되면(파란색으로 표시), 다른 특성들이 이 특성으로 가까이 이동합니다. 이 특성은 덜 공간을 차지하게 됩니다.
- 임계점에서의 변화:
- 특성이 충분히 희소해지면, 오각형이 두 개의 다이곤(digons)으로 분리되는 상 변화(phase change)가 발생합니다.
- 이 시점에서, 희소한 특성은 공간에서 거의 표현되지 않게 되며, 두 개의 다이곤 중 하나가 됩니다.
- 상 변화와 손실 곡선:
- 이 상 변화는 두 가지 다른 기하학적 구조에 대한 손실 곡선이 교차하는 지점과 일치합니다.
- 그림에서 이 손실 곡선의 교차 지점은 페어 오더 상 변화(first-order phase change)임을 보여줍니다.
- 해결 전략:
- 이 실험에서는 해를 표준화(canonicalization)하여 일관된 방식으로 서로 정렬합니다. 이렇게 하면 변형된 특성 배치의 변화를 시각화할 수 있습니다.
- 이 실험을 통해, 비균일 중첩은 균일 중첩의 변형으로 이해될 수 있음을 알 수 있습니다. 즉, 비균일 중첩은 단순히 완전히 다른 상태라기보다는, 균일 중첩 구조 사이에서 변화하는 방식으로 나타날 수 있습니다.
- 오각형이 단위 원에 있지 않은 이유:
- 모델은 양의 간섭(positive interference)을 줄이기 위해 약간의 음의 바이어스(negative bias)를 설정합니다. 이를 통해 노이즈를 차단하고 가중치를 조정합니다.
- 오각형이 단위 원에서 멀리 떨어지는 정도는 주로 양의 간섭의 양에 의해 결정됩니다.
- 재현을 위한 참고사항:
- 2차원 숨겨진 공간에서 최적화하는 것은 연구를 용이하게 하지만, 실제로는 경사하강법(gradient descent)을 사용하여 최적의 결과를 얻는 것이 어렵습니다.
- 여러 번의 시도 후 손실이 가장 낮은 해를 선택하여 이 실험을 진행하였고, 이는 다양한 기하학적 구조에서의 손실 곡선을 관찰하고 상 변화를 이해하는 데 도움이 되었습니다.
요약:
- 이 실험은 단일 특성의 희소성을 변경하여 비균일 중첩이 어떻게 작동하는지 보여줍니다.
- 특성의 희소성이 변할 때, 다른 특성들의 공간 배치가 변화하고, 상 변화가 일어날 수 있습니다.
- 이는 비균일 중첩이 균일 중첩의 변형으로 이해될 수 있음을 보여주며, 이러한 변화를 통해 특성 간의 복잡한 상호작용을 이해할 수 있습니다.
중요도, sparsity가 달라질 수록 loss를 줄이기 위해 중요도가 높은 feature를 확실히 잡아 낼 것이고, 그렇게 진행함에 따라 상 변화가 일어난다!
Correlated and Anticorrelated Features
이 부분에서는 상관된 특성(correlated features)과 반상관된 특성(anticorrelated features)이 있는 상황에서 비균일 중첩(non-uniform superposition)이 어떻게 작동하는지에 대해 설명하고 있습니다. 이는 실제 신경망에서 많은 특성들이 서로 상관관계가 있거나 반상관관계가 있기 때문에, 이들 간의 관계를 이해하는 것이 중요하다는 것을 강조합니다.
주요 내용:
- 상관된 특성과 반상관된 특성:
- 상관된 특성(Correlated Features): 두 특성이 서로 연관되어 있을 때, 즉 한 특성의 값이 높으면 다른 특성의 값도 높아지는 경향이 있는 경우를 말합니다.
- 반상관된 특성(Anticorrelated Features): 두 특성이 서로 반대 방향으로 연관되어 있을 때, 즉 한 특성의 값이 높으면 다른 특성의 값이 낮아지는 경향이 있는 경우를 말합니다.
- 실제 세계의 상관구조:
- 실제 신경망에서는 많은 특성들이 서로 상관관계나 반상관관계를 가지기 때문에, 중첩이 단순히 랜덤하게 일어나지 않습니다.
- 이러한 상관구조는 중첩된 특성들이 어떻게 그룹화되는지를 강하게 결정합니다.
- 상관된 특성의 선호 순위:
- 모델이 상관된 특성을 다루는 방식에는 일종의 선호도가 있습니다:
- 직교 표현: 가장 이상적인 경우, 상관된 특성들은 서로 직교하는 방향으로 표현됩니다. 이 경우, 특성들은 서로 다른 테검 팩터(tegum factors)에 배치되어 서로 간섭하지 않습니다.
- 근접 배치: 직교 표현이 불가능할 때, 모델은 상관된 특성들을 가능한 한 가까이 배치하려고 합니다. 이 경우, 상관된 특성들 간에 양의 간섭(positive interference)이 발생하는 것을 선호합니다.
- 주성분 표현: 공간이 부족하여 모든 상관된 특성을 표현할 수 없을 때, 모델은 이들을 병합하고 주성분(Principal Component)을 대신 표현합니다.
- 이런 순서로 모델은 상관된 특성들을 표현하려고 합니다.
- 모델이 상관된 특성을 다루는 방식에는 일종의 선호도가 있습니다:
- 반상관된 특성:
- 반대로, 반상관된 특성의 경우 모델은 이들이 서로 간섭하는 것을 선호합니다. 특히, 음의 간섭(negative interference)을 선호하며, 이는 두 특성이 서로 반대 방향으로 작용하는 것을 의미합니다.
- 모델이 특성들을 그룹화하는 방법:
- 특성들 간의 상관관계는 중첩된 특성들이 어떻게 그룹화되는지를 결정합니다.
- 만약 상관된 특성들을 그룹화하는 방식이 모델마다 랜덤하다면, 이를 통해 다의성 뉴런(polysemantic neuron)을 식별할 수 있습니다. 그러나 실제로는 상관관계가 모델이 특성을 그룹화하는 방식을 강하게 결정합니다.
요약:
- 상관된 특성과 반상관된 특성의 관계는 중첩된 특성들이 어떻게 배치되고 그룹화되는지를 결정하는 중요한 요소입니다.
- 모델은 상관된 특성들을 다루는 데 선호 순위를 가지고 있으며, 이 순위는 직교 표현 → 근접 배치 → 주성분 표현의 순서로 나타납니다.
- 반상관된 특성은 음의 간섭을 통해 표현하는 것을 선호합니다.
- 이러한 특성들 간의 상관구조는 실제 신경망에서 중첩을 이해하고 예측하는 데 중요한 역할을 합니다.
이러한 관점에서, 상관관계와 반상관관계는 모델이 특성을 효율적으로 표현하고 처리하는 방식에 대한 깊은 통찰을 제공합니다. 이로써 모델이 특성들을 어떻게 그룹화하고 상호작용하는지 이해할 수 있게 됩니다.
관련 있는 것 끼리 묶어놓고, 반대되는 특성은 확실히 반대로 둬서 구분을 둔다.
Setup for Exploring Correlated and Anticorrelated Features
이 부분에서는 상관된 특성 집합(correlated feature sets)과 반상관된 특성 집합(anticorrelated feature sets)을 어떻게 구성하고 탐색할 것인지에 대한 설정을 설명하고 있습니다. 이러한 설정은 특성 간의 관계가 모델의 학습과 표현 방식에 어떻게 영향을 미치는지 이해하는 데 중요한 역할을 합니다.
주요 내용:
- 상관된 특성 집합 (Correlated Feature Sets):
- 개념: 상관된 특성 집합은 함께 발생하는 경향이 있는 특성들의 그룹을 말합니다. 예를 들어, 이미지 분류기에서 동물을 인식하는데 도움이 되는 특성들(털, 귀, 눈)과 건물을 인식하는 특성들(모서리, 창문, 문)이 각각의 집합을 이룰 수 있습니다.
- 수학적 표현:
- 이러한 상관된 특성들은 같은 상황에서 함께 나타나는 경향이 있습니다.
- 이를 수학적으로 모델링하기 위해, 상관된 특성들이 모두 0인지 아닌지를 함께 결정합니다.
- 즉, 특정 확률 S에 따라 이 집합의 모든 특성들이 0이 되거나, 그렇지 않다면 [0,1] 범위 내의 임의의 값으로 활성화됩니다.
- 반상관된 특성 집합 (Anticorrelated Feature Sets):
- 개념: 반상관된 특성 집합은 함께 발생할 가능성이 매우 낮은 특성들의 그룹을 의미합니다. 예를 들어, 특정 이미지에서 어떤 특성이 나타나면 다른 특성은 거의 나타나지 않는 경우를 생각할 수 있습니다.
- 수학적 표현:
- 반상관된 특성 집합에서는 한 번에 하나의 특성만 활성화될 수 있습니다.
- 이 집합이 활성화될 때, 특정 확률 S에 따라 모든 특성들이 0이 되거나, 그 중 하나의 특성만 [0,1] 범위 내의 임의의 값으로 활성화됩니다. 나머지 특성들은 모두 0이 됩니다.
- 이렇게 함으로써, 이 집합의 특성들이 함께 나타날 가능성을 배제하고 반상관 구조를 형성합니다.
실험의 목표:
- 이러한 설정을 통해, 상관된 특성들이 어떻게 한 번에 함께 나타나며 모델의 표현에 영향을 미치는지, 그리고 반대로 반상관된 특성들이 어떻게 서로 배타적으로 나타나는지를 연구할 수 있습니다.
- 이를 통해 모델이 다양한 특성 간의 관계를 어떻게 다루고 표현하는지, 그리고 이 관계가 모델의 학습과 중첩(superposition)에 어떤 영향을 미치는지에 대한 통찰을 얻을 수 있습니다.
요약:
- 상관된 특성 집합은 함께 나타나는 경향이 있는 특성들의 그룹으로, 모델에서 이들의 동시 출현을 모방하도록 설계됩니다.
- 반상관된 특성 집합은 한 번에 하나의 특성만 활성화될 수 있는 그룹으로, 다른 특성이 활성화될 때 이 특성은 나타나지 않습니다.
- 이러한 설정은 특성 간의 관계를 모델링하고, 모델이 이 관계를 통해 어떻게 학습하고 표현하는지 이해하는 데 도움을 줍니다.
이를 통해, 실제 신경망에서 상관된 특성과 반상관된 특성들이 어떻게 표현되고 상호작용하는지 더 깊이 이해할 수 있습니다.
Organization of Correlated and Anticorrelated Features

이 부분에서는 상관된 특성(correlated features)과 반상관된 특성(anticorrelated features)이 2차원 공간에서 어떻게 표현되는지를 관찰하기 위해 여러 작은 장난감 모델을 학습시킨 결과를 설명하고 있습니다. 이 실험에서는 특성들이 어떻게 공간에서 배치되는지 시각적으로 표현하고 비교합니다.
주요 내용:
- 실험 설정:
- 이 실험에서는 2차원 공간(m=2)에서 특성들을 표현하고 그 결과를 시각화합니다.
- 특성들이 어떻게 공간에서 배치되는지 명확하게 보여주기 위해, 해들을 2차원 단위 원 위의 점들로 나타냅니다.
- 또한, 해들을 서로 비교하기 쉽게 하기 위해 회전 및 반전하여 정렬합니다.
- 상관된 특성의 표현:
- 상관된 특성 집합에서는 두 개의 상관된 특성 세트가 서로 직교하는 방향으로 배치되는 경향이 있습니다.
- 그림에서 파란색과 빨간색으로 표시된 특성들은 서로 직교하여 배치되어 있습니다. 이는 모델이 상관된 특성들을 서로 간섭하지 않도록 하기 위한 전략입니다.
- 즉, 상관된 특성들은 서로 나타나는 경향이 있으므로, 이들을 직교하는 방향으로 배치하여 각 특성이 독립적으로 표현될 수 있도록 합니다.
- 반상관된 특성의 표현:
- 반상관된 특성 집합에서는 두 개의 반상관된 특성 세트가 서로 반대 방향으로 배치되는 경향이 있습니다.
- 그림에서 파란색과 빨간색으로 표시된 반상관된 특성들은 서로 반대 방향으로 배치되어 있습니다. 이는 모델이 반상관된 특성들 사이에 음의 간섭을 극대화하여 하나의 특성이 활성화될 때 다른 특성이 나타나지 않도록 하는 전략입니다.
- 즉, 반상관된 특성들은 서로 나타나지 않도록 반대 방향으로 배치되어, 한 특성이 나타날 때 다른 특성이 억제됩니다.
- 상관된 특성이 직교할 수 없는 경우:
- 상관된 특성들을 배치하는 데 충분한 공간이 없는 경우, 특성들이 나란히 배치되는 것을 볼 수 있습니다.
- 그림에서 세 번째 줄의 그림은 세 가지 상관된 특성 세트가 각기 다른 방향으로 배치되어 있는 것을 보여줍니다. 각 색상의 점들은 상관된 특성 집합을 나타내며, 이들은 가능한 한 서로 가까이 배치되어 있습니다.
- 이 상황에서는 특성들이 서로 간섭할 가능성이 있지만, 이는 모델이 모든 상관된 특성을 표현할 수 있는 공간이 부족할 때의 전략입니다.
- 특성들의 "붕괴":
- 때때로 상관된 특성 집합이 "붕괴"하는 경우를 볼 수 있습니다. 이는 최적화 실패의 일환이지만, 특성 간의 관계를 이해하는 데 중요한 현상으로 볼 수 있습니다.
요약:
- 이 실험에서는 상관된 특성들과 반상관된 특성들이 모델에서 어떻게 표현되는지를 시각화했습니다.
- 상관된 특성들은 서로 간섭하지 않도록 직교하는 방향으로 배치되는 경향이 있으며, 반상관된 특성들은 반대 방향으로 배치되어 음의 간섭을 통해 하나의 특성이 활성화될 때 다른 특성이 나타나지 않도록 합니다.
- 이 배치 전략은 모델이 특성 간의 관계를 효율적으로 표현하고 처리하는 방식을 보여줍니다.
이러한 관찰은 모델이 실제 데이터에서 다양한 특성 간의 관계를 어떻게 이해하고 표현하는지에 대한 깊은 통찰을 제공합니다.
Local Almost-Orthogonal Bases

이 부분에서는 상관된 특성들이 로컬 거의 직교 기저(local almost-orthogonal basis)를 형성하는 현상을 설명하고 있습니다. 이 현상은 모델이 특성들을 표현할 때, 상관된 특성들이 서로 간섭하지 않도록 특정 구조를 형성한다는 것을 보여줍니다.
주요 내용:
- 로컬 거의 직교 기저 (Local Almost-Orthogonal Basis):
- 모델이 상관된 특성들을 표현할 때, 이 특성들을 직교하는 방향으로 배치하는 경향이 있습니다.
- 이 현상은 모델 전체가 중첩(superposition) 상태에 있을 때에도 나타나며, 로컬 영역에서 상관된 특성들이 거의 직교하는 기저를 형성하는 것입니다.
- 즉, 전체적으로는 중첩이 일어나지만, 상관된 특성들의 집합 내에서는 거의 직교하는 구조를 가지게 됩니다.
- 실험 설정:
- 두 개의 상관된 특성 집합으로 이루어진 모델을 학습시킵니다. 각 집합은 10개의 상관된 특성들로 구성되어 있으며, 총 20개의 특성이 n=20, 은닉 차원은 m=10입니다.
- 이 모델에서 가중치 행렬 WTW를 시각화하여 상관된 특성들이 어떻게 표현되는지 관찰합니다.
- 시각화 결과:
- 위 그림은 가중치 행렬 WTW를 시각화한 것으로, 색상이 가중치 요소의 값을 나타냅니다.
- 그림에서 각 상관된 특성 집합이 로컬 거의 직교 기저를 형성하고 있음을 볼 수 있습니다.
- 행렬의 대각선 부분은 상관된 특성 집합 내의 특성들이 서로 직교하는 방향으로 배치되어 있음을 보여줍니다.
- WTW의 각 블록은 각 상관된 특성 집합을 나타내며, 이들은 서로 거의 직교하고 있음을 알 수 있습니다. 이는 상관된 특성 집합 내에서 중첩이 거의 일어나지 않음을 의미합니다.
- 의의:
- 만약 이 현상이 실제 신경망에서도 나타난다면, 특정 부분 분포(sub-distribution)에서 활성화되는 특성들이 중첩되지 않는다는 가정을 할 수 있을 것입니다.
- 이는 우리가 주성분 분석(PCA)과 같은 방법을 더 확신을 가지고 사용할 수 있다는 의미입니다. 일반적으로 중첩 상황에서는 PCA를 사용하는 것이 원칙적으로 적절하지 않을 수 있지만, 로컬 거의 직교 기저가 있다면 이 방법을 사용해 특성들을 분석할 수 있는 근거가 됩니다.
요약:
- 상관된 특성들은 모델 내에서 로컬 거의 직교 기저를 형성하는 경향이 있습니다. 이는 모델 전체가 중첩 상태에 있더라도, 상관된 특성들의 집합 내에서는 특성들이 서로 거의 직교하여 표현된다는 것을 의미합니다.
- 이 현상은 특정 부분 분포에서 활성화되는 특성들이 중첩되지 않는다는 가정을 가능하게 하며, 이를 통해 PCA와 같은 분석 방법을 더 확신 있게 사용할 수 있는 근거를 제공합니다.
이러한 관찰은 신경망이 상관된 특성들을 효율적으로 표현하는 방법에 대한 중요한 통찰을 제공하며, 모델의 해석 가능성을 높이는 데 도움을 줍니다.
Collapsing of Correlated Features
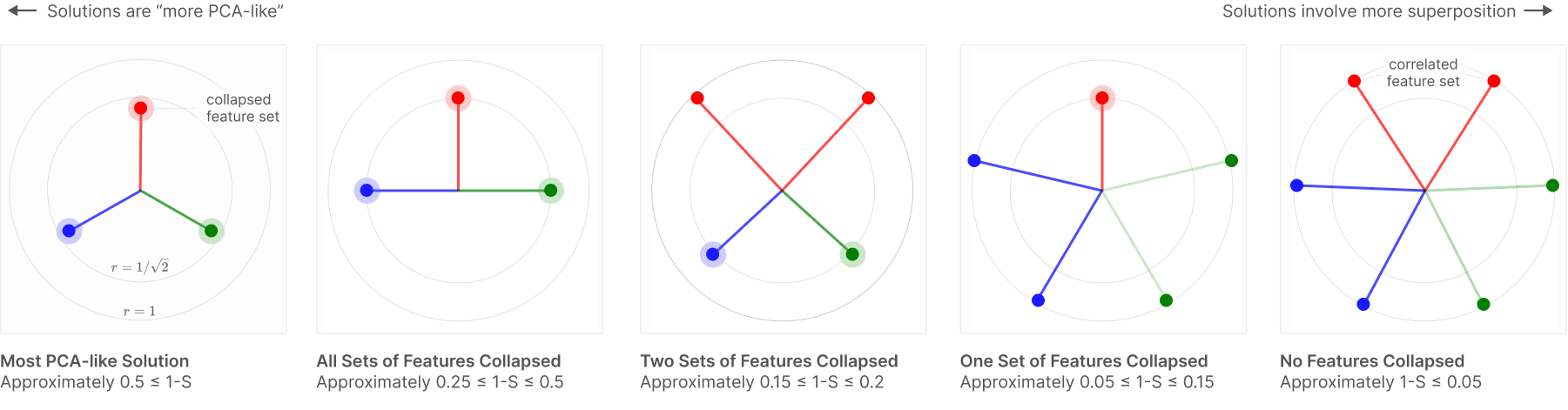
이 부분에서는 상관된 특성들이 모델의 용량 제약으로 인해 주성분(Principal Component)으로 "붕괴"되는 현상을 설명하고 있습니다. 이 현상은 주성분 분석(PCA)과 중첩(superposition) 사이의 상호작용을 보여주며, 모델이 특성들을 표현하는 방식에 대한 통찰을 제공합니다.
주요 내용:
- 상관된 특성의 붕괴:
- 모델이 두 상관된 특성 와 b를 표현할 수 있는 용량이 충분하지 않을 때, 모델은 이 특성들의 주성분(Principal Component)을 표현하는 경향이 있습니다.
- 이때 모델은 두 특성의 주성분인 (a+b)/2를 표현하고, 두 번째 주성분인 (a−b)/2는 무시합니다.
- 이렇게 표현된 주성분은 희소(sparse)하며, 개별 특성보다 손실에 더 큰 영향을 미치게 됩니다.
- 실험 설정:
- 이 실험에서는 6개의 특성이 세 개의 상관된 쌍으로 구성되어 있습니다. 각각의 상관된 쌍은 서로 다른 색상(빨강, 초록, 파랑)으로 표시됩니다.
- 이 상관은 각 쌍의 특성들이 항상 함께 활성화되는 것으로 만들어집니다. 즉, 두 특성 모두 0이거나 둘 다 0이 아닌 값이 됩니다. (활성화될 때의 정확한 비-0 값은 상관되지 않음)
- 희소성의 변화에 따른 특성 표현:
- 특성들의 희소성을 조정하면, 매우 희소한 경우에는 중첩이 발생하며, 특성들이 육각형으로 배열되고 상관된 특성들이 나란히 배치됩니다.
- 반면 희소성이 감소할수록 특성들은 주성분으로 "붕괴"됩니다. 매우 밀집된 경우, 해는 PCA와 동등해집니다.
- 이러한 변화는 희소성과 PCA 사이의 상호작용을 보여줍니다. 즉, 특성들이 더욱 상관될수록 PCA가 더 나은 전략이 되고, 특성들이 희소할수록 중첩이 더 나은 전략이 됩니다.
- 시각화 내용:
- 왼쪽에서 오른쪽으로 가면서 특성들이 "더 PCA에 가까운" 솔루션에서 "더 많은 중첩을 포함하는" 솔루션으로 변화합니다.
- 첫 번째 그림은 가장 "PCA에 가까운" 솔루션을 보여주며, 각 상관된 특성 쌍이 주성분으로 표현됩니다.
- 두 번째 그림은 모든 특성 쌍이 주성분으로 "붕괴"된 경우를 보여줍니다.
- 세 번째와 네 번째 그림은 특성 쌍 중 일부만이 "붕괴"된 경우를 보여줍니다.
- 마지막 그림은 희소성이 높아짐에 따라 중첩이 증가하는 것을 보여줍니다. 특성들이 육각형으로 배열되어 상관된 특성들이 나란히 배치됩니다.
- 의의:
- 이 결과는 PCA와 중첩이 상호 보완적인 전략임을 시사합니다. 특성들이 더욱 상관될수록 PCA가 더 나은 전략이 되고, 특성들이 희소할수록 중첩이 더 나은 전략이 됩니다.
- 실제 신경망에서 특성들이 희소하고 상관될 때, 이 두 전략의 혼합이 발생할 수 있음을 보여줍니다.
요약:
- 상관된 특성들이 모델의 용량 제약으로 인해 주성분으로 "붕괴"되는 현상을 관찰했습니다.
- PCA와 중첩이 특성 표현에 있어 상호 보완적인 전략으로 작동하며, 특성의 희소성과 상관성에 따라 그 활용도가 달라집니다.
- 이 현상은 실제 모델에서 특성들이 어떻게 표현되고 처리되는지에 대한 중요한 통찰을 제공합니다.
Superposition and Learning Dynamics
이 부분에서는 중첩(Superposition)과 학습 동태(Learning Dynamics)에 대한 논의가 진행됩니다. 주로 학습 중에 뉴럴 네트워크가 어떻게 중첩을 형성하고 발전시키는지에 대한 간략한 관찰이 소개됩니다.
주요 내용 및 설명
- 중첩과 학습의 중요성:
- 이 논문의 주된 초점은 완전히 학습된 뉴럴 네트워크에서 중첩이 어떻게 작동하는지에 관한 것이지만, 여기서는 간단하게 학습 과정에서 중첩이 어떻게 발전하는지에 대한 호기심을 표현하고 있습니다.
- 완전히 학습된 모델이 수렴하는 방식이나 구조가 복잡하면서도 이해할 수 있는 형태를 가진다는 점에서, 학습 과정에서 중첩의 형성이 중요하다고 언급합니다.
- 학습 동태를 연구하는 이유:
- 중첩이 어떻게 학습되는지 이해하는 것은 몇 가지 이유에서 중요합니다:
- 지리학적 구조의 수렴: 학습이 진행되면서 모델이 단순하지만 비평범한 구조에 수렴합니다. 이것은 최근 뉴럴 네트워크가 학습 중에 형성하는 가중치 구조가 우리가 이해할 수 있는 기하학적 형태를 가질 수 있다는 증거와 관련이 있습니다.
- 이산적인 학습 패턴: 중첩이 다루는 구조는 놀랍게도 이산적입니다. 이는 뉴럴 네트워크의 학습이 연속적이지 않고 예상보다 이산적일 수 있다는 최근의 발견과 일치합니다.
- 해석 가능성에 대한 영향: 중첩은 뉴럴 네트워크의 해석 가능성에 큰 영향을 미칩니다. 학습 중에 중첩이 언제 나타나는지를 이해하는 것은 모델이 해석 가능한지 여부에 대한 중요한 정보를 제공합니다.
- 중첩이 어떻게 학습되는지 이해하는 것은 몇 가지 이유에서 중요합니다:
- 중첩의 등장 시점:
- 학습 중에 중첩이 초기에 나타나는지 또는 학습 후반부에 나타나는지에 대한 질문을 제기합니다.
- 모델이 더 많은 특성을 맞추려고 할 때 중첩이 나타나는 것이 일반적인지, 아니면 이미 학습 초기에 중첩이 나타나는지에 대해 의문을 던집니다.
- 간략한 관찰:
- 논문의 범위 내에서 이 질문들을 깊게 조사하지는 않습니다.
- 대신, 학습 과정에서 중첩과 관련된 몇 가지 눈에 띄는 현상에 대한 간략한 관찰을 제공하고, 더 자세한 조사는 미래 연구의 과제로 남깁니다.
요약
- 이 부분에서는 뉴럴 네트워크가 학습 중에 중첩을 어떻게 형성하고 발전시키는지에 대한 호기심을 제시하고 있습니다.
- 학습 동태를 이해하는 것은 모델의 최종 구조에 대한 이해와 더불어 중첩이 학습 초기에 나타나는지 후반에 나타나는지를 이해하는 데 도움이 됩니다.
- 학습 중에 중첩이 어떻게 나타나는지에 대한 더 자세한 조사는 미래의 연구 과제로 남겨집니다.
이를 통해 뉴럴 네트워크가 학습을 통해 데이터의 특성을 어떻게 효율적으로 표현하는지, 그리고 이러한 표현이 모델의 해석 가능성과 어떠한 관계가 있는지에 대한 깊은 이해를 얻을 수 있습니다.
Phenomenon 1: Discrete "Energy Level" Jumps
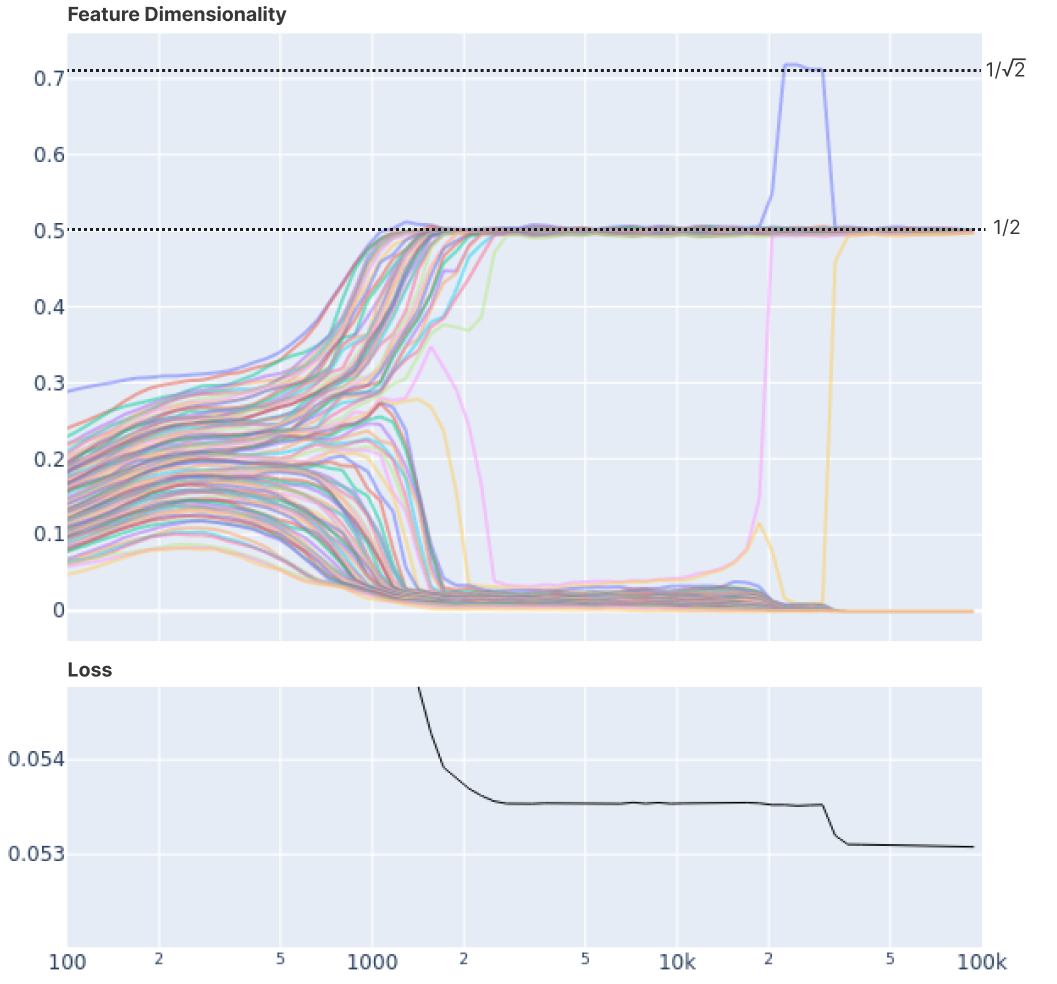
이 부분에서는 뉴럴 네트워크의 학습 과정 중에 나타나는 흥미로운 현상인 "에너지 레벨 점프(Energy Level Jumps)"에 대해 설명합니다. 특히, 이 현상은 중첩(superposition)을 사용하는 모델의 학습 과정에서 관찰됩니다.
단계별 설명
- 에너지 레벨 점프 현상:
- 에너지 레벨 점프는 뉴럴 네트워크가 학습되는 동안, 모델의 특성(feature)들이 특정한 차원 할당 값(Feature Dimensionality) 사이를 갑작스럽게 "점프"하는 현상입니다.
- 여기서 특성의 차원 할당은 각 특성을 표현하는 데 사용되는 차원의 부분을 의미합니다. 즉, 특정 특성을 나타내는 데 얼마나 많은 차원이 사용되는지에 대한 비율을 나타냅니다.
- 학습 세팅:
- 이전 섹션에서 살펴본 것과 같이, 많은 수의 특성이 동등한 중요성과 희소성을 가지는 상황을 고려합니다.
- 최종적으로 이 특성들은 특정 다면체 구조에 자신을 배치하고, 이러한 구조는 특정 차원 할당을 가집니다.
- 특성 차원 할당의 학습 중 변화:
- 첫 번째 그래프에서는 각 색상의 선이 개별 특성의 차원 할당을 나타냅니다.
- 두 번째 그래프는 학습 기간 동안의 손실 함수 값의 변화를 보여줍니다.
- 학습 중에 어떤 특성의 차원 할당이 갑자기 다른 값으로 점프하고, 다른 특성과 위치를 바꾸는 것을 볼 수 있습니다.
- 이 현상이 일어날 때마다, 손실 곡선 또한 갑작스러운 하락을 경험합니다. 이는 첫 번째 점프에서 아주 작고, 두 번째 점프에서 더 큰 하락을 보여줍니다.
- 손실 곡선의 변화:
- 이 그래프에서 볼 수 있듯이, 학습 중에 손실이 감소하는 과정은 실제로는 작은 점프들의 모음입니다.
- 각 점프는 모델이 다른 구성으로 특성을 재배치하는 결과입니다.
- 이러한 점프들은 모델이 최종 구조에 도달하기 전까지 여러 가지 가능한 구조들을 시도하며 학습하고 있음을 나타냅니다.
- 유사한 현상과 관련 연구:
- 이 현상은 Olsson 등의 연구에서 관찰된 유도 헤드의 단계 변화(induction head phase change)와 유사합니다.
- 또한, Nanda와 Lieberum의 연구에서 발견된 모듈러 산술에서의 단계 변화와도 유사합니다.
- 이러한 연구들은 뉴럴 네트워크가 학습 중에 갑작스럽게 기계적 변화를 겪는다는 것을 보여줍니다.
요약
- 에너지 레벨 점프는 뉴럴 네트워크의 학습 과정에서 특성들이 갑작스럽게 다른 차원 할당 값 사이를 이동하는 현상입니다.
- 이 현상은 손실 곡선에 갑작스러운 하락을 유발하며, 이는 모델이 최종 구조에 도달하기 전에 여러 가지 구성들 사이에서 점프하며 학습하고 있음을 나타냅니다.
- 이러한 현상은 뉴럴 네트워크 학습의 동태를 이해하는 데 중요한 통찰을 제공합니다. 특히, 학습이 연속적이기보다 이산적일 수 있다는 증거를 제시합니다.
이를 통해 뉴럴 네트워크가 학습 중에 특성들을 어떻게 조합하고 최적화하는지를 이해할 수 있습니다.
Phenomenon 2: Learning as Geometric Transformations

이 부분에서는 뉴럴 네트워크가 학습되는 과정에서 기하학적 변환(Geometric Transformations)이 어떻게 일어나는지를 설명합니다. 특히, 이 현상은 뉴럴 네트워크가 상관된 특성들을 학습할 때 나타나며, 그 과정은 단순하고 독립적인 기하학적 변환들의 연속으로 이해될 수 있습니다.
단계별 설명
- 기본 설정:
- 이 예시에서는 n=6개의 특성이 m=3개의 숨겨진 차원에서 중첩(superposition)되어 표현되는 문제를 다룹니다.
- 6개의 특성은 2개의 세트로 나뉘며, 각각 3개의 상관된 특성들로 구성되어 있습니다. 이는 이전 섹션에서 설명한 상관된 특성과 연관됩니다.
- 학습 과정 중에 일어나는 변화를 이해하기 위해, 특성 임베딩을 3차원 공간에서 점으로 시각화하여 다면체를 형성하는 과정을 살펴봅니다.
- 학습 단계에 따른 변환:
- A. 초기화 (Weights Initialization):
- 학습 시작 시점에서 가중치는 무작위로 초기화되며, 거의 0에 가깝게 설정됩니다.
- 이는 손실 함수 값이 높게 시작하는 것을 나타냅니다.
- B. 첫 번째 변화 (Push Apart One Axis):
- 학습의 첫 번째 단계에서, 두 세트의 상관된 특성들이 한 축을 따라 서로 밀어내는 현상이 일어납니다.
- 이는 두 세트의 특성들이 서로 다른 방향으로 배치되도록 합니다.
- C. 삼각형으로 확장 (Expanding into a Triangle):
- 다음 단계에서 각 세트의 상관된 특성들이 서로 삼각형을 이루도록 확장됩니다.
- 이 과정에서 특성들은 더 복잡한 구조로 배치되며, 각 세트 내에서의 특성들이 삼각형 형태를 취하게 됩니다.
- D. 최종 형태로 회전 (Rotating into an Antiprism):
- 마지막 단계에서, 삼각형들이 서로 회전하여 안티프리즘(Antiprism) 형태로 배치됩니다.
- 이때, 각 삼각형이 서로 다른 세트의 특성과 대칭적 쌍(Antipodal Pair)을 이루며 배치됩니다.
- A. 초기화 (Weights Initialization):
- 손실 곡선의 변화:
- 아래 손실 곡선 그래프에서 볼 수 있듯이, 학습 과정은 여러 개의 명확한 단계를 거칩니다.
- 각 단계는 가중치의 기하학적 변환과 연관되어 있습니다.
- 손실 값이 급격히 떨어지는 지점은 특성들이 새로운 구조로 재배치되는 순간을 나타냅니다.
- 이전 연구와의 연관성:
- 이러한 학습 동태는 이전 연구의 결과와 직접적으로 연관되어 있습니다. 특히, 두 층 신경망이 학습 초기 단계에서 문제에 대한 선형 근사를 학습하는 경향이 있다는 연구와 유사합니다.
- 이 경우, 모델이 초기에는 선형 PCA 솔루션을 학습한 후에 더 나은 비선형 솔루션으로 이동하는 모습을 보여줍니다.
- 또한, 계층적 특성 집합을 다루는 다른 연구에서는 데이터 생성 과정이 비슷한 문제에서 관찰된 것처럼 특정 네트워크가 임베딩 벡터를 "분할"한다는 것을 발견했습니다.
요약
- 뉴럴 네트워크의 학습은 기하학적 변환의 연속으로 이해될 수 있습니다.
- 특성들이 서로 상관되어 있을 때, 학습 과정은 여러 명확한 단계들을 거치며, 각 단계는 특성들의 새로운 배치를 나타냅니다.
- 이 과정은 선형 근사에서 비선형 솔루션으로의 전환을 보여주며, 이전 연구 결과와 일치하는 모습을 보입니다.
이를 통해 뉴럴 네트워크가 복잡한 특성 구조를 학습하는 방식을 더 깊이 이해할 수 있습니다. 특히, 기하학적 변환을 통해 뉴럴 네트워크가 특성들을 최적화하고 표현하는 과정을 시각적으로 파악할 수 있습니다.
상관된 것 끼리 묶여서 나눠지다가 결국 그 상관된 것 끼리도 점차 거리를 벌려가며 학습하네요
Relationship to Adversarial Robustness

이 부분에서는 슈퍼포지션(superposition)이 모델의 적대적 예제(adversarial examples)에 대한 취약성과 어떻게 관련되어 있는지 설명하고 있습니다. 이 관계는 직관적으로 생각해볼 때 이해가 될 수 있습니다.
슈퍼포지션과 적대적 예제의 관계
- 슈퍼포지션 없는 모델:
- 모델이 슈퍼포지션을 사용하지 않을 때, 첫 번째 특성에 대한 가중치는 간단하게 배치됩니다. 예를 들어, (WTW)0=(1,0,0,0,...)
- 여기서 첫 번째 특성에 대한 가중치가 명확하게 표현되어 있고, 다른 특성들 간의 간섭이 없습니다.
- 슈퍼포지션 있는 모델:
- 슈퍼포지션이 있는 모델에서는, 특성들이 서로 간섭(interference)하게 됩니다. 예를 들면, (WTW)0=(1,ϵ,−ϵ,ϵ,...)
- 여기서 ϵ은 슈퍼포지션 간섭의 아티팩트이며, 이는 가장 중요한 특성을 공격하는 명백한 방법을 제공합니다. 즉, 다른 특성들의 간섭으로 인해 작은 변화에도 영향을 받을 수 있게 됩니다.
- 슈퍼포지션이 적대적 공격에 취약한 이유:
- 슈퍼포지션으로 인해, 모델은 적대적 예제에 취약해집니다. 왜냐하면 간섭으로 인해 다른 특성들이 첫 번째 특성에 영향을 미치기 때문입니다.
- 이 간섭은 무한한 데이터 상황에서도 발생할 수 있는데, 이는 모델이 더 많은 특성을 표현하기 위해 슈퍼포지션을 사용하기 때문입니다.
- 실험 및 관찰:
- 모델이 적대적 공격에 얼마나 취약한지 테스트하기 위해 L2 적대적 예제를 생성했습니다.
- 이 실험에서는 평균 입력 크기의 0.1의 최대 L2 공격 노름을 허용하여 공격을 생성했습니다.
- 분석 결과, 슈퍼포지션이 형성되기 시작할 때부터 적대적 공격에 대한 취약성이 급격히 증가하는 것이 관찰되었습니다.
- 이 취약성은 특성당 차원 수(차원의 역수)와 밀접한 관련이 있음을 발견했습니다.
그래프 설명
- 상단 그래프 (적대적 취약성 증가):
- 슈퍼포지션을 사용하기 시작할 때, 그리고 슈퍼포지션이 더 복잡해질 때 모델의 적대적 예제에 대한 취약성이 어떻게 증가하는지 보여줍니다.
- 슈퍼포지션이 더 많이 사용될수록 (특히 안티포달 슈퍼포지션이 사용되는 경우), 적대적 예제에 대한 취약성은 최대 8배까지 증가합니다.
- 중간 그래프 (특성당 차원 수):
- 여기서는 각 차원당 특성 수를 플롯하며, 이는 이전에 정의한 "차원 수의 역수"를 나타냅니다.
- 이 곡선은 적대적 예제에 대한 취약성의 증가와 유사한 형태를 보여줍니다.
- 하단 그래프 (적대적 취약성 vs 특성당 차원 수):
- 이 그래프는 적대적 취약성을 특성당 차원 수에 대해 직접 플롯한 것입니다.
- 이는 적대적 취약성이 차원당 저장된 특성 수와 높은 상관관계를 갖고 있음을 보여줍니다.
결론
- 슈퍼포지션과 적대적 예제:
- 슈퍼포지션을 사용하면 모델이 적대적 예제에 더 취약해질 수 있습니다. 이는 슈퍼포지션이 특성 간 간섭을 유발하고, 이로 인해 적대적 공격에 더 쉽게 노출되기 때문입니다.
- 적대적 예제를 생성하는 것은 슈퍼포지션을 더 잘 이해하고, 더 강력한 모델을 만들기 위해 중요한 실험입니다.
- 슈퍼포지션의 영향력:
- 슈퍼포지션이 적대적 예제의 주요 원인일 수 있다는 주장이 있을 수 있으며, 이는 더 해석 가능한 모델을 만들기 위해 중요한 요소로 고려될 수 있습니다.
- 그러나 적대적 예제에 대한 다른 이론들도 있으므로 슈퍼포지션이 유일한 원인이라고 단언할 수는 없습니다.
이 연구는 슈퍼포지션이 모델의 적대적 공격에 대한 취약성과 직접적인 연관이 있을 수 있음을 보여주며, 이는 더 해석 가능하고 강력한 모델을 만들기 위해 중요한 인사이트를 제공합니다.
슈퍼포지션(superposition)과 적대적 공격(adversarial attack)에 대해 자세히 설명하겠습니다.
1. 슈퍼포지션(Superposition)
개념
- 슈퍼포지션은 딥러닝 모델이 특성(feature)을 표현할 때 사용하는 방법 중 하나입니다. 모델은 주어진 공간에 많은 특성을 표현하고자 하는데, 그 공간이 제한적이라면 여러 특성을 서로 겹쳐서 표현하려고 합니다.
- 이로 인해 하나의 뉴런(노드) 또는 차원에 여러 특성이 섞여 저장됩니다. 이러한 특성들이 선형 결합(linear combination)의 형태로 표현되는데, 이 상태를 슈퍼포지션이라고 합니다.
- 모델이 슈퍼포지션을 사용하는 이유는 메모리와 표현의 효율성을 높이기 위해서입니다. 하지만 이는 간섭(interference)을 유발할 수 있습니다.
슈퍼포지션의 문제점
- 간섭: 여러 특성이 같은 공간에 표현되면, 이 특성들 사이에 간섭이 발생합니다. 즉, 하나의 특성에 대한 변화가 다른 특성의 표현에도 영향을 줄 수 있게 됩니다.
- 해석의 어려움: 슈퍼포지션으로 인해 한 뉴런이 여러 특성을 동시에 표현할 수 있으므로, 뉴런의 출력을 해석하고 이해하는 것이 더 어려워집니다.
- 적대적 공격에 대한 취약성: 여러 특성이 겹쳐져 있기 때문에, 적대적 공격이 이러한 간섭을 이용해 모델의 출력을 쉽게 교란시킬 수 있습니다.
2. 적대적 공격(Adversarial Attack)
개념
- 적대적 공격은 모델이 예측할 때 작은 노이즈나 변화를 주어 모델이 잘못된 출력을 내도록 유도하는 공격 방법입니다. 이는 모델이 예측을 위해 사용하는 입력의 아주 작은 부분을 변경하는 것입니다.
- 이 작은 변화는 사람 눈에는 거의 구분이 되지 않지만, 모델이 사용하는 복잡한 수학적 구조로 인해 모델의 출력에 큰 영향을 줄 수 있습니다.
적대적 공격의 원리
- 예시: 이미지 분류 모델에 작은 픽셀 변경을 가하여, 사람이 보기에 여전히 고양이 사진이지만 모델이 이를 개로 분류하게 만들 수 있습니다.
- 이러한 공격은 모델의 결정 경계(decision boundary)를 교란시키고, 모델이 오작동하도록 유도합니다.
슈퍼포지션과 적대적 공격의 관계
왜 슈퍼포지션이 적대적 공격에 취약한가?
- 슈퍼포지션은 특성들이 겹쳐 표현되어 있기 때문에, 적대적 공격이 이러한 겹침을 이용할 수 있습니다.
- 슈퍼포지션에서는 뉴런의 가중치에 작은 변화만 주어도 여러 특성에 영향을 줄 수 있습니다.
- 이는 공격자가 모델이 의존하는 특정 특성들에 작은 교란을 주어 모델이 잘못된 결정을 내리도록 유도하는 것을 쉽게 만듭니다.
예시로 설명
- 슈퍼포지션 없는 모델에서는 한 특성이 다음과 같이 표현될 수 있습니다:
(WTW)0=(1,0,0,0,...)여기서는 첫 번째 특성만을 분명하게 표현하고, 다른 특성들과 간섭이 없습니다. - 슈퍼포지션을 사용하는 모델에서는, 한 특성에 대한 표현이 다른 특성들의 영향을 받습니다:
(WTW)0=(1,ϵ,−ϵ,ϵ,...)여기서 ϵ은 다른 특성들이 첫 번째 특성에 미치는 간섭을 나타냅니다. - 공격자는 이 간섭을 이용해 ϵ 값들을 조정하여 모델이 잘못된 예측을 하게 만들 수 있습니다.
적대적 공격 실험과 결과
- 연구에서는 L2 노름을 사용하여 적대적 예제를 생성했습니다. 이를 통해 슈퍼포지션을 사용하는 모델이 더 취약함을 확인했습니다.
- 슈퍼포지션이 적은 모델은 이러한 공격에 비교적 강하지만, 슈퍼포지션이 있는 모델은 간섭 때문에 더 쉽게 공격을 받습니다.
결론
- 슈퍼포지션은 모델이 제한된 자원으로 많은 특성을 표현하려고 할 때 유용하지만, 이는 특성들 간의 간섭을 유발하고, 모델을 적대적 공격에 더 취약하게 만듭니다.
- 적대적 공격은 이러한 간섭을 이용하여 모델의 출력을 교란시키는 방법이며, 슈퍼포지션을 사용하는 모델은 이러한 공격에 더 노출되어 있습니다.
이러한 관계는 딥러닝 모델의 해석 가능성과 신뢰성에 중요한 요소로 작용하며, 슈퍼포지션을 어떻게 처리하느냐에 따라 모델의 강건성(robustness)을 향상시킬 수 있습니다.
한 노드에서 여러 feature를 표현하려다 보니(슈퍼 포지션) 작은 노이즈(적대적 공격)에도 민감하게 출력이 반응한다.
Superposition in a Privileged Basis
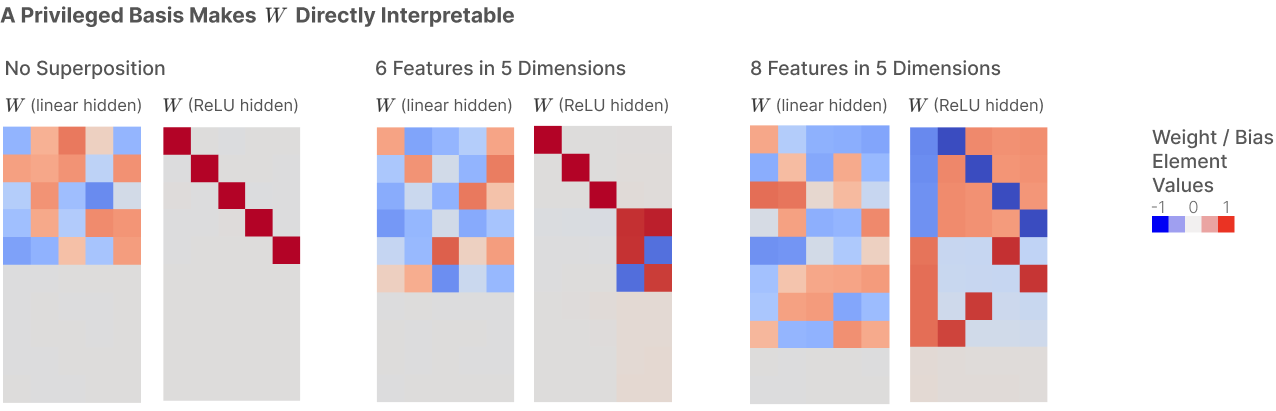
이 부분은 신경망의 가중치 행렬 W의 해석 가능성에 관한 내용입니다.
1. Privileged Basis (특권적 기준):
- 특권적 기준이 없는 경우: 앞서 설명한 것처럼, 네트워크의 은닉층에 대한 표현을 자유롭게 회전(선형 변환)하더라도 네트워크의 동작은 동일합니다. 이는 특정 방향이나 기준이 없다는 것을 의미하며, W의 해석이 어렵게 만듭니다.
- 특권적 기준이 있는 경우: 하지만 우리가 중간 층에 ReLU 같은 활성화 함수를 추가하면 이야기가 달라집니다. ReLU는 뉴런을 특정 기준에 따라 활성화하거나 비활성화하므로, 이 중간층에 특권적 기준을 부여하게 됩니다. 이는 특권적 기준이 있는 네트워크의 경우를 나타내는데, 이러한 경우에는 행렬을 직접 해석할 수 있습니다.
2. ReLU 활성화의 영향:
- ReLU 활성화 함수: 이 함수는 입력이 양수일 때는 그대로 통과시키고, 음수일 때는 0으로 만듭니다. 이것은 네트워크의 표현을 분리하고, 뉴런이 특정 입력 특성에 더 민감하게 반응하도록 만듭니다.
- 가중치 행렬 해석: 특권적 기준을 가진 ReLU 모델에서는 를 해석하는 것이 더 쉽습니다. 왜냐하면 가 각 특성을 뉴런에 직접 연결하고, 일부 뉴런은 단일 특성에 전념하기 때문입니다.
3. 비교:
- No Superposition (슈퍼포지션 없음): 왼쪽 첫 번째 그림은 슈퍼포지션이 없는 경우를 보여줍니다. 여기서 가중치 행렬은 의 각 행과 열이 독립적으로 해석되지 않고 혼합되어 있습니다.
- 6 Features in 5 Dimensions (5차원에 6개의 특성): ReLU 모델에서 특성들이 뉴런에 정렬되어 있고, 몇몇 뉴런들은 특정 특성에 전념하고 있습니다. 즉, 이 뉴런들은 단일 특성을 대표하고 있습니다.
- 8 Features in 5 Dimensions (5차원에 8개의 특성): 이 경우, 뉴런들은 여러 특성을 더 복잡하게 대표하고 있습니다. 그러나 여전히 일부 뉴런들은 특정 특성에 집중하고 있습니다.
이러한 내용은 뉴런 중심의 해석 방법이 어떤 경우에 효과적일 수 있는지 보여줍니다. ReLU와 같은 활성화 함수로 인해 뉴런들이 특정 특성에 정렬되거나 집중하게 되고, 이를 통해 해석이 가능한 모델 구조가 만들어집니다.
한 노드에서 Feature를 많이 담당할 수록 해석하기 어려워지고, 누가 어떤 feature를 집중하는지 모른다.
그래도 ReLU와 같은 activation function을 통해 해석 가능한 모델을 만들 수 있다.
Visualizing Superposition in Terms of Neurons


이 부분에서는 네트워크의 내부 가중치를 시각화하여 뉴런이 어떻게 여러 특성(피처)을 표현하는지 이해하는 방법에 대해 설명하고 있습니다. 이를 통해 슈퍼포지션이 뉴런 수준에서 어떻게 나타나는지, 그리고 뉴런이 어떻게 피처를 표현하는지 알 수 있습니다.
주요 내용 및 단계별 설명
1. W를 행렬로 시각화
- W 행렬은 피처에서 뉴런으로 가는 가중치를 나타냅니다. 각 행은 뉴런과 연결된 피처를, 각 열은 특정 뉴런에 대한 가중치를 나타냅니다.
- W 행렬을 시각화함으로써 어떤 뉴런이 특정 피처를 강하게 나타내는지, 즉 특정 피처에 대해 높은 가중치를 갖는지 확인할 수 있습니다.
- 이 행렬을 보면, 일부 뉴런은 한 가지 피처에만 높은 가중치를 가지는데, 이러한 뉴런을 모노세만틱 뉴런이라고 부릅니다.
2. 스택 플롯으로 W 시각화
- 각 뉴런이 어떤 피처를 얼마나 표현하는지 쉽게 보기 위해 스택 플롯을 사용합니다.
- 스택 플롯에서는 각 뉴런이 얼마나 많은 피처를 표현하는지 시각적으로 보여줍니다. 각 막대의 높이는 가중치의 크기를, 색상은 해당 가중치가 어떤 피처를 나타내는지를 나타냅니다.
- 여러 피처를 동시에 나타내는 뉴런을 폴리세만틱 뉴런이라고 합니다.
3. 희소성 수준에 따른 뉴런의 변화
- 모노세만틱 뉴런: 모델의 희소성이 낮을 때, 대부분의 뉴런은 각각 하나의 피처를 전담하여 표현합니다. 이 상태를 모노세만틱이라고 합니다.
- 폴리세만틱 뉴런: 희소성이 높아지면, 모델은 뉴런의 수가 한정되어 있기 때문에 하나의 뉴런이 여러 피처를 표현해야 합니다. 이때 뉴런이 여러 피처를 표현할 때 폴리세만틱이 됩니다.
- 예를 들어, 희소성이 0.5에서 1 사이일 때, 모든 뉴런은 모노세만틱이고 각 피처에 대해 전담 뉴런이 있습니다.
- 희소성이 증가함에 따라 뉴런들이 점차적으로 폴리세만틱해지며, 한 뉴런이 두 개 이상의 피처를 표현하는 경우가 발생합니다.
4. 뉴런이 피처를 표현하는 구조
- 바이너리 코드: 어떤 경우에는 뉴런이 두 개 이상의 피처를 나타내기 위해 일종의 이진 코드를 형성하기도 합니다. 예를 들어, 두 개의 뉴런이 세 개의 피처를 표현하는 경우입니다.
- 특정 코드 구조: 희소성이 증가하면서 뉴런은 특정 피처를 표현하기 위해 점점 더 복잡한 코드 구조를 사용합니다. 예를 들어, 중요한 피처와 중요하지 않은 피처를 구분하는 뉴런이 등장하고, 나머지 뉴런들이 다양한 조합을 통해 피처를 표현합니다.
5. 변화의 중요성
- 이 변화는 모델이 단순히 모든 피처를 독립적으로 표현하는 것이 아니라, 뉴런이 여러 피처를 동시에 표현함으로써 효율적으로 슈퍼포지션을 수행할 수 있음을 보여줍니다.
- 슈퍼포지션은 희소성에 따라 변화하며, 이는 뉴런이 피처를 표현하는 방식에 직접적인 영향을 줍니다.
결론
이러한 시각화와 분석을 통해, 뉴런이 피처를 어떻게 표현하는지, 특히 슈퍼포지션과 관련하여 어떻게 피처를 효율적으로 표현하는지를 이해할 수 있습니다. 희소성이 증가할수록 뉴런은 더욱 복잡한 방식으로 피처를 표현하게 되고, 이는 슈퍼포지션의 핵심 개념을 보여줍니다.
Limitations of The ReLU Hidden Layer Toy Model Simulating Identity
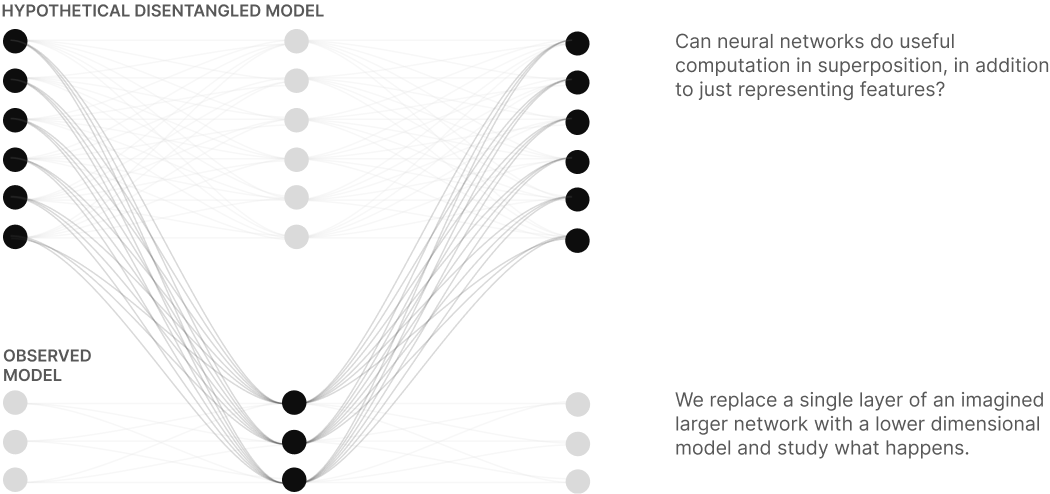
Computation in Superposition
'인공지능 > XAI' 카테고리의 다른 글
| Sae 학습에 따른 dead_features (2) | 2024.10.04 |
|---|---|
| LLama3 학습 데이터 변환하여 LLama3.2 Sparse Autoencoder 학습하기 (3) | 2024.09.27 |
| SAE 통해 특정 feature를 강화시켜 LLM 출력 변형하기 - 미스트랄 mistral 7b (2) | 2024.09.26 |
| SAE Tutorial summarize (4) | 2024.09.24 |
| Sparse Autoencoder 시작 (1) | 2024.09.19 |