2025.09.02 - [인공지능/논문 리뷰 or 진행] - Language Model 파라미터 감소(Pruning) 논문 3
Language Model 파라미터 감소(Pruning) 논문 3
2025.09.02 - [인공지능/논문 리뷰 or 진행] - Language Model 파라미터 감소(Pruning) 논문 2 Language Model 파라미터 감소(Pruning) 논문 22025.08.08 - [인공지능/논문 리뷰 or 진행] - Language Model (LM) Pruning 논문 1 Langua
yoonschallenge.tistory.com
여기에 또 이어져서...
https://arxiv.org/abs/2402.14800
Not All Experts are Equal: Efficient Expert Pruning and Skipping for Mixture-of-Experts Large Language Models
A pivotal advancement in the progress of large language models (LLMs) is the emergence of the Mixture-of-Experts (MoE) LLMs. Compared to traditional LLMs, MoE LLMs can achieve higher performance with fewer parameters, but it is still hard to deploy them du
arxiv.org
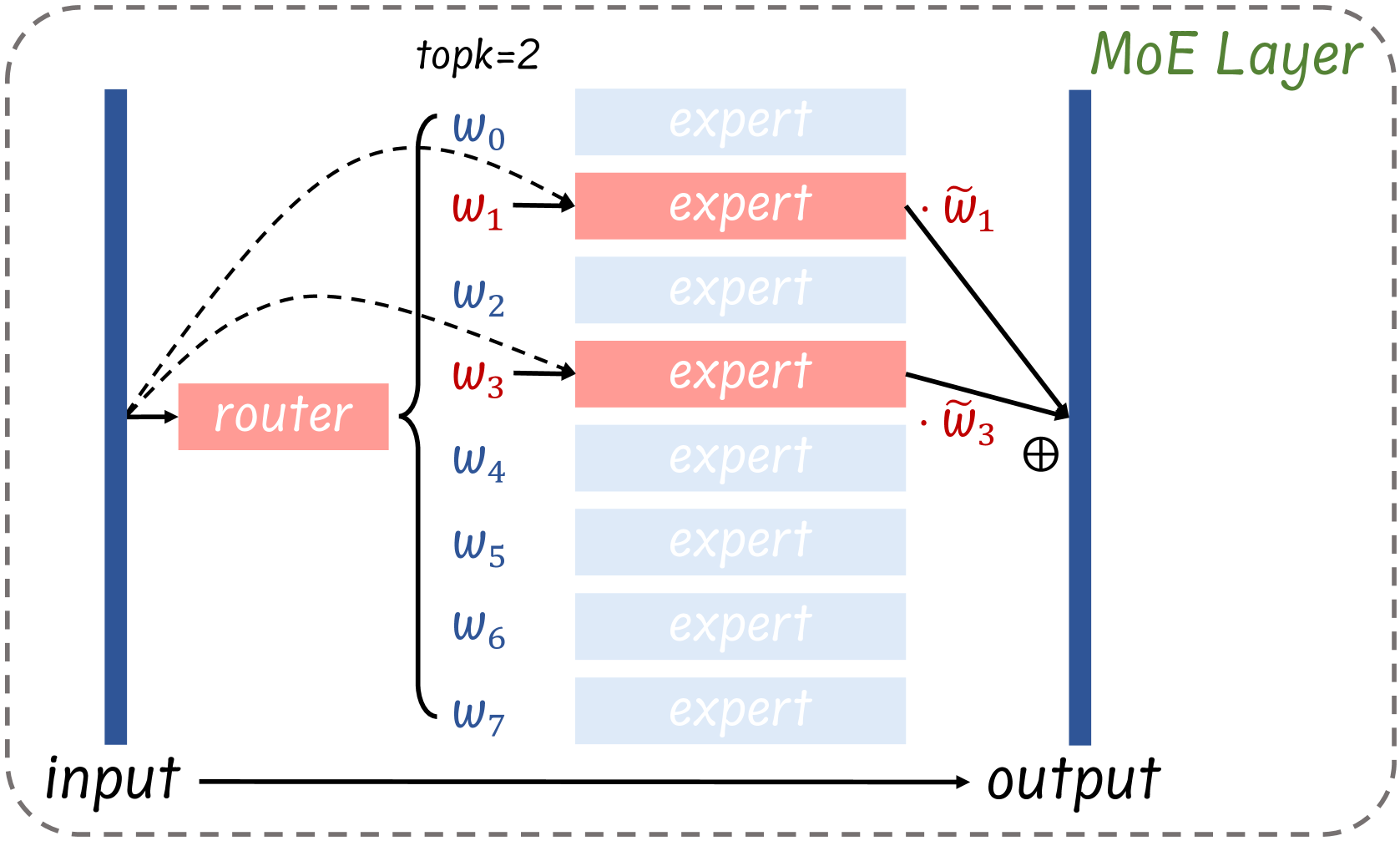
MOE는 모델의 사이즈가 크고, inference할 때 라우팅을 통해 특정 파라미터만 활성화되는 모델입니다.
그러나 안쓰이는 부분이 VRAM 차이 용량이 너무 커서 GPU가 많이 필요하고 이를 위해 Expert를 버리고, 라우팅 시에도 값이 일정 이상 넘지 못하면 한개의 Expert만 연산하여 연산량, 공간 모두 줄였습니다.
| 문제 상황 | MoE LLM은 토큰당 top-k만 활성화되어도 정적 파라미터(전문가 가중치)가 대부분을 차지해 배포가 어렵다. 예: Mixtral-8×7B(bf16) 로딩에 A100-80G 2장 필요, 8명 전문가가 총 파라미터의 ≈96%(45B/47B) 차지. |
| 제안 방법(요약) | 학습 없이 사후(post-training)로 전문가 수준 희소화를 도입: (1) Expert Pruning—층별로 보정셋을 써서 전문가 조합을 열거·평가하여 재구성 손실 최소 조합만 보존, (2) Dynamic Skipping—추론 중 토큰별로 두 번째 전문가를 w2≤βw1조건이면 건너뜀(층별 β = median(w2/w1)). |
| 방법론 세부 – Expert Pruning | (i) 보정셋 구성: 일반 과제는 C4에서 128 시퀀스(각 2048 토큰) 수집, 도메인 과제(수학)는 MATH를 C4 포맷으로 재구성해 동일 방식으로 샘플링. (ii) 캐싱: 원본 MoE로 각 층의 (입력,출력) 토큰쌍 캐시. (iii) 조합 탐색: 각 층에서 n명 중 r명 조합을 열거, ∥F′(x,C)−F(x)∥_F 최소 조합 채택, 나머지 영구 제거. |
| 방법론 세부 – Dynamic Skipping | Mixtral(top-2) 가정에서, 토큰 x의 라우팅 가중치가 w1≥w2일 때 w2<βw1이면 2번째 전문가를 스킵. β는 보정셋으로 층별 median(w2/w1). 일반 top-k로의 오차 상한식도 제시. |
| 실험 설정(데이터·학습법) | 일반 과제: C4 보정셋(128×2048)으로 프루닝 후 LM Harness 8태스크(ARC-c/e, BoolQ, HellaSwag, MMLU, OBQA, RTE, WinoGrande) 제로샷 평가. 도메인(수학): MATH 보정셋으로 r=6/4 프루닝 후 GSM8K 5-shot 평가. 후속 미세튜닝: MetaMathQA로 8/7/6-expert를 900 steps, lr=2e-5, cosine, A100-80G×16. |
| 주요 결과 – 일반 과제 | 프루닝만: r=6 → 1.20× 속도, r=4 → 1.27× 속도(통신 감소 등으로 토큰속도↑). 프루닝+스킵: r=6+skip → 1.27×, r=4+skip → 1.33×. (표5) |
| 주요 결과 – 도메인(수학) | C4로 프루닝하면 수학 성능 급락(GSM8K 5-shot: 58.61 → 41.02 @r=6). MATH로 교체 시 급락 완화, 미세튜닝 뒤 7-expert가 8-expert를 상회하는 경우도 관찰. (표3·표4) |
| 메모리/속도/조합 | 메모리(표9): r=6 76%, r=4 52%(원본 대비), Wanda-2:4는 57%. 결합 효과(표8): 도메인 태스크서 r=6+skip이 r=4 단독과 유사 속도면서 정확도 우위. |
| 비교·분석 | Layer-wise가 Progressive보다 고프루닝(r=4)에서 성능 저하 적음(59.57 vs 57.53). 전문가 선택 분포는 C4 vs MATH가 상이(동일 조합이 4개 층만 일치). |
| 기여 | MoE LLM에 대한 사후 전문가 프루닝/스킵핑을 플러그-앤-플레이로 제안(하드웨어 의존↓), 메모리 절감과 추론 가속을 동시에 달성. 코드 공개 예고. |
| 한계/주의 | (1) 보정셋 정합성: 일반(C4)로 프루닝하면 수학 등 도메인 성능 급락 → 도메인 보정셋 필요. (2) 스킵은 메모리↓ 아님(런타임 FLOPs/속도 개선이 주효과). (3) 조합 탐색 비용: 층당 (nr)\binom{n}{r} 전방패스 필요. |
| 재현 팁 | (a) 보정셋 크기: 64–128 시퀀스(각 2048)에서 안정(표7). (b) β 산정: 층별 median(w_2/w_1). (c) 평가 태스크: LM Harness 8종. (d) 프루닝 후 미세튜닝: MetaMathQA 900 steps, lr=2e-5, cosine. |
다음은 업로드하신 논문 **“Not All Experts are Equal: Efficient Expert Pruning and Skipping for Mixture-of-Experts Large Language Models”**의 한국어 핵심 정리입니다. 연구 맥락–방법–실험–결과–기여–한계를 체계적으로 정리하고, 실전에 바로 쓸 수 있도록 expert pruning/skip 절차를 step-by-step로 제공합니다.
한눈에 핵심
- 문제: MoE LLM(Mixtral 8×7B 등)은 토큰당 top-k 전문가만 활성화해도, 전체 **전문가 파라미터(예: 8개 전문가가 전체의 ≈96%)**가 메모리/배포 병목이 됨. bf16 로딩에도 A100-80G×2가 필요할 정도로 무거움.
- 해결: 학습 없이 사후(post-training) expert-level sparsity를 도입. (1) 전문가 가지치기(pruning): 각 MoE 층에서 보존할 r개 전문가 조합을 열거·평가해 출력 재구성 손실이 최소인 조합만 남김. (2) 동적 스킵핑(dynamic skipping): 토큰별 라우팅 가중치 비율 기준으로 두 번째 전문가를 즉시 생략해 FLOPs/지연을 추가로 절감.
- 효과: 전문가 2개 제거(r=6)만으로 단일 A100-80G에 배포 가능, ~1.2× 속도 향상, 일반 과제 성능 하락 ≈2.9p(수학 등 도메인 특화는 미세튜닝으로 격차 축소).
- 도메인 특화: 수학 태스크에는 C4 대신 MATH로 보정 데이터를 바꾸면 성능 저하를 크게 줄임(5-shot GSM8K 기준).
방법론(개요)
MoE 층 동작의 핵심 수식
토큰 xx는 라우터 softmax 가중치 상위 kk개의 전문가로 보내지고(예: Mixtral은 k=2k=2), MoE 출력은 선정된 전문가 출력의 가중합:
z=∑j=0k−1w~ej⋅Eej(x)z=\sum_{j=0}^{k-1}\tilde{w}_{e_j} \cdot E_{e_j}(x) (여기서 w~\tilde{w}는 정규화된 라우팅 가중치)
A) Post-Training Expert Pruning (층별, 조합 탐색)
- 작은 보정(calibration) 데이터를 준비(C4 등). 모든 전문가가 켜진 원본 MoE로 추론하면서 각 MoE 층의 입·출력 토큰쌍을 캐시.
- 각 MoE 층에서 보존 전문가 수 r을 정하고, nn명 중 rr명 조합을 열거. 보존 집합 CC에 대해 손실 ∥F′(x,C)−F(x)∥F\|F'(x,C)-F(x)\|_F(출력 재구성 오차의 Frobenius norm)을 계산, 최소 손실 조합만 채택. 그렇게 층별로 이어붙여 최종 pruned MoE 완성.
직관: 채널 프루닝과 유사하게, 원본 출력을 가장 잘 근사하는 전문가 하위집합만 남긴다. (학습·가중치 업데이트 없음)
B) Dynamic Expert Skipping (토큰별 on-the-fly)
- k=2k=2일 때, 라우팅 가중치 we0≥we1w_{e0}\ge w_{e1}. 조건 we1<β⋅we0w_{e1} < \beta \cdot w_{e0} 이면 두 번째 전문가를 스킵. β\beta는 층별로 보정셋에서 w2/w1w_2/w_1의 중앙값으로 설정. 추가 1.2–1.3× 속도 이득 관측.
- 이 기준은 일반 kk에 대해 **오차 상한 HH**로부터 유도 가능. 특히 top-2에선 w2≤HD−H w1w_2 \le \frac{H}{D-H}\,w_1 꼴의 임계로 귀결(여기서 DD는 전문가 출력 간 평균 거리).
실험 결과(요점)
- 일반 과제(LM-Harness 8개 벤치): r=6에서 평균 ≈2.9p 하락, r=4는 ≈7.1p 하락. Wanda(2:4) 대비 성능·메모리·속도 모두 우수(2:4는 특수 하드웨어 의존으로 속도 저하도 관측).
- 프루닝+스킵핑 결합: r=4 + 스킵에서 최대 ~1.33× 속도. r=6+스킵이 r=4 단독과 동급 속도이면서 정확도는 더 높게 유지.
- 도메인 특화(수학): C4로 보정하면 5-shot GSM8K가 크게 떨어지나, MATH로 바꾸면 r=6에서 **51.25%**까지 회복(원본 58.61%). 미세튜닝 후엔 7-expert가 8-expert와 비슷하거나 능가하기도 함.
실전용: Expert Pruning 절차 (Step-by-Step)
- 보정 데이터 수집
- 일반 목적: C4 샘플(예: 128×2048 토큰).
- 도메인 목적: 해당 **도메인 학습셋(MATH 등)**을 동일 형식으로 준비. (보정 셋 크기는 64~128 시퀀스가 안정적)
- 캐싱 추론
- 원본 MoE 모델(모든 전문가 on)로 보정 데이터를 층별로 통과시키며 (입력, 출력) 토큰 텐서를 각 MoE 층마다 캐시.
- 조합 탐색
- 층별 전문가 수 nn과 보존 수 rr을 정하고 (nr)\binom{n}{r} 조합을 열거.
- 각 조합 CC에 대해 Frobenius 재구성 손실 ∥F′(x,C)−F(x)∥F\|F'(x,C)-F(x)\|_F을 계산하여 최소 손실 조합을 선택.
- 모델 구성 & 검증
- 층별로 뽑힌 조합을 이어붙여 pruned MoE 구성(단순 config 변경으로 로딩 가능).
- LM-Harness(ARC, HellaSwag, MMLU 등)로 제로샷 검증 및 토큰/초 측정.
- (선택) 도메인 세팅/미세튜닝
- 도메인 태스크면 보정 셋을 도메인 데이터로 교체하여 재-프루닝.
- 필요 시 소량 파인튜닝으로 성능 격차를 추가 축소/상쇄.
실무 팁
- n=8n=8 수준(Mixtral)에서는 **층별 독립 탐색(layer-wise)**이 **누적 진행(progressive)**보다 **고프루닝률(r=4)**에서 성능 하락이 적었습니다.
실전용: Dynamic Skipping 절차 (Step-by-Step)
- 층별 임계 β\beta 추정
- 보정셋으로 추론하며 각 MoE 층에서 토큰별 w2/w1w_2/w_1 분포를 얻고, 중앙값을 β\beta로 설정.
- 런타임 스킵
- 토큰 xx 처리 시 w2<βw1w_2 < \beta w_1 이면 두 번째 전문가 생략. (일반 kk의 이론적 기준은 부록의 오차 상한식으로 확장 가능)
- 결합 전략
- r=6 + 스킵이 r=4 단독과 동급 속도에 더 높은 정확도를 보여 실전 배포에 유리.
비교 표(실전 재참조용)
구분 내용| 문제 상황 | MoE LLM은 토큰당 소수 전문가만 쓰지만, **전문가 파라미터(≈96%)**가 메모리·배포 병목. Mixtral 8×7B bf16 로딩에 A100-80G×2 필요. |
| 핵심 아이디어 | 학습 없이 전문가 수준 희소화: (A) 층별 조합 탐색 프루닝, (B) 토큰별 동적 스킵핑. |
| 방법(요점) | 프루닝: 보정셋 추론으로 층별 (입·출력) 캐시 → (nr)\binom{n}{r} 조합 중 재구성 손실 최소 조합 유지. 스킵핑: w2<βw1w_2 < \beta w_1이면 2번째 전문가 생략(β\beta=중앙값). |
| 실험 세팅 | LM-Harness 8개 벤치로 제로샷, 속도/피크 메모리 측정. 수학 태스크는 MATH/GSM8K 및 MetaMathQA 미세튜닝 포함. |
| 결과(일반) | r=6: ≈2.9p 하락, ~1.2× 속도. r=4: 더 큰 하락(≈7.1p) vs 더 큰 절감. Wanda(2:4) 대비 성능/메모리/속도 우위. |
| 결과(결합) | r=6+스킵 ≈ r=4 단독 속도(최대 ~1.33×), 정확도는 더 높음. |
| 결과(도메인) | 수학 태스크에서 MATH 기반 보정이 성능 저하를 크게 완화. 미세튜닝 시 7-expert가 8-expert와 동급/상회 가능. |
| 기여 | MoE LLM(디코더) 대상 최초의 사후 전문가 프루닝+스킵핑 프레임워크를 제시, 배포 메모리 절감과 추론 속도 동시 개선. |
| 한계 | (i) 조합 탐색은 전문가 수가 커질수록 비용↑(현행 4~8 전문가에 실용적). (ii) 주 실험 대상은 Mixtral 8×7B로 일반화 추가 검증 필요(논문 논의). (논문 전반 서술에 근거) |
구현·활용 팁
- 탐색 복잡도: 층당 (nr)\binom{n}{r}번 전방패스. Mixtral( n=8n=8 )에서 r=6r=6은 28조합/층이라 실용적(논문에서 r=6 프루닝 시간이 ≈30분, r=4는 ≈90분 보고).
- 프로그레시브 vs 층별 독립: r가 작아지는 고프루닝률에선 층별 독립 방식이 유리.
- 보정셋 크기: 64~128 시퀀스(각 2048 토큰) 권장—1 시퀀스는 불안정.
- 스킵 결합 전략: r=6+스킵은 성능 안전성과 속도의 균형점.
한줄 요약
전문가를 ‘적게, 똑똑하게’ 쓰자: 층별 재구성 손실 최소화 프루닝 + 토큰별 가중치 비율 스킵으로 메모리와 지연을 낮추면서 성능을 최대한 보존한다.
필요하시면, **Hugging Face 기반 코드 스케치(캐시·조합 탐색·β\beta 추정·런타임 스킵)**까지 바로 만들어 드릴게요.
아래 내용은 업로드하신 **“Not All Experts are Equal: Efficient Expert Pruning and Skipping for Mixture-of-Experts LLMs”**를 바탕으로, 방법론을 단계별로 풀어쓴 설명과 직관적 예시, 그리고 **타당성(이론·실증)**과 한계 검증입니다.
방법론 핵심 아이디어 (한 줄)
MoE 층에서 기여도가 낮은 전문가를 사후에 영구 제거하고(Expert Pruning), 추론 시 두 번째 전문가를 조건부로 생략해(Dynamic Skipping) 메모리와 지연을 줄이면서 성능 손실을 최소화한다.
0) MoE 층 동작 복습 (전제)
토큰 xx마다 라우터가 상위 kk개의 전문가를 고르고, 그 정규화 가중치 w~ej\tilde{w}_{e_j}로 전문가 출력의 가중합을 만든다(예: Mixtral은 k=2k=2).
z = ∑j=0k−1w~ej Eej(x)z \;=\; \sum_{j=0}^{k-1}\tilde{w}_{e_j}\,E_{e_j}(x).
문제는 비활성 파라미터(모든 전문가 가중치)가 배포 메모리를 크게 잡아먹는다는 점이다(예: Mixtral 8×7B bf16 로딩에 A100-80G 두 장 필요, 전문가가 전체 파라미터의 ≈96%).
1) Post-training Expert Pruning (학습 없이 전문가 수를 줄이기)
목표: 각 MoE 층에서 nn명의 전문가 중 rr명만 남겨도 원본 출력을 가장 잘 근사하도록, 보존할 전문가 **조합 CC**를 찾는다. 파라미터 업데이트는 없다.
절차 (층별, 두 단계)
- 보정(calibration) 데이터로 원본 MoE(모든 전문가 on)를 통과시키며 각 MoE 층의 (입력, 출력) 토큰쌍 캐시. 일반 모델은 C4 샘플을 사용.
- 층마다 (nr)\binom{n}{r} 조합을 열거하여, 프루닝된 층 F′(x,C)F'(x,C)의 출력이 원본 F(x)F(x)에 가장 가까운 조합(Frobenius 재구성 손실 최소)을 선택:
minC, ∣C∣=r ∥F′(x,C)−F(x)∥F\displaystyle \min_{C,\,|C|=r}\;\lVert F'(x,C)-F(x)\rVert_F. 선택되지 않은 n−rn-r명 전문가는 영구 제거.
효과·구현: 층별로 최적 조합을 뽑아 이어 붙이면 최종 pruned-MoE가 되며, config만 바꿔 로딩 가능. 예컨대 **전문가 2명 제거(r=6)**만으로 Mixtral 8×7B(Instruct)를 A100-80G 단일 GPU에 올릴 수 있었다.
2) Dynamic Expert Skipping (토큰별로 2번째 전문가 생략)
아이디어: 토큰 xx에 대해 상위 두 가중치가 w1≥w2w_1 \ge w_2라면, **w2≤β w1w_2 \le \beta\,w_1**일 때 두 번째 전문가를 생략해도 출력 오차가 상한 HH 이내가 되도록 β\beta를 설정한다(일반 kk에 대한 상한 유도 포함).
β\beta 추정: 보정셋에서 층별로 w2/w1w_2/w_1의 중앙값을 β\beta로 둔다(추론 중 약 절반의 토큰에서 스킵 발생).
속도 이득: 프루닝(r=6, r=4) 위에 스킵핑을 얹으면 **추가 가속(최대 1.33×)**을 얻었다. 특히 r=6+스킵의 속도는 r=4 단독과 동급이면서 정확도는 더 높음.
3) 작동 예시 (Mixtral 8×7B, k=2k=2)
- Pruning: 각 층에서 n=8n=8 전문가 중 r=6r=6만 남기는 조합을 골라 재구성 손실 최소. 이렇게 만든 r=6 모델은 단일 80G에서 구동 가능.
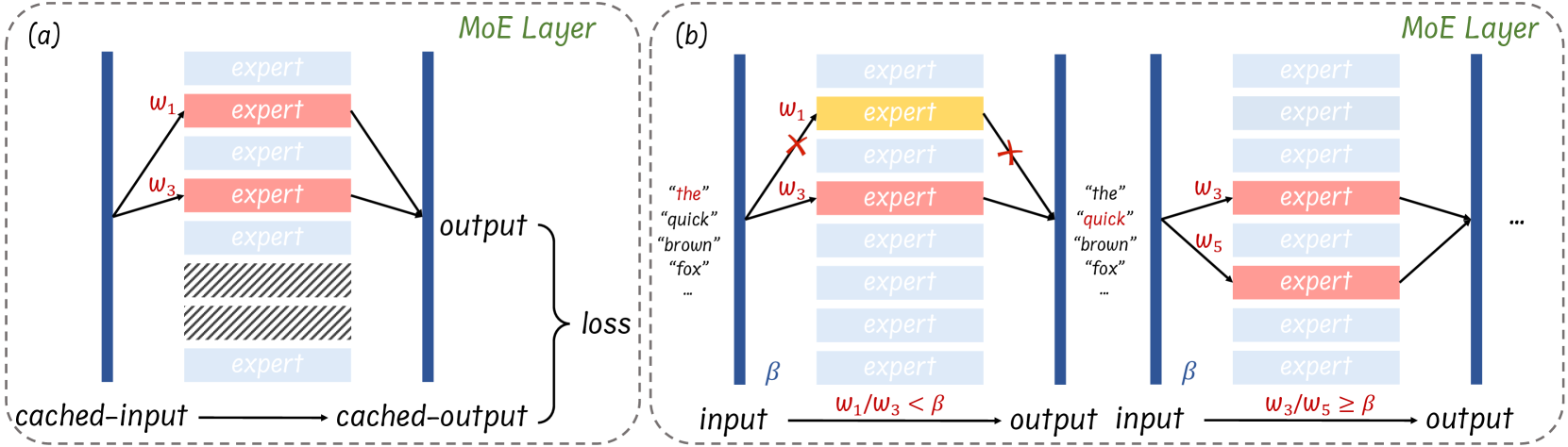
- Skipping: 어떤 토큰에서 w1=0.70, w2=0.20w_1=0.70,\;w_2=0.20, 보정셋으로 추정한 β=0.30\beta=0.30이면 w2/w1=0.286<0.30w_2/w_1=0.286<0.30 이므로 두 번째 전문가 생략. 이 결정을 토큰·층별로 적용한다(그림 3(b) 참고).
4) 성능·자원 지표(요약)
- LM-Harness(8태스크) 평균: r=6 프루닝의 평균 하락 ≈2.9p, r=4는 ≈7.1p.
- 결합 이득: r=6+스킵은 r=4 단독과 **동급 속도(최대 1.33×)**이면서 정확도 ↑.
- 메모리: r=6 → 76%, r=4 → 52% 수준(원본 대비). Wanda 2:4와 비교 시 메모리/성능/속도 면에서 우위(특수 하드웨어 의존도↓).
- 추가 관찰: r=6→4로 줄일 때 가속은 통신 감소 때문이 아니라 캐시 지역성 등 메모리 계층 효과가 주된 원인으로 해석.
5) 도메인 특화 세팅(수학 등)
- C4 보정 → 수학 태스크 성능 급락: r=6에서 GSM8K 58.61→41.02. 보정셋을 MATH로 교체해 완화.
- 미세튜닝: 프루닝 뒤 소량 파인튜닝 시, 7-expert가 8-expert와 동급/상회하기도 함.
- 스킵핑(도메인): 수학 도메인에선 스킵으로 추가 성능 하락이 더 커질 수 있으나, r=6+스킵이 r=4 단독과 같은 속도에 더 높은 정확도를 재현.
6) 방법론의 타당성 (왜 설계가 합리적인가)
이론적 근거
- Pruning은 채널 프루닝과 유사하게 **원본 출력 근사 오차(∥F′(x,C)−F(x)∥F\|F'(x,C)-F(x)\|_F)**를 직접 최소화하므로, 파라미터를 줄여도 층 출력의 보존을 보장하려는 합리적 기준이다.
- Skipping은 출력 차이 L=∥z^−z∥2L=\| \hat{z}-z\|^2에 대해 **상한 HH**를 둬서, 가중치 합 비율로 스킵 가능한 조건을 도출(일반 kk와 top-2의 w2≤βw1w_2 \le \beta w_1 규칙 포함). 오차–가속 트레이드오프가 수식으로 제어된다.
경험적 근거
- LM-Harness 8태스크, GSM8K/MATH 등 광범위 벤치에서 프루닝/스킵 조합이 속도와 성능의 균형을 달성(최대 1.33×, 평균 손실 2.9p@r=6).
- 레이어별(layer-wise) 탐색이 **고프루닝률(r=4)**에서 점진적(progressive) 탐색보다 성능 저하가 적음 → 소보정셋 과적합 방지.
7) 한계와 주의점
- 보정셋 정합성
C4로 프루닝하면 도메인(수학) 성능 급락. 도메인 모델은 MATH 등 동종 분포로 보정해야 한다. - 스킵핑의 도메인 민감도
수학 태스크처럼 어려운 추론에선 스킵으로 인한 성능 손실이 커질 수 있다(그래도 r=6+스킵은 r=4 단독 대비 유리). - 조합 탐색 비용
층당 (nr)\binom{n}{r} 전방패스가 필요(예: n=8n{=}8이면 r=6r{=}6에 28조합). 논문 기준 r=6 ≈30분, r=4 ≈90분(Mixtral 8×7B). - 메모리 감소 한계(스킵)
스킵핑은 런타임 FLOPs 가속이 주효과이고, 가중치 메모리는 줄지 않는다(메모리는 프루닝이 담당). - 하드웨어·스택 의존성
2:4 구조 희소성(Wanda)은 특수 하드웨어 최적화가 없으면 속도 이득이 제한적. 본 방법은 플러그-앤-플레이로 양립 가능(양자화·토큰 프루닝 등과 직교적).
8) 재현용 체크리스트 (실전 절차 요약)
- 보정셋: 일반(C4) 또는 도메인(MATH). 크기는 64–128 시퀀스(각 2048 토큰) 권장.
- 프루닝: 층별로 (nr)\binom{n}{r} 조합을 평가→ 재구성 손실 최소 조합 채택→ config로 전문가 제거 후 로딩.
- 스킵핑: 보정셋에서 층별 β=median(w2/w1)\beta=\mathrm{median}(w_2/w_1) 산출→ 추론 중 **w2≤βw1w_2 \le \beta w_1**면 2번째 전문가 생략.
- 권장 조합: r=6 + 스킵(속도는 r=4와 유사, 정확도는 더 높음).
9) 한눈에 표
항목 요약| 문제 | MoE는 토큰당 일부 전문가만 활성이나, **정적 파라미터(전문가 가중치)**가 배포 병목(예: Mixtral 8×7B는 전문가가 ≈96%, bf16 로딩에 A100-80G×2). |
| 해결 | (A) 층별 Expert Pruning: 재구성 손실 최소 조합 CC만 남김. (B) Dynamic Skipping: w2≤βw1w_2 \le \beta w_1이면 2번째 전문가 생략. |
| 핵심 수식 | (\min_{ |
| 보정셋 | 일반: C4 / 도메인: MATH. 64–128 시퀀스가 안정적. |
| 효과 | r=6에서 평균 ≈2.9p 하락; 프루닝+스킵으로 최대 1.33× 가속. r=6+스킵 ≈ r=4 단독 속도, 정확도↑. |
| 메모리 | r=6: 76%, r=4: 52%(원본 대비). Wanda 2:4 대비 실전 배포 이점. |
| 한계 | 도메인 불일치 시 성능 급락(C4→수학), 스킵은 도메인에서 더 민감, 조합 탐색 비용, 스킵은 가중치 메모리↓ 아님. |
마지막 한 줄 요약
프루닝으로 필요한 전문가만 영구 보존하고, 스킵핑으로 토큰별로 2번째 전문가를 안전하게 건너뛰어 속도·메모리 효율을 크게 끌어올리는 사후 희소화 기법이다.
원하시면, **HF 코드 스니펫(보정셋 캐싱 → 조합 탐색 → β\beta 추정 → 런타임 스킵 적용)**을 바로 만들어 드릴게요.
맞아요. 다만 표현을 조금만 다듬으면 더 정확합니다.
한 줄 정리
- 프루닝: 보정(calibration) 데이터로 각 MoE 층에서 ‘보존할 r개’ 전문가 조합을 고르고, 나머지 n−r개를 영구 제거해 가중치 메모리를 줄입니다.
- 스킵핑: 추론 시 토큰마다 라우팅 가중치가 w2≤β w1w_2 \le \beta\,w_1(층별 임계)면 두 번째 전문가 호출을 생략해 FLOPs/지연시간을 줄입니다.
조금 더 정확히
- Calibration 기반 Expert Pruning
- 층별로 nn명의 전문가 중 **rr**명을 남기는 모든 조합을 평가하고, 원본 층 출력과의 재구성 오차가 가장 작은 조합을 선택합니다.
- 선택되지 않은 n−rn-r 전문가는 모델에서 제거되므로 VRAM·디스크 메모리가 실제로 줄어듭니다.
- “중요하지 않은 전문가 k개를 버린다”라기보다, “보존할 r개를 고르고 나머지를 버린다”가 정확합니다.
- Dynamic Expert Skipping(top-2 기준)
- 각 토큰에서 라우터가 산출한 상위 두 가중치가 w1≥w2w_1 \ge w_2일 때, **w2/w1≤βw_2/w_1 \le \beta**이면 두 번째 전문가를 건너뜁니다.
- β\beta는 층별로 calibration 데이터에서 구한 **w2/w1w_2/w_1의 중앙값(median)**을 씁니다.
- 스킵핑은 가중치 메모리를 줄이지는 않지만, 계산량과 지연시간을 줄입니다.
직관적 예시
- 프루닝(층 L): 전문가 8명 중 조합 평가 결과 **{E1,E3,E4,E5,E7,E8}**이 원본과 가장 비슷 → 이 6개만 남기고 나머지 2개는 삭제.
- 스킵핑(추론 시 토큰 t): w1=0.70, w2=0.20w_1=0.70,\; w_2=0.20, 층 L의 β=0.30\beta=0.30 → 0.20/0.70=0.286<0.300.20/0.70=0.286<0.30 이므로 E2 생략, E1만 실행.
- 반대로 w1=0.52, w2=0.45, β=0.30w_1=0.52,\; w_2=0.45,\; \beta=0.30면 0.45/0.52=0.865>β0.45/0.52=0.865>\beta → 둘 다 실행(난이도 높은 토큰/층에서 정밀도 유지).
타당성(왜 합리적인가)
- 프루닝: “원본 층 출력 근사”를 직접 최소화하므로, 모델 동작을 가장 잘 보존하는 전문가 집합을 남깁니다(학습 없이도 안정적).
- 스킵핑: 출력 오차 상한을 이용해 w2w_2가 충분히 작을 때만 생략하므로, 가속–정확도 트레이드오프를 수식으로 제어할 수 있습니다.
- 실증: r을 중간 수준(예: 6)으로 두고 스킵핑을 결합하면 체감 가속이 발생하면서 정확도 손실은 작게 유지되는 경향이 관찰됩니다.
한계·주의
- 보정셋 정합성: 일반 텍스트(C4)로 프루닝하면 수학 등 특수 도메인 성능이 크게 떨어질 수 있어, 해당 도메인의 **calibration 데이터(MATH 등)**가 필요합니다.
- 스킵핑의 민감도: 추론 난도가 높은 토큰/층에선 w2w_2가 작지 않아 둘 다 실행될 가능성이 커 가속 이득이 줄 수 있습니다.
- 조합 탐색 비용: 층당 (nr)\binom{n}{r} 조합 평가가 필요(예: n=8, r=6 → 28조합/층).
- 효과 분리: 프루닝은 메모리↓, 스킵핑은 FLOPs/지연↓—서로 역할이 다릅니다.
원하시면, 지금 세팅(모델, r 값, β\beta 추정 루틴)을 그대로 돌릴 수 있는 HF 기반 스니펫을 바로 만들어 드릴게요.
https://arxiv.org/abs/2501.00733
On Importance of Layer Pruning for Smaller BERT Models and Low Resource Languages
This study explores the effectiveness of layer pruning for developing more efficient BERT models tailored to specific downstream tasks in low-resource languages. Our primary objective is to evaluate whether pruned BERT models can maintain high performance
arxiv.org

여기서도 layer pruning을 단순하게 진행했습니다.
처음, 중간, 끝을 없애고, 다시 fine-tuning한 후 비교하여 성능을 확인했습니다.
middle이 조금 높게 나온 경우가 많았지만 다들 비등비등했다.
| 문제 상황 | 저자원 언어(마라티어)에서 레이어 프루닝으로 BERT를 작게 만들면서 정확도를 유지할 수 있는지 평가. 대형 모델의 계산/배포 부담을 줄이는 것이 목표. |
| 모델 | 비교 대상: MahaBERT-v2(12L, 모노링구얼), Google-MuRIL(12L, 멀티링구얼), 그리고 스크래치 소형 Marathi BERT-Small(6L), Smaller(2L). 프루닝은 12층 모델들(MahaBERT-v2, MuRIL)에 적용. |
| 데이터 | SHC(헤드라인), LPC(문단), LDC(문서) — L3Cube-IndicNews 계열. 동일 split: Train 22,014, Val 2,750, Test 2,761(총 27,525). 텍스트 길이가 서로 달라 프루닝 효과를 다양한 입력 길이에서 평가. |
| 방법론(프루닝 전략) | Top / Middle / Bottom 위치에서 6개 또는 10개 레이어 제거 후 파인튜닝. Top은 상위 추상 표현층 제거, Middle은 전이 구간, Bottom은 저수준 언어 특징층 제거로 정의. |
| 학습법(파인튜닝·지표) | 프루닝된 각 변형을 SHC/LPC/LDC에 파인튜닝하여 Validation/Testing Accuracy 기록. 모델 크기(레이어/파라미터 감소)도 함께 관찰해 정확도–효율 트레이드오프 분석. |
| 실험 설계 | (a) 프루닝된 12L 모델 변형들 vs (b) 원본 12L vs (c) 동일 깊이의 스크래치 소형 모델을 3자 비교. 세 데이터셋 모두에서 동일한 프로토콜로 평가. |
| 주요 결과(정량) | Testing Acc(%) 요약(Table 2) — MahaBERT-v2: Top-6 92.18/90.80/89.35(SHC/LPC/LDC), Middle-6 90.33/90.55/89.90, Bottom-6 90.47/91.05/90.04. MuRIL: Middle-6 90.69/90.37/88.88, Bottom-6 87.62/89.70/90.11 등. |
| 결과(요지) | (1) 절대적 승자는 없음 — 모델·데이터 조합에 따라 최적 프루닝 위치가 달라짐 (2) Middle 프루닝이 전반적으로 유망 (3) 프루닝+파인튜닝이 동일 크기 스크래치 소형보다 일관되게 우수 (4) 모노링구얼(MahaBERT-v2)가 멀티링구얼(MuRIL)보다 우세 경향. |
| 기여 | (i) 저자원 언어에서 작고(50–80% 깊이 축소)도 성능 경쟁력 유지하는 실증 (ii) Middle 프루닝의 실전적 유효성 (iii) 전략은 조합 의존함을 명확히 제시 (iv) 모노링구얼 > 멀티링구얼 관찰 (v) 프루닝→파인튜닝이 스크래치 사전학습보다 빠르고 실용적. |
| 한계 | (a) 언어 한정(마라티어) — 타 저자원 언어로 일반화 미검증 (b) 태스크 한정(텍스트 분류) — 검색/생성 등 미포함 (c) 시스템 지표(FLOPs/지연/메모리) 정량 보고 제한 (d) 최적 프루닝 위치의 비결정성 → 반드시 전략 스윕 필요. |
| 실무 적용 팁(재현) | ❶ 12층 베이스(모노 vs 멀티)를 선택 → ❷ Top/Middle/Bottom × {6,10}을 생성 → ❸ 각 변형을 과제 데이터로 동일 레시피 파인튜닝 → ❹ 원본/프루닝/스크래치 소형 3자 비교(Val/Test Acc, 레이어 수) → ❺ Middle-k를 기본선으로, 데이터 길이에 따라 Top/Bottom도 검증. |
좋은 자료 업로드 고마워요! 논문 **“On Importance of Layer Pruning for Smaller BERT Models and Low Resource Languages”**를 기반으로, 문제·방법·실험·결과·기여·한계를 한눈에 보이도록 정리하고, 프루닝(레이어 삭제) 절차를 단계별로 설명했습니다. 인용은 논문 원문 라인 범위로 달았습니다.
한 줄 핵심
저자들은 **BERT 계열(특히 마라티어)**에서 레이어 프루닝(Top/Middle/Bottom)을 적용해 작게 만들고도 정확도를 대부분 유지할 수 있음을 보였고, 중간(Middle) 레이어 프루닝이 전반적으로 유망하지만 절대적 승자는 없다고 결론냈습니다. 또한 단일언어(모노링구얼) BERT가 다국어 BERT보다 더 잘했다고 보고합니다.
한 장 요약 표
구분 내용| 문제 상황 | 저자들은 저자원(low-resource) 언어에서 대형 BERT 계열 모델의 계산 비용과 배포 부담을 줄이면서도 분류 정확도를 유지할 수 있는지 탐구. 타깃 언어는 마라티어. |
| 핵심 아이디어 / 방법 | 레이어 프루닝(Top/Middle/Bottom에서 6개 또는 10개 레이어 제거) 후 다운스트림 분류 데이터로 파인튜닝, 원본 12층 모델 대비 작은 모델의 성능 유지 여부 평가. Middle 프루닝이 전반적으로 유망하지만 데이터셋·모델 조합에 따라 최적 전략이 달라짐. |
| 데이터셋 | L3Cube-IndicNews 코퍼스 기반 3종: SHC(헤드라인), LPC(문단), LDC(문서). 각 데이터셋은 동일한 split 크기(Train 22,014 / Val 2,750 / Test 2,761). |
| 모델 | MahaBERT-v2(12L, 단일언어), Google-MuRIL(12L, 다국어), 그리고 MahaBERT-Small(6L), MahaBERT-Smaller(2L)(스크래치 학습) 비교. |
| 실험 설정(프루닝) | Top 6/10, Middle 6/10, Bottom 6/10 제거 후 파인튜닝; 검증/테스트 정확도로 평가. 원본 모델 및 스몰/스몰러와 성능 비교. |
| 주요 결과(요약) | 전반적으로 Middle 프루닝이 경쟁력 있으나 절대적 승자는 없음. 모노링구얼(BERT-v2)이 멀티(MuRIL)보다 우수. 프루닝+파인튜닝은 작은 모델을 처음부터 사전학습하는 것보다 더 빠른 효율 달성. |
| 수치 하이라이트 | 예: MahaBERT-v2 Top-6 → SHC 92.18/LPC 90.80/LDC 89.35, Google-MuRIL Middle-6 → SHC 90.69 / LPC 90.37 / LDC 88.88. 원본 대비 소폭 하락 또는 동급. |
| 기여 | (1) 저자원 언어에서 프루닝→파인튜닝만으로 작고 성능 좋은 과제 특화 모델 제작법 제시 (2) Middle 프루닝의 실증적 유망성 (3) 전략 최적성은 조합 의존 (4) 모노링구얼 > 멀티링구얼. |
| 한계 | (1) 언어가 마라티어로 한정 (2) 분류 태스크 중심(생성/추론 등 미포함) (3) 계산량/추론지연/FLOPs·실시간 메모리 등 시스템 지표 보고 부족 (4) 프루닝 후 세부 하이퍼파라미터·재현성 정보 제한. 저자들도 타 언어 확장 필요성 명시. |
방법론: 프루닝 파이프라인 (Step-by-Step)
- 베이스 선택
- MahaBERT-v2(12층, 단일언어), **Google-MuRIL(12층, 다국어)**을 채택. 비교군으로 Small(6층), Smaller(2층) 스크래치 모델 포함.
- 프루닝 전략 정의
- Top / Middle / Bottom에서 6 또는 10 레이어 제거(=깊이 축소).
- 파인튜닝
- 3개 마라티 분류 데이터셋(SHC/LPC/LDC)으로 과제별 미세조정. 검증/테스트 정확도로 성능 관리.
- 평가 및 비교
- 프루닝된 모델 vs 원본 12층 vs 스크래치 소형 모델(6L/2L) 간 정확도 비교, 크기-성능 트레이드오프 관찰.
실험 결과 해설 (요점 정리)
- 절대적 최적 프루닝 위치는 없음: 데이터셋·모델 조합별로 최적 전략이 바뀜. 다만 Middle 프루닝은 꾸준히 경쟁력을 보임.
- 정량 예시(테스트 Acc, %) — 표 2 요약:
- MahaBERT-v2 Top-6: SHC 92.18, LPC 90.80, LDC 89.35 (SHC에서 최고)
- MahaBERT-v2 Middle-6: SHC 90.33, LPC 90.55, LDC 89.90 (전반적 준수)
- MahaBERT-v2 Bottom-6: SHC 90.47, LPC 91.05, LDC 90.04 (LPC/LDC에서 상위)
- MuRIL Middle-6: SHC 90.69, LPC 90.37, LDC 88.88 (MuRIL 기준 최상 조합)
- 원본 vs 프루닝 모델 vs 스크래치 소형: 프루닝 모델은 동일 크기 스크래치 소형보다 우수하고 원본 대비 소폭 열세/유지 수준을 달성.
- 모노링구얼 우세: 제시된 설정에서 MahaBERT-v2 > MuRIL 경향.
왜 Middle 프루닝이 먹히나? (타당성 해석)
- BERT 내부 표현 흐름을 고려하면, 하위층은 형태/문법, 상위층은 과제 특화 고수준 정보에 치우치는 경향이 있어 중간층에는 일반적·이전이 쉬운 표현이 축적되기 쉽습니다. 중간 일부를 제거하고 재학습하면 중복 표현을 흡수하면서도 상·하위 핵심 기능은 보존될 수 있습니다(논문은 직관적 관찰을 보고; 구체 기제는 추가 연구 필요). 논문도 Middle이 전반적으로 유망하다고만 결론.
한계와 주의점
- 언어/도메인 일반화 미검증: 마라티어로만 평가 → 타 언어(예: 한국어) 확장 검증 필요.
- 시스템 지표 부재: 매개변수/레이어 수 감소 외에 FLOPs, 지연시간(latency), 메모리 등 실사용 지표가 보고되지 않음(후속 실험 권장).
- 태스크 범위 제한: 분류 중심. 임베딩/검색·생성 등 다른 태스크로의 전이 분석 부족. (저자들은 관련 맥락으로 SBERT 프루닝이 주로 임베딩에 초점을 맞췄음을 언급)
실무 적용 가이드(한국어/다국어 세팅에 이식 시)
- 베이스 선택: 한국어 단일언어 BERT(예: KR-BERT), 혹은 다국어 베이스(mBERT, XLM-R).
- 프루닝 후보 구성: Top/Middle/Bottom 각각에서 k% 깊이 축소(예: 50% 또는 80%) 안배. 이 논문은 6/10층 제거를 대표값으로 사용.
- 파인튜닝: 당신의 과제 데이터(분류/특정 도메인)에 맞춰 프루닝 후 파인튜닝.
- 평가: 원본/프루닝/동일 크기 스크래치 모델 3자 비교(정확도+실사용 지표). 논문은 정확도로만 평가했으니, 추가로 추론 속도·GPU 메모리·에너지를 병행 기록 추천.
- 전략 선택: 먼저 Middle 프루닝을 베이스라인으로 삼고, 데이터셋 성격(짧은 문장 vs 긴 문서)에 따라 Top/Bottom도 실험하여 조합별 최적을 찾기. 절대적 승자 없음에 유의.
메모(연구 맥락 연결)
- 논문은 레이어 드롭/프루닝이 트랜스포머에서도 현실적 대안임을 재확인하며, 사전학습을 새로 하지 않고도 과제 맞춤 소형화를 시연합니다. SBERT 프루닝이 임베딩 중심이었던 데 비해, 본 연구는 텍스트 분류에 초점을 맞춘 점이 차별점입니다.
원문 기반 요약은 여기까지고, 필요하시면 당신의 한국어 분류/검색/생성 파이프라인에 바로 이식할 실험 체크리스트(코드 스니펫·레이어 인덱스 매핑·학습/평가 스크립트 구조)도 만들어 드릴게요.
좋아요. 업로드하신 **“On Importance of Layer Pruning for Smaller BERT Models and Low Resource Languages”**를 딱 방법론 관점에서, 이해가 잘 되도록 예시까지 곁들여 체계적으로 정리해 드립니다. 핵심 인용은 논문 원문 라인으로 달았습니다.
무엇을 했나? (문제 설정 → 방법론 개요)
- 문제: 저자원 언어(마라티어)의 분류 과제에서, BERT를 **레이어 프루닝(깊이 축소)**으로 작게 만들면서 정확도를 최대 보존할 수 있는가?【turn2file5†L8-L16】
- 아이디어: 12층 BERT(MahaBERT-v2, Google-MuRIL)에 대해 Top/Middle/Bottom 위치에서 6개 또는 10개 레이어를 제거하고, 프루닝 후 파인튜닝으로 성능을 회복·평가한다. 비교군으로 **6층/2층 소형 모델(스크래치 학습)**도 둔다.【turn2file0†L21-L29】【turn2file0†L31-L49】【turn2file3†L14-L23】【turn2file3†L27-L40】
- 데이터: L3Cube-IndicNews 기반 SHC(헤드라인), LPC(문단), LDC(문서) 세 과제. 모든 데이터셋의 split 크기는 동일(Train 22,014 / Val 2,750 / Test 2,761).【turn2file0†L7-L11】【turn2file0†L51-L63】【turn2file4†L19-L24】
방법론을 단계별로 (Step-by-Step)
1) 베이스 모델·데이터 확정
- 모델: MahaBERT-v2(12L, 단일언어), Google-MuRIL(12L, 다국어), 비교용 MahaBERT-Small(6L), MahaBERT-Smaller(2L)【turn2file0†L21-L49】【turn2file4†L1-L11】
- 데이터: SHC/LPC/LDC 세 과제에 대해 동일 split로 학습·평가【turn2file0†L51-L63】【turn2file4†L26-L48】
2) 프루닝 전략 정의(Top/Middle/Bottom, k∈{6,10})
- Top-k: 상위 레이어 k개 제거(포괄적 의미 표현층)【turn2file3†L19-L25】
- Middle-k: 중간 레이어 k개 제거(하위–상위 표현의 전이 구간)【turn2file3†L27-L33】
- Bottom-k: 하위 레이어 k개 제거(형태/문법·로컬 특징층)【turn2file3†L34-L40】
- 모든 경우 k=6 또는 10으로 실험【turn2file0†L27-L37】
🔎 작동 예시(직관용): 12층 BERT에서 Top-6는 7–12층 제거, Bottom-6는 1–6층 제거, Middle-6는 가운데 6층(예: 4–9층) 제거 후 남은 레이어를 직렬로 이어서 사용. 그 다음 파인튜닝으로 적응.
3) 프루닝 후 파인튜닝
- 각 프루닝 변형(Top/Middle/Bottom × {6,10})을 각 과제 데이터로 파인튜닝하고, 검증·테스트 정확도를 기록한다.【turn2file0†L10-L14】【turn2file3†L42-L50】
4) 평가·비교 지표
- Testing/Validation Accuracy 중심으로 성능 확인, **모델 크기(레이어 수 감소)**를 같이 관찰해 정확도–효율 트레이드오프를 본다.【turn2file3†L42-L53】【turn2file3†L55-L57】
- 비교 그룹: (a) 프루닝된 모델 vs (b) 원본 12층 vs (c) 동일 크기 스크래치 소형 모델【turn2file0†L12-L14】【turn2file3†L11-L12】
결과가 시사하는 방법론의 타당성(왜 이게 먹히는가?)
- Middle 프루닝의 일관된 경쟁력
- “전반적으로 중간 프루닝이 유망하지만 절대적 승자는 없다”는 결론을 반복적으로 확인.【turn2file3†L68-L73】【turn2file10†L1-L5】
- 수치 예시(Table 2, 테스트 Acc, %):
- MahaBERT-v2 / SHC: Top-6 92.18 > Middle-6 90.33, Bottom-6 90.47【turn2file6†L9-L13】【turn2file7†L23-L33】
- MuRIL / SHC: Middle-6 90.69 (Top-6 89.08, Bottom-6 87.62)【turn2file6†L16-L18】【turn2file7†L30-L35】
- LPC/LDC에서도 조합별 차이는 있으나 Middle-6이 자주 상위권.【turn2file6†L41-L49】【turn2file11†L19-L27】
- 프루닝+파인튜닝의 우위(동일 크기 스크래치 대비)
- 프루닝 모델이 동일 크기 스크래치 모델보다 일관되게 좋음, 풀 모델과도 근접.【turn2file12†L1-L9】
- 예) Table 2: MahaBERT-Small/Smaller보다 프루닝된 변형들이 종종 상위 정확도.【turn2file6†L23-L27】
- 모노링구얼 > 멀티링구얼(이 세팅에서는)
- 같은 프루닝 세팅에서 **MahaBERT-v2(단일언어)**가 **MuRIL(다국어)**보다 전반적으로 우세하다는 관찰.【turn2file1†L79-L84】【turn2file8†L19-L21】
이유(해석): 하위층은 로우레벨, 상위층은 과제특화 표현을 맡는 경향이 있어 중간 일부를 걷어내도 상/하위 핵심 기능이 남고, 파인튜닝으로 중복 표현을 재조정하며 회복된다는 직관과 부합. 논문도 “중간 프루닝이 균형적”이라 결론.【turn2file10†L1-L5】
한계(방법론의 적용 시 주의)
- 언어 범위 제한: 평가가 마라티어에 한정 → 한국어/다른 저자원 언어 일반화는 후속 검증 필요.【turn2file10†L34-L37】
- 태스크 범위: 텍스트 분류 중심. 생성·검색 등은 미포함. (지표도 정확도 중심, 시스템 지표는 주로 레이어 수 관찰)【turn2file3†L42-L53】
- 전략의 비결정성: 절대적 최적 프루닝은 없음. 데이터/모델 조합별로 달라, 반드시 여러 전략을 스윕해야 함.【turn2file10†L1-L5】
“내 프로젝트에 적용해보자” 실전 가이드(논문 기반 프로세스)
- 베이스 선택: 목표 언어·도메인에 맞는 12층 BERT(예: 한국어 KR-BERT or mBERT).
- 프루닝 후보 구성: **Top/Middle/Bottom × k∈{6,10}**를 일괄 생성(깊이 50%·80% 축소 시나리오)【turn2file0†L27-L37】【turn2file3†L19-L40】
- 프루닝 후 파인튜닝: 과제 데이터로 동일한 하이퍼 파라미터 세팅으로 미세조정, Val/Test Acc 수집【turn2file0†L10-L14】【turn2file3†L42-L50】
- 3자 비교: 원본 vs 프루닝 vs 동일-깊이 스크래치 성능을 표로 비교. (논문에서는 프루닝이 스크래치 소형보다 우수)【turn2file12†L1-L9】
- 최종 선택: Middle-k부터 시작하되, 데이터 길이·도메인 따라 Top/Bottom도 확인(논문 결론)【turn2file10†L1-L5】
한눈에 보는 수치 하이라이트(방법론 타당성 근거)
- Table 2 (Testing Acc, %):
- MahaBERT-v2: SHC Top-6 92.18, LPC Top-10 92.00, LDC Bottom-6 90.04【turn2file6†L9-L16】【turn2file11†L19-L24】
- MuRIL: SHC Middle-6 90.69, LPC Middle-6 90.37, LDC Bottom-6 90.11【turn2file6†L16-L22】【turn2file11†L24-L27】
- 요약: 조합별 최적이 다르되, Middle 프루닝이 안전한 출발점. 스크래치 소형보다 프루닝+파인튜닝이 일관 우세【turn2file10†L1-L5】【turn2file12†L1-L9】.
마지막 정리(한 줄)
절차는 단순: 12층 BERT → Top/Middle/Bottom 중 하나로 6/10층 제거 → 해당 과제로 파인튜닝 → 원본·스크래치 소형과 3자 비교. Middle 프루닝이 대체로 유망하지만 최적 전략은 조합 의존이다.【turn2file3†L14-L23】【turn2file3†L27-L40】【turn2file10†L1-L5】
필요하시면, 이 방법론을 **한국어 분류·검색(예: MTEB-KR 하위 태스크)**에 바로 붙일 수 있게 **실험 스크립트 골격(레이어 인덱스 지정, 프루닝 후 로더/헤드 재연결, 학습 루프, 결과 표 자동화)**까지 만들어 드릴게요.
요약 결론은 거의 맞아요. 다만 “왜/어떻게 비교했는지”와 “관찰된 패턴”을 한두 줄 더 넣으면, 나중에 보더라도 바로 실험을 복원할 수 있어요. 아래처럼 정리해두면 탄탄합니다.
추천 3문장 요약
- 저자원 언어(마라티어) 분류 과제에서 12층 BERT(MahaBERT-v2, MuRIL)에 **Top/Middle/Bottom 레이어 프루닝(6/10층 제거)**을 적용한 뒤 각 과제로 파인튜닝하여 성능을 비교했다.
- Middle 프루닝이 자주 상위였지만 데이터셋·모델 조합에 따라 최적 위치는 달라 절대적 승자는 없었다.
- 프루닝+파인튜닝 모델이 동일 깊이의 스크래치 소형 모델보다 대체로 우수했고, 같은 조건에서 모노링구얼(MahaBERT-v2)이 멀티링구얼(MuRIL)보다 우세한 경향을 보였다.
초간단 버전(2줄)
- 처음/중간/끝 레이어를 각각 잘라내고(f=6,10), 프루닝 후 파인튜닝 → 정확도 비교
- Middle가 약간 우세한 경우가 많았지만 비등비등, 프루닝+FT > 스크래치 소형, 모노 > 멀티 경향
재현 메모(데이터·학습법 한 줄)
- 데이터: SHC(헤드라인)·LPC(문단)·LDC(문서) 동일 split
- 학습법/지표: 프루닝 변형별 동일 레시피로 파인튜닝, Val/Test Accuracy로 비교, 원본(12L)·프루닝(12→kL)·스크래치(6L/2L) 3자 비교
원하시면 위 3문장 요약을 논문 표/포스터용 1-슬라이드 템플릿이나 실험 체크리스트(레이어 인덱스 프리셋, 결과 자동 집계 스크립트)로 바로 변환해드릴게요.
'인공지능 > 논문 리뷰 or 진행' 카테고리의 다른 글
| LLM의 중간 계층 표현 능력 논문 리뷰 - LLM middle layer representation ability (0) | 2025.09.05 |
|---|---|
| Language Model 파라미터 감소(Pruning) 논문 5 (1) | 2025.09.03 |
| Language Model 파라미터 감소(Pruning) 논문 3 (6) | 2025.09.02 |
| Language Model 파라미터 감소(Pruning) 논문 2 (0) | 2025.09.02 |
| ULLME: A Unified Framework for Large Language Model Embeddings with Generation-Augmented Learning (4) | 2025.08.27 |