https://arxiv.org/abs/1910.09457
Aleatoric and Epistemic Uncertainty in Machine Learning: An Introduction to Concepts and Methods
The notion of uncertainty is of major importance in machine learning and constitutes a key element of machine learning methodology. In line with the statistical tradition, uncertainty has long been perceived as almost synonymous with standard probability a
arxiv.org
2020년 논문으로 좀 오래된 논문입니다.

예시부터가 ImageNet으로 오래된 것을 잘 보여줍니다 ㅎㅎ
머신러닝에서 Aleatoric(우연적) Uncertainty와 Epistemic(지식적) Uncertainty를 구분하고, 그 처리 방법을 소개했습니다.
| 불확실성 유형 | 정의 | 예시 | 특징 |
| Aleatoric uncertainty | 데이터의 내재적 랜덤성으로 인한 불확실성 | 동전 던지기의 앞/뒤 확률 | 불가피성, 추가 정보로 감소 불가능 |
| Epistemic uncertainty | 모델이나 지식의 부족으로 인해 발생하는 불확실성 | 모르는 언어의 단어의 뜻 추측 | 가변성, 추가 데이터로 감소 가능 |
AU는 줄일 수 없고, EU는 줄일 수 있기에 Version Space Learning, Bayesian Inference를 통해 줄이려고 노력했습니다.
지금 NLP론 하긴 어려운 방법 같아 더이상 깊게 들어가진 않겠지만 그래도 AU, EU를 수학적으로 구분하고 개념적으로 정리했다는 것에선 큰 기여를 보였습니다.
| 🔍 연구 목적 | 머신러닝의 예측 불확실성을 두 가지(Aleatoric & Epistemic)로 구분하고, 이를 정량화·모델링하는 이론적 프레임워크 제시 |
| 🧠 핵심 개념 | • Aleatoric uncertainty: 데이터 자체의 내재적 랜덤성 (줄일 수 없음) • Epistemic uncertainty: 모델 또는 지식 부족에서 기인 (데이터/지식으로 줄일 수 있음) |
| 📐 불확실성 분해 구성 | 전체 예측 오류 = Aleatoric + Epistemic Epistemic = Model Uncertainty + Approximation Error |
| 🛠 주요 방법론 | ① Version Space Learning: 가능한 모든 가설을 유지하며 예측을 다수결/집계하여 불확실성 표현 ② Bayesian Inference: 가설 공간에 확률분포를 부여해 사후 분포를 기반으로 예측 및 불확실성 추정 |
| ✅ 활용 분야 | • Active Learning (정보 부족 구간 우선 학습) • Out-of-Distribution 탐지 • 예측 신뢰도 시각화 • 안전성 요구가 높은 시스템 (예: 의료, 자율주행) |
| ⚠ 한계점 | • 실험 기반 결과 부족 (정성적 설명 중심) • 딥러닝에 대한 직접적 연결은 약함 • Bayesian/Version Space의 계산 복잡도 큼 • Aleatoric의 정량화 방법은 간단히만 언급됨 |
| 🏆 기여 요약 | • 머신러닝 예측 불확실성을 체계적으로 구분 및 모델링 • 개념적/수학적 정리를 통해 다양한 기법을 비교할 수 있는 기준 제시 • 후속 연구(uncertainty-aware training, model calibration 등)의 이론적 기초 제공 |
https://arxiv.org/abs/2409.03021
CLUE: Concept-Level Uncertainty Estimation for Large Language Models
Large Language Models (LLMs) have demonstrated remarkable proficiency in various natural language generation (NLG) tasks. Previous studies suggest that LLMs' generation process involves uncertainty. However, existing approaches to uncertainty estimation ma
arxiv.org

이 논문은 시퀸스를 Concept 단위로 분해하여 각각의 Uncertainty를 측정합니다.
Output을 통해 Concept를 샘플링하네요 ㅎㅎ....
샘플링 한 것을 Classifier모델 태워서 점수 내는 방식으로 음.... 저희가 쓰기엔 애매한 방법입니다.

AU, EU 구분도 딱히 없어서 그렇구나 하는 정도로 넘어가겠네요 ㅎㅎ.,.
| 연구 배경 | 기존 LLM 불확실성 추정은 대부분 시퀀스 단위로만 수행되어, 문장 내 여러 정보 단위(예: 사실, 주장 등)를 분리해 평가하지 못함 (정보 얽힘 문제: Information Entanglement) |
| 문제의식 | - 하나의 문장에 포함된 정보들이 각각 다르게 신뢰될 수 있음에도 불구하고 - 기존 방식은 전체 문장을 통째로 “불확실하다/확실하다”로만 판단함 → 어떤 정보가 hallucination인지를 pinpoint 불가 |
| 핵심 아이디어 | 문장을 의미 단위인 “concept”로 분해하고, 각 개념에 대해 개별적으로 불확실성을 추정함 |
| 전체 구조 (CLUE 프레임워크) | ① LLM을 활용해 출력 문장에서 개념 추출 ② 유사 개념 통합 (NLI 기반 entailment 양방향 평가) ③ Output 문장과 각 개념의 entailment score 계산 ④ score들의 -log 평균 → 개념별 uncertainty 추정 |
| Entailment Score 계산법 | - 사용 모델: bart-large-mnli - 문장과 개념 간 entailment 여부를 softmax로 확률화 - 문장 = premise, 개념 = hypothesis ("This example is about {concept}") |
| 불확실성 계산식 |  ⇒ 개념 c_j가 여러 샘플 o_i에서 얼마나 일관되게 포함되는지 평가 |
| 실험 설정 | - 모델: GPT-3.5-turbo-instruct (N=5 샘플링) - 불확실성 계산에만 output 사용 (black-box 가능) - 데이터셋: ELI5-Category / WikiQA / QNLI |
| 실험 1: Hallucination 탐지 | - 개념 불확실성과 정답 entailment score 간 음의 상관관계 확인 - CLUE가 baseline(NLI classifier) 대비 AUROC +21%p 개선 |
| 실험 2: 인간 평가 정합성 | - MTurk 실험 결과: CLUE가 기존 방식 대비 +33% 정확도 향상 (91% vs 58%) ⇒ 개념 단위 불확실성이 사람의 판단과 더 잘 맞음 |
| 실험 3: 다양성 측정 지표로 활용 | - 개념들을 상·하위 구조로 정의 (ex: tone → happy/sad/serious) - 개별 개념 불확실성을 기반으로 entropy, harmonic mean으로 다양성 정량화 |
| 장점 및 기여 | ✅ 정보 얽힘 문제 해결 → 개별 정보 단위 평가 가능 ✅ black-box 모델 적용 가능 ✅ 해석 가능성, 설명력 우수 ✅ Hallucination 탐지, 다양성 측정 등 다양한 활용 가능성 |
| 한계점 | ⚠️ 개념 추출 및 score 계산이 사용하는 LLM 품질에 민감 ⚠️ NLI classifier의 편향이 전체 시스템에 영향 가능 ⚠️ 고차 개념 다양성 평가 benchmark 부재 |
| 결론 | CLUE는 시퀀스를 의미 단위로 분해하고, 개념마다 불확실성을 정량화하는 최초의 프레임워크로서, 해석 가능한 LLM 평가 방법으로 학문적·실용적 기여도가 높음 |
https://arxiv.org/abs/2311.01740
SAC3: Reliable Hallucination Detection in Black-Box Language Models via Semantic-aware Cross-check Consistency
Hallucination detection is a critical step toward understanding the trustworthiness of modern language models (LMs). To achieve this goal, we re-examine existing detection approaches based on the self-consistency of LMs and uncover two types of hallucinati
arxiv.org
이 논문은 Black-box 환경에서 Hallucination 탐지를 진행합니다.
기존 Self-consistency방식은 질문에 오류가 있거나, 모델에 오류가 있으면 탐지하지 못하기에 새로운 프레임 워크를 통해 측정합니다.

저희가 간과하는 두가지 상황을 보여주고 있습니다.

일관성이 있더라도 사실은 아닐 수 있으니.....

질문을 새로 만들고(의미는 같지만 표현은 다르게) target lm과 verifier lm을 통해 출력을 만들어 의미가 같은 출력을 만드는지 확인하는 과정을 통해 판단한다.
📐 세부 Score 계산 방식
1. Self-check Score (SC2)
- 동일 질문 Q₀에 대한 여러 샘플 답변들과 의미 일치 여부 평가
- score 낮음 = high consistency (→ 사실일 가능성)
2. Question-level Consistency (SAC3-Q)
- Q₁~Qₖ에 대해 얻은 답변들과 Q₀-답변의 의미 일치도 평가
- 다양한 표현의 질문에서 동일한 잘못된 답을 주면 hallucination 가능성↑
3. Model-level Consistency (SAC3-M, SAC3-QM)
- 같은 질문을 verifier LM에 주고 응답 비교
- 또, Q₁~Qₖ도 verifier LM에 주고 cross-check
- 타 모델은 “예”인데 GPT만 “아니요”면 → GPT가 hallucinate 중일 수 있음
4. 최종 Score:
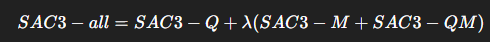
- λ는 verifier LM 신뢰도 (기본 1.0, 전문가 도메인 모델일 경우 가중치↑)
| 📌 논문 목적 | Self-consistency 기반 hallucination 탐지의 한계를 보완하고, Black-box LLM 환경에서도 신뢰도 있는 hallucination 탐지 기법 개발 |
| ❗ 문제의식 | - LLM은 질문에 대해 일관되게 틀린 답을 낼 수 있음 (self-consistency만으로는 탐지 실패) - 다른 모델과 의견이 다르면 모델 자체의 오류일 수 있음 (model-level hallucination) |
| 🔧 제안 기법 (SAC3) | ✅ 질문 재구성 (Semantic Perturbation) ✅ 다른 모델과 응답 비교 (Cross-model Check) ✅ QA 쌍 전체의 의미 일치 평가 → Self-check + Cross-Q (SAC3-Q) + Cross-M (SAC3-M/QM) 점수 통합 |
| 📐 핵심 구성 요소 | ① Self-checking (SC2): 동일 질문 다중 샘플 ② SAC3-Q: 의미 동일한 질문 여러 개 생성 후 응답 비교 ③ SAC3-M, QM: 다른 LM (verifier)와 응답 비교 |
| 🧠 주요 인사이트 | - 일관된 오류도 hallucination이다 → self-consistency는 충분조건 아님 - 질문을 바꿔도 계속 틀리는 건 질문 레벨 hallucination - 다른 LLM과의 차이는 모델 레벨 hallucination의 지표가 됨 |
| 📊 성능 요약 | - Classification QA에서 기존 방식 대비 +30~50% 이상 AUROC 향상 - Generation QA에서도 AUROC 기준 +7~13% 향상 - GPT-3.5, GPT-4, PaLM 등 다양한 모델에 적용 가능 |
| ⚖️ 장점 | - External knowledge 없이 동작 - 완전 black-box 모델 (ChatGPT 등)에도 적용 가능 - 모델-질문 다양성 고려한 정교한 탐지 구조 |
| ⚠️ 한계 | - QA 중심 실험에 국한 - 의미 비교도 결국 LLM 기반으로 오류 가능성 존재 - 계산량 증가 (sampling + QA pair 비교 필요) |
| 🏅 기여점 | ✅ Black-box LLM에 적합한 hallucination 탐지 구조 ✅ 질문 다양성과 모델 다양성 모두 활용 ✅ QA pair 일관성에 집중한 정밀 탐지 기법 제안 ✅ 다양한 모델·태스크에서 SOTA 수준 성능 입증 |
https://arxiv.org/abs/2311.08718?utm_source=chatgpt.com
Decomposing Uncertainty for Large Language Models through Input Clarification Ensembling
Uncertainty decomposition refers to the task of decomposing the total uncertainty of a predictive model into aleatoric (data) uncertainty, resulting from inherent randomness in the data-generating process, and epistemic (model) uncertainty, resulting from
arxiv.org
이 논문은 AU와 EU를 명확하게 나누고, 정확하게 이해하려고 하였습니다.

입력을 명확하게 만들어서 출력을 확인합니다.
입력을 명확하게 만드는 것 자체가 모호한 질문에 정보를 추가하는 것으로 답변은 다양해질 수 밖에 없습니다.
답변을 모아 답변 다양함을 통해서 AU를 측정하고, 모델의 평균적인 확신도를 통해 EU를 측정했습니다.
근데 저는 납득하질 못하겠어서...
이게 왜 되는지,...

📦 직관적 예시
🔸 입력:
"Who is the president of this country?"
🔸 Clarification LLM 생성:
- “Assume ‘this country’ refers to the United States in 2024.”
- “Assume the question is about France in 2020.”
- “Assume this refers to Brazil in 2018.”
🔸 각 clarified input에 대한 예측:
- C₁: "Joe Biden"
- C₂: "Emmanuel Macron"
- C₃: "Jair Bolsonaro"
→ 답이 서로 다르기 때문에 Aleatoric Uncertainty ↑ (입력 자체의 모호함으로 인한 다양성)
🔸 각 예측의 확률분포 엔트로피 (Epistemic 측정):
- C₁: 90% 확신 (Low entropy)
- C₂: 85% 확신
- C₃: 88% 확신
→ 각 clarification에서는 모델이 잘 예측 (즉, Epistemic Uncertainty ↓)
| 📌 논문 목적 | LLM의 예측 결과에 대한*총 불확실성(total uncertainty)을, ① 입력의 모호성에서 오는 Aleatoric uncertainty와 ② 모델의 지식 부족에서 오는 Epistemic uncertainty로 분해 |
| 🧠 핵심 아이디어 (ICE) | 입력을 다양한 clarification (명확화 문장)으로 바꾸어 LLM 예측을 수행 → 예측 간 다양성으로 AU 측정, 각 예측의 확신도로 EU 측정 |
| 📊 주요 실험 결과 | - Mistake detection (NQ/GSM8K): AUROC 최대 89.7 - Ambiguity detection (AmbigQA): AUROC 최대 71.7 - Clarification 후 AU 감소 및 정답 recall 향상 |
| 🧩 이점 및 인사이트 | ✅ 파라미터 수정 없이 black-box LLM에 적용 가능 ✅ AU 분해로 모호한 질문 탐지 및 사용자 피드백 가능 ✅ 기존 Deep Ensemble / BNN 방식의 구조적 대안 |
| ⚠️ 한계점 | - Epistemic 정의는 proxy적이며 정확한 베이지안 의미와는 차이 있음 - Clarification LLM 품질에 의존 - K개의 clarification으로 인해 계산 비용 증가 |
| 🏅 기여 요약 | ✔ 새로운 불확실성 분해 방식 제안 ✔ 실용적 black-box 적용 가능성 확보 ✔ 입력 다양성 기반 AU 추론이라는 새로운 관점 제시 ✔ AmbigInst 등 새로운 평가 데이터도 제작 |
'인공지능 > 논문 리뷰 or 진행' 카테고리의 다른 글
| Uncertainty estimation 관련 논문 정리 - 3 (1) | 2025.05.16 |
|---|---|
| Uncertainty estimation 관련 논문 정리 - 2 (1) | 2025.05.15 |
| L2M - Least-to-Most Prompting Enables Complex Reasoning in Large Language Models (2) | 2025.05.13 |
| Decomposed Prompting: A Modular Approach for Solving Complex Tasks (0) | 2025.05.12 |
| To Believe or Not to Believe Your LLM (0) | 2025.05.11 |