https://arxiv.org/abs/2406.02543
To Believe or Not to Believe Your LLM
We explore uncertainty quantification in large language models (LLMs), with the goal to identify when uncertainty in responses given a query is large. We simultaneously consider both epistemic and aleatoric uncertainties, where the former comes from the la
arxiv.org
AU - 대답의 모호성
EU - 학습의 부족 !
이 논문도 결국 샘플링이라 해야 하나, 반복적인 모델 출력을 통해 uncertainty를 추정하네요
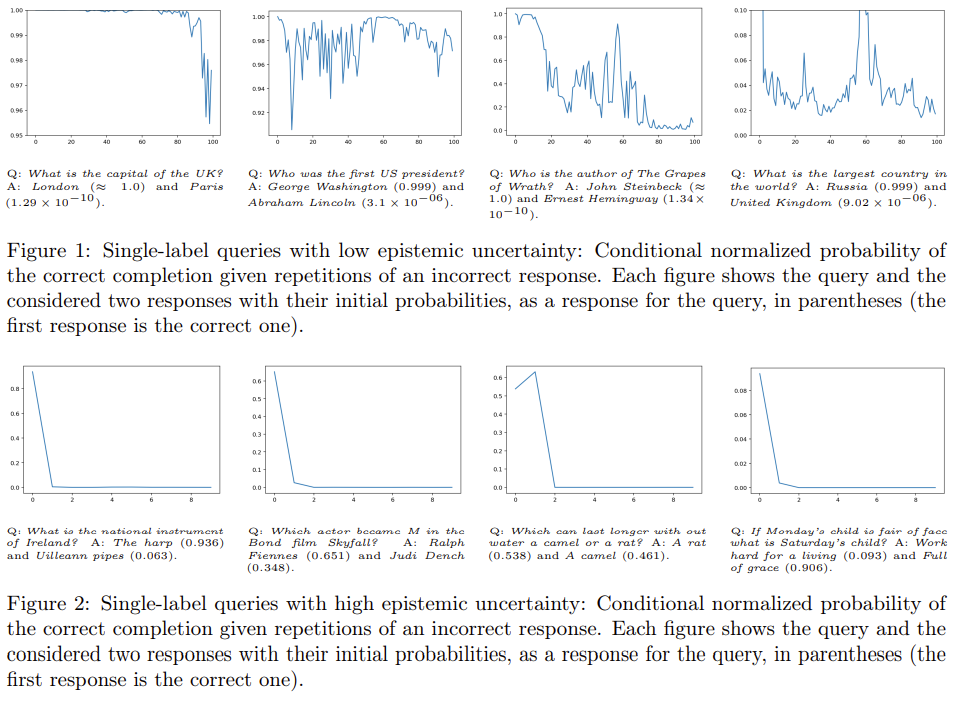
확신이 강한 경우엔 오답을 제시해도 흔들리지 않지만(Figure 1) 확신이 약하면 오답을 제시하면 오답이 확률이 오르고, 정답은 점점 0에 수렴한다.
| 조건 | 결과 | 의미 |
| 질문 X가 자주 학습된 경우 | 정답 유지, Softmax가 X에 집중 | In-weight 학습 성공 → EpU 낮음 |
| 질문 X가 드문 경우 + 오답 Y 반복 | Y가 Softmax를 지배 → 오답 출력 | In-context 학습에 의해 흔들림 → EpU 높음 |
| Y가 많이 반복될수록 | Softmax에서 Y의 비중 증가 | 확률 증폭 효과 (hallucination 가능) |

| 분포 | 설명 |
| 초록색 곡선 P~ | 실제 정답이 존재하는 위치의 분포 → ground truth에서 가능한 응답들이 집중된 구간 |
| 빨간색 곡선 Q~ | LLM이 반복 프롬프트를 통해 생성한 응답 분포 |
| 해석 | Q~가 높은 확률을 부여한 구간이 실제 P~에선 거의 0에 가까움 → hallucination 발생 → 모델은 “자신만의 답”을 확신하며 생성했지만, 실제론 말이 안 되는 구간 |
그런데 정답 P는 알 수 없으니 하한추정을 진행합니다.

| 상황 | MI | Epistemic Uncertainty | 해석 |
| 응답들이 서로 독립적 | ≈ 0 | 낮음 | 모델이 확신 있음 |
| 응답들이 서로 영향받음 | ↑ | 높음 | 모델이 불확실 / 흔들림 |
| 응답 분포 Q~가 정답 분포 P~와 다름 | ↑ | 높음 | hallucination 가능성↑ |

| M.I. ≈ S.E. (low entropy 단일 정답) | TriviaQA, AmbigQA 단독 실험 (LLM 확신 있음) |
| M.I. > S.E. (high entropy 다중 정답) | WordNet 포함 실험 (모델 불확실성 존재) |
| WordNet 데이터셋의 효과 | S.E.는 threshold tuning에 민감해 precision ↓ M.I.는 종속성 기반으로 robustness ↑ |
| 실험 시사점 | multi-label 환경에서야 M.I.의 진가가 드러남 |
| 연구 배경 및 문제의식 | - LLM은 종종 hallucination (지식 왜곡)을 발생 - 기존 UQ(Uncertainty Quantification)는 logprob/entropy 기반으로 aleatoric과 epistemic을 구분하지 못함 - 다중 정답 상황(multi-answer)에선 기존 방식이 혼동을 야기함 |
| 목표 | - Epistemic uncertainty만을 정확히 측정하여 신뢰할 수 없는 응답(hallucination)을 탐지 - 다중 정답(aleatoric uncertainty 포함) 환경에서도 적용 가능해야 함 |
| 핵심 아이디어 | - 동일한 질문에 대해 반복적으로 응답을 생성 - 이전 응답들을 prompt에 포함하여 모델이 얼마나 영향을 받는지 측정 - 응답 간 의존성이 높으면 → epistemic uncertainty가 높음 |
| 방법론 요약 | 🔹 Iterative Prompting: Y₁ ← Q(x), Y₂ ← Q(x + Y₁), … 반복적으로 생성 🔹 Pseudo Joint Distribution Q~ 생성 🔹 Mutual Information I(Q~): 응답 간 의존도 측정 → Epistemic UQ의 하한선 🔹 Hallucination Score = MI가 클수록 hallucination 가능성 ↑ |
| 예시 | - Q: What is the capital of the UK? → "London"은 반복된 “Paris”에도 흔들리지 않음 → EpU 낮음 - Q: What is the national instrument of Ireland? → "The harp"는 반복된 “Uilleann pipes”에 쉽게 영향 → EpU 높음 |
| 실험 구성 | - 모델: Gemini 1.0 Pro - 데이터셋: TriviaQA, AmbigQA (단일 정답), WordNet (다중 정답) - 비교법: Greedy logprob (T0), Semantic Entropy (S.E.), Self-verification (S.V.) |
| 주요 결과 | - 단일 정답 데이터셋: S.E. ≈ M.I. (모두 양호) - 혼합(단일+다중 정답): M.I. > S.E. (고 entropy 구간에서 recall ↑) - WordNet: M.I.와 S.E. 모두 우수하나, threshold tuning에서 M.I.가 더 안정적 |
| 장점 | ✅ Epistemic uncertainty만 추정 (aleatoric 제거) ✅ 추가 학습 필요 없음 (inference에서 prompt만 조작) ✅ black-box API 수준에서도 적용 가능 |
| 한계점 | ⚠ 반복 prompting 및 MI 추정의 계산 비용 큼 ⚠ semantic clustering 정확도, threshold 설정에 민감 ⚠ 정답이 여러 개인 쿼리에서 ground truth 정의의 모호성 존재 |
| 결론 및 기여 | - MI 기반 에피스테믹 불확실성 추정을 통해 LLM의 hallucination 여부를 정량화 가능 - 기존 first-order 방식의 한계를 극복 - 특히 다중 정답 환경에서 신뢰도 기반 abstention 정책 설계 가능 |
🔍 논문 핵심 요약표: To Believe or Not to Believe Your LLM
| 문제 정의 | 기존 불확실성 정량화(UQ) 방식은 에피스테믹과 알레아토릭 불확실성을 구분하지 못해, 여러 정답이 존재하는 경우(hallucination 포함) 대응이 어렵다. |
| 주요 목표 | 1. 에피스테믹 불확실성만 높은 경우를 감지 2. 이를 기반으로 LLM의 hallucination을 탐지 |
| 핵심 아이디어 | 동일한 질문에 대해 반복적으로 응답을 생성하고, 이전 응답들을 prompt에 추가하며 LLM의 응답 변화를 관찰함. → 응답들이 독립이면 알레아토릭, 종속이면 에피스테믹 불확실성으로 판단 |
| 방법론 요약 | 1. Iterative Prompting: - Q에 대해 Y₁, Y₂, ..., Yₙ을 순차적으로 생성하며 이전 응답을 다음 prompt에 포함 - 이로부터 LLM 기반 joint 분포 Q̃ 구성 2. 에피스테믹 불확실성 정량화: - Q̃와 실제 ground truth 분포 P̃ 간의 KL divergence를 정의 - 실제 P̃는 접근 불가하므로 mutual information |
| MI 추정 방법 | - 실제 joint 분포 관측이 어려우므로 샘플 기반 추정 - Stabilization (γ₁, γ₂) 사용 - 유사 응답을 semantic clustering하여 정규화 |
| 실험 설정 | - Gemini Pro 사용 - TriviaQA, AmbigQA (단일 정답 위주), WordNet (다중 정답) 데이터셋 활용 - 비교: Likelihood (T0), Semantic Entropy (S.E.), Self-verification (S.V.) |
| 결과 요약 | - 단일 정답 데이터셋에서는 S.E.와 거의 동등한 성능 - 혼합 데이터셋(단일 + 다중 정답)에서는 MI 기반 방식이 S.E.보다 월등함 - 특히 높은 entropy를 갖는 질의에서 recall이 뛰어남 |
| 추가 통찰 | - 반복 prompt에 의한 확률 증폭 설명 → LLM이 잘 아는 질문은 반복 정보에도 흔들리지 않음 → 잘 모르는 질문은 반복된 잘못된 응답에 영향을 받음 |
| 한계 및 향후 과제 | - MI 추정을 위한 반복 생성은 계산 비용이 높음 - multi-label ground truth의 정량적 정의가 더 필요 |
✨ 이해를 돕는 예시
Q: What is the national instrument of Ireland?
- 정답: “The harp” (0.936), 다른 응답: “Uilleann pipes” (0.063)
- “Uilleann pipes”를 반복해서 prompt에 넣으면 LLM이 “The harp”를 거의 출력하지 않게 됨
→ Epistemic Uncertainty가 크다 → Hallucination 가능성 높음
반면,
Q: What is the capital of the UK?
- 정답: “London” (≈1.0), 다른 응답: “Paris”
- “Paris”를 수십 번 반복해도 LLM은 “London”을 강하게 유지
→ Epistemic Uncertainty 낮음 → Hallucination 가능성 낮음
🔍 관련 연구 및 비교 요약
| 구분 | 방법론 요약 | 한계점 | 차이점 |
| 1. First-order methods | - 출력 분포의 log-prob, entropy 기반 - 하나의 응답 분포로부터 uncertainty 추정 |
- Aleatoric과 Epistemic 구분 불가 - 다중 정답 상황에서 hallucination 오탐지 |
- 본 논문은 multi-answer에서도 epistemic만 추정 가능 |
| 2. Self-verification (자기 검증) | - “이 응답이 맞는가?” 질문하여 log-prob("True") 사용 | - 모델 내부 신뢰 판단에 의존 (과잉 신뢰 가능) | - 본 논문은 모델 자체 출력을 이용, 더 이론적인 정당성 부여 |
| 3. Semantic Entropy | - 의미적으로 유사한 답변들을 클러스터링 후 entropy 계산 | - 여전히 1차 분포 기반 (first-order) - epistemic vs aleatoric 구분 어려움 |
- 본 논문은 joint distribution 기반 MI 추정으로 epistemic만 정량화 |
| 4. Conformal Prediction / Abstention | - 정답 포함 여부 기반의 abstention 설계 | - Strong assumption 요구 (exchangeability 등) | - 본 논문은 LLM 구조 활용해 반복 prompting으로 직접 불확실성 유도 |
| 5. Iterative Prompting 기반 | - 질문을 반복하거나 justification 유도 후 응답 신뢰성 향상 시도 | - 답변 품질 향상 목적, 불확실성 정량화는 아님 | - 본 논문은 반복 prompting을 불확실성 측정 수단으로 사용 |
| 6. Response Pair Training | - (query, answer₁, answer₂) tuple로 학습하여 epistemic 추정 | - 학습 변경 필요, 실시간 적용 어려움 | - 본 논문은 추가 학습 없이 inference 단계에서 MI로 평가 가능 |
| 7. Epistemic Neural Nets (EpiNets) | - 학습 시 다수의 모델 또는 randomness를 삽입하여 epistemic 추정 | - LLM에 적용 어려움, 파라미터 많음 | - 본 논문은 LLM을 블랙박스로 사용 가능함 |
| 8. Internal State 기반 분석 | - hidden state 분석을 통한 truth 여부 추정 | - 내부 접근 필요 (open weight 필요) | - 본 논문은 외부 출력만 이용한 접근, API 수준에서도 활용 가능 |
✨ 정리
- 기존 연구는 1차 분포(logprob, entropy 등) 또는 응답 자체를 판단하는 방식(self-verification)에 머물렀습니다.
- 본 논문은 LLM의 반복 출력 변화를 추적하여, 응답들 간의 종속성(MI)을 이용한 에피스테믹 불확실성 정량화를 시도합니다.
- 특히 multi-answer 환경에서 hallucination을 정확히 감지할 수 있는 희소한 접근으로, 이론적 타당성과 실용성을 모두 확보했습니다.
🔧 핵심 방법론 요약: Epistemic Uncertainty 추정 via Iterative Prompting + Mutual Information
🔍 1. 문제 설정 및 개념 정의
- Epistemic Uncertainty (EpU): 모델이 "잘 모르는 경우" (지식 부족, 학습 미흡 등)
- Aleatoric Uncertainty (AlU): 문제 자체에 정답이 여러 개 있는 불확실성
✅ 목표: 모델의 응답에서 epistemic uncertainty만 추정 → hallucination 탐지에 활용
🧠 2. 핵심 아이디어: 반복 프롬프트를 통한 불확실성 확대
🔁 Iterative Prompting:
- 기본 아이디어: 같은 질문을 여러 번 하되, 이전 응답들을 prompt에 포함시켜서 계속 묻는다
- LLM의 응답이 이전 응답에 따라 바뀐다면 → 그만큼 epistemic uncertainty가 높다
✅ 정식화:
- 질문 x에 대해 LLM이 응답 Y_1 생성
- 다음 prompt는:→ 이때 나온 응답을 Y_2
- Q: x One answer is: Y₁ Another answer is:
- 반복적으로 Y_1, Y_2, ... Y_n 생성
이 과정을 통해, LLM으로부터 pseudo joint distribution Q~(Y_1,...,Y_n∣x)을 구축
📊 3. 불확실성 정량화: Mutual Information (MI) 기반 측정
🎯 핵심 지표:
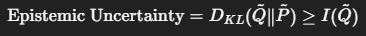
- Q~: 반복 prompting으로 얻은 모델의 joint 분포
- P~: ground truth 분포 (정답들이 독립이라고 가정)
- 실제로는 P~를 모르기 때문에, 하한선인 MI를 사용
💡 Mutual Information 의미:

📌 예시: “What is the capital of the UK?”
1. 질문:
Q: What is the capital of the UK?
2. 모델 응답:
| Prompt 버전 | 응답 | 비고 |
| 원 질문만 | "London" (0.999) | 정답 |
| + “Another answer is Paris” | 여전히 “London” 출력 (0.96 이상 유지) | EpU 낮음 |
| + “Paris” 여러 번 반복 | “Paris” 확률 증가하지만, “London” 유지 | 여전히 신뢰 가능 |
→ Epistemic Uncertainty 낮음
📌 예시 2: “What is the national instrument of Ireland?”
- 가능한 답: “The harp” (0.936), “Uilleann pipes” (0.063)
| 반복 프롬프트 | 출력 변화 |
| “Uilleann pipes” 반복 | “The harp” → 확률 급격히 낮아짐, 사라짐 |
→ Epistemic Uncertainty 높음 → hallucination 발생 가능성 큼
🔬 4. 실험적 구성 및 적용
- 사용 모델: Gemini 1.0 Pro (Google)
- 데이터셋:
- TriviaQA, AmbigQA: 단일 정답 위주
- WordNet 기반 쿼리: 다중 정답 → aleatoric uncertainty 존재
- 불확실성 측정 방식 비교:
- Greedy log-prob (T0)
- Semantic Entropy (S.E.)
- Mutual Information (M.I.) → 본 논문 제안
→ 다중 정답 문제에서 M.I. 방식이 유일하게 hallucination을 잘 탐지함
✅ 요약 정리
| 방법 | 반복 프롬프트를 통해 joint 분포 추정 후 Mutual Information 계산 |
| 핵심 지표 | |
| 목적 | Aleatoric uncertainty는 제거하고 Epistemic uncertainty만 추정 |
| 효과 | 모델의 hallucination 가능성 판단, abstention 정책 설계 가능 |
✅ 1. 실험 결과 요약 (Section 6)
| 모델 | Gemini 1.0 Pro |
| 데이터셋 | - TriviaQA (50K 샘플) - AmbigQA (12K) - WordNet 기반 다중 정답 데이터 (6K) |
| 비교 Baselines | ① Greedy logprob (T0) ② Semantic Entropy (S.E.) ③ Self-Verification (S.V.) |
| 제안 기법 | Mutual Information 기반 MI 추정 (M.I.) |
📊 주요 실험 결과
- 단일 정답 쿼리 (TriviaQA, AmbigQA):
- S.E.와 M.I.가 거의 동일 성능 (높은 정밀도, 높은 recall)
- T0와 S.V.는 열등함
- 다중 정답 쿼리 (WordNet):
- M.I.와 S.E. 모두 높은 성능 (정답은 항상 포함됨)
- 혼합 쿼리 (TriviaQA + WordNet, AmbigQA + WordNet):
- M.I.가 S.E. 대비 확연히 우수
- 특히 고 entropy 쿼리에서 recall이 월등함
- → 다중 정답 상황에서 S.E.는 threshold tuning이 어려움
- Calibrated Threshold 실험 (Figure 6):
- M.I. 방식은 entropy가 높은 쿼리에서도 낮은 에러율 유지
- S.E.는 높은 entropy 구간에서 거의 abstain (recall ↓)
🧾 2. 결론 (Section 7)
| 주장 | - LLM의 에피스테믹 불확실성을 Mutual Information으로 정량화 가능 - 이로써 hallucination 탐지가 정확히 가능해짐 |
| 혁신점 | - 기존 entropy/logprob 기반 first-order 방법의 한계를 극복 - Aleatoric 불확실성과 Epistemic 불확실성을 분리함 |
| 실용성 | - 추가 학습 없이, black-box API 수준에서 반복 prompting만으로 평가 가능 |
| 추가 통찰 | - 반복된 잘못된 응답을 넣으면 모델이 따라가려는 경향이 있음 → 모델이 해당 지식에 자신 없는 것의 증거 |
⚠️ 3. 한계점 및 향후 과제
| 💻 계산 비용 | - 반복 prompting 및 MI 추정은 시간·자원 비용 큼 (k개 샘플 필요) - inference 단계에서 여러 번 sampling 필요 |
| 🧠 MI 추정 정확도 | - MI는 ground-truth joint 분포 P~를 직접 알 수 없기 때문에 하한선만 사용 - Estimation bias 존재, 특히 낮은 sample 수에서는 안정성 문제 |
| 📐 Threshold 설정 | - Hallucination 탐지 정확도는 MI threshold λ 설정에 민감 → calibration 필요 |
| ✨ Semantic Clustering 의존성 | - 의미적 유사도 판단 (F1, cosine 등) 방식이 성능에 영향을 줌 - 긴 응답일수록 클러스터링 정확도 ↓ |
| 🧪 다중 정답 정의 | - 정답이 "여러 개"일 때의 ground truth 정의가 모호할 수 있음 - 특히 open-domain QA나 주관적 질문에서는 정답 불확실성 존재 |
🧠 핵심 요약
- 기여: LLM 응답의 종속성(MI)을 활용하여 epistemic uncertainty만 정량화한 새로운 접근
- 강점: 다중 정답 상황에서도 hallucination 감지 가능
- 한계: 계산 비용, threshold 튜닝, 의미적 클러스터 정의 필요
'인공지능 > 논문 리뷰 or 진행' 카테고리의 다른 글
| L2M - Least-to-Most Prompting Enables Complex Reasoning in Large Language Models (2) | 2025.05.13 |
|---|---|
| Decomposed Prompting: A Modular Approach for Solving Complex Tasks (0) | 2025.05.12 |
| Uncertainty 논문 모아 보기 NAACL 2025 - 4 (0) | 2025.05.07 |
| Planning 논문 모아 보기 NAACL 2025 - 3 (1) | 2025.05.03 |
| Agent, Hallucination 관련, Planning 논문 모아 보기 NAACL 2025 - 2 (5) | 2025.05.02 |
