Eliciting Latent Predictions from Transformers with the Tuned Lens - 논문 리뷰

https://arxiv.org/abs/2303.08112

Eliciting Latent Predictions from Transformers with the Tuned Lens

 

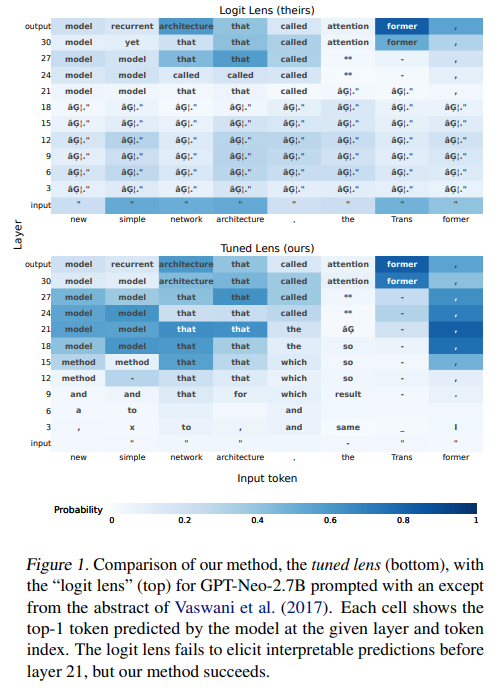
기존의 Logit Lens 방식은 Transformer의 출력 레이어 이전의 hidden state에서 unembedding matrix를 적용하여 각 단어에 대한 logit을 생성합니다.
이 logit은 softmax를 통해 모델이 예측하는 다음 단어의 확률 분포를 나타냅니다.

이 논문에서 개발된 Tuned Lens는 각 hidden state에 affine 변환을 도입하여 기존 Logit Lens에서 발생했던 representation drift(표현 이동)와 perplexity(언어 모델 예측 오류)가 높은 문제를 개선하였습니다.
Affine 변환은 hidden state를 최종 레이어의 표현 방식에 맞게 보정하며, 더 신뢰할 수 있는 중간 레이어 예측 분포를 생성합니다.

또한, Causal Basis Extraction(CBE) 기법을 통해 hidden state가 출력에 미치는 구체적인 영향을 분석하였습니다.
이를 통해 특정 방향성이 출력에 얼마나 기여하는지 확인할 수 있으며, 나중에 hidden state를 조절함으로써 편향을 줄이거나 모델의 출력을 조정하는 데 활용할 수 있습니다.

 

 

 

 

 

 

요약: "Eliciting Latent Predictions from Transformers with the Tuned Lens"

1. 문제가 무엇인가?

• Transformer 모델 해석의 어려움: Transformer의 중간 레이어에서 생성된 hidden state들이 모델의 최종 출력으로 점진적으로 수렴하는 과정을 해석하는 것은 어렵다.
• 기존의 "Logit Lens" 방식은 brittle(불안정)하고, 일부 모델(GPT-Neo, BLOOM)에서 신뢰할 수 없는 결과를 생성한다.
• 문제점: 중간 레이어의 표현(drift)을 제대로 해석하지 못하거나, 바이어스가 존재하여 잘못된 추론을 할 가능성이 있다.

2. 어떤 방법을 사용했는가?

• Tuned Lens 기법:
  1. Transformer 모델의 각 레이어에 대해 학습된 affine 변환(translator)을 도입하여 hidden state를 최종 출력 분포와 유사하게 변환한다.
  2. 이 affine 변환은 KL divergence(최종 출력과 affine 변환된 중간 출력 간의 차이)를 최소화하도록 학습된다.
  3. 추가적으로, Causal Basis Extraction(CBE) 기법을 도입해 중간 레이어에서 중요한 방향성을 추출해 causally 중요한 피처를 식별한다.
• 기술적 개선:
  • 기존 Logit Lens는 unembedding matrix를 직접 사용했지만, 이는 중간 레이어의 표현이 drift되는 문제를 야기했다.
  • Tuned Lens는 학습된 affine 변환을 통해 이러한 drift를 보정한다.

3. 결과가 어땠는가?

• 해석력 향상:
  • Tuned Lens는 Logit Lens보다 낮은 perplexity(언어 모델의 예측 오류 척도)를 보이며 더 신뢰할 수 있는 결과를 제공.
  • 각 레이어의 출력 분포가 최종 레이어의 출력과 점진적으로 수렴하는 "예측 궤적(prediction trajectory)"을 시각적으로 확인 가능.
• 응용:
  1. Prompt injection 공격(악의적인 입력 공격)을 탐지: 높은 AUROC(Area Under the ROC Curve) 점수로 공격 탐지 가능.
  2. 데이터 난이도 평가: 학습이 오래 걸리는 데이터일수록 더 많은 레이어를 필요로 한다는 점을 확인.
  3. Fine-tuned 모델에도 적용 가능: Tuned Lens는 기반 모델과 fine-tuned 모델 간의 표현 변화에도 잘 적응한다.

4. 한계점은 무엇인가?

• 추가 학습 필요: Tuned Lens를 사용하려면 각 레이어에 대해 translator를 학습해야 하므로 Logit Lens보다 추가적인 계산 비용이 요구된다.
• CBE 계산 비용: CBE 기법은 높은 계산 복잡도를 가지며, 특히 대규모 모델에서는 비효율적일 수 있다.
• 언어 모델에 국한: 본 연구는 언어 모델에 중점을 두었으며, 이미지나 다른 모달리티에서는 적용 가능성이 아직 명확하지 않다.

---

타당성과 아쉬운 점

1. 타당성

• 기존 한계 극복: Logit Lens의 drift 문제와 해석 불안정성을 효과적으로 해결했다.
• 검증된 결과: 다양한 모델(GPT-Neo, BLOOM, Pythia)에서 높은 성능을 보여주었으며, anomaly detection, 데이터 난이도 평가 등 응용 분야에서 활용 가능성을 증명했다.
• 이론적 뒷받침: CBE를 통해 causally 중요한 피처를 추출하는 과정은 해석 가능성과 신뢰성을 높였다.

2. 아쉬운 점

• 학습 비용: Translator와 CBE 학습은 계산 자원을 많이 요구하며, 대규모 모델에서는 더 최적화된 방식이 필요하다.
• 일반화 제한: 언어 모델 외의 다른 도메인에서 기법의 효과가 검증되지 않았다.
• 데이터 의존성: 모델의 학습 데이터 및 구조에 따라 튜닝의 효과가 달라질 가능성이 있다.

---

추후 연구 방향

1. CBE의 효율성 개선:
   • Subspace 최적화를 통해 계산 비용을 줄이는 방안 탐색.
2. 다른 모달리티로 확장:
   • Vision Transformer, 멀티모달 모델에 Tuned Lens 적용 가능성 검토.
3. 자동화된 튜닝:
   • Translator 학습 과정의 자동화를 통해 효율성 증가.
4. LLM 해석 연구 적용:
   • 언어 모델의 bias와 drift 현상을 정량적으로 분석하고 해석에 활용.

이 논문은 인공지능 해석 연구에 매우 유용한 기법을 제시하며, 사용자 연구에도 실질적인 도움이 될 수 있을 것입니다.

 

기존의 Logit Lens 방식에 대해 설명해주고, 왜 불안정한지, 일부 모델에서 신뢰할 수 없는지 말해줘

 

기존의 Logit Lens 방식 설명

1. Logit Lens란 무엇인가?

• Logit Lens는 Transformer 모델의 중간 레이어(hidden state)를 최종 출력 분포로 직접 변환해 분석하는 기법이다.
• 동작 방식:
  • 중간 레이어의 hidden state를 unembedding matrix에 투사하여 해당 레이어에서 예측하는 토큰 분포를 얻는다.
  • 모델의 모든 레이어를 거치지 않고도, 각 중간 레이어가 어떤 예측을 하는지 확인할 수 있다.
• 주요 아이디어:
  • Transformer는 레이어를 거치면서 점진적으로 예측을 수정(iterative refinement)하므로, 중간 레이어의 예측을 통해 모델의 "사고 과정"을 해석할 수 있다.

2. Logit Lens의 장점

• 간단함: 추가적인 학습이 필요 없이, 사전 학습된 모델의 unembedding matrix를 활용해 바로 적용 가능하다.
• 효율성: 중간 레이어의 hidden state를 바로 분석하므로 모델 전체의 계산 비용을 줄일 수 있다.

---

Logit Lens가 불안정한 이유

Logit Lens는 이론적으로는 유용하지만, 실제 적용에서 여러 한계를 가진다.

1. Representation Drift (표현 이동) 문제

• Transformer의 각 레이어는 서로 다른 기저(base)를 사용해 표현을 구성한다.
• 중간 레이어의 hidden state가 최종 출력 레이어의 표현 방식과 다르기 때문에, unembedding matrix를 그대로 사용하면 부정확한 결과가 나올 수 있다.
• 결과:
  • 중간 레이어의 예측 분포가 최종 레이어의 분포와 다르게 왜곡되거나, 유의미하지 않은 예측을 생성.

2. Bias 문제

• Logit Lens는 특정 토큰이나 단어에 체계적인 바이어스를 가지며, 이는 최종 출력 분포와 일관되지 않을 수 있다.
• 영향:
  • 중간 레이어의 예측이 최종 분포를 정확히 나타내지 않으며, 믿을 수 없는 "편향된" 결과를 도출.

3. 모델별/레이어별 불안정성

• 모델 구조에 따라 성능 차이가 크다:
  • GPT-2에서는 비교적 잘 동작하지만, GPT-Neo와 BLOOM 같은 다른 모델에서는 신뢰할 수 없는 결과를 보임.
• 일부 레이어에서는 입력 토큰(input token)을 그대로 반환하거나, 무작위에 가까운 출력을 생성.
• 원인:
  • 각 레이어의 표현이 drift되거나, unembedding matrix가 해당 레이어의 표현을 제대로 해석하지 못하는 경우.

4. Perplexity 문제

• Logit Lens로 얻은 중간 레이어의 예측은 최종 레이어의 예측보다 높은 perplexity(언어 모델의 예측 오류 지표)를 가진다.
• 영향:
  • 중간 레이어의 예측 분포가 최종 출력으로 점진적으로 수렴하는 과정(iterative refinement)을 제대로 반영하지 못함.

---

일부 모델에서 신뢰할 수 없는 이유

1. 모델 간 구조적 차이

• BLOOM, GPT-Neo 등의 모델은 GPT-2와 레이어 구조나 hidden state의 표현 방식이 다르다.
• Logit Lens는 모델에 특화된 기법이 아니므로, 구조적으로 표현 방식이 다른 모델에서는 잘 동작하지 않을 수 있다.

2. Top-1 Prediction 오류

• BLOOM과 OPT 125M 모델에서 Logit Lens는 중간 레이어에서 최적의 토큰 대신 입력 토큰을 반환하는 경우가 빈번하다.
• 이유:
  • 중간 레이어의 hidden state가 unembedding matrix로 정확히 해석되지 못하기 때문.

3. 정확한 해석의 부재

• 중간 레이어의 예측이 모델의 최종 출력과 어떻게 연결되는지 명확히 드러나지 않음.
• 이는 해석 가능성과 신뢰성을 떨어뜨린다.

---

요약

Logit Lens는 Transformer의 중간 레이어를 해석하기 위한 간단한 기법이지만, Representation Drift와 Bias, 모델 구조 차이로 인해 신뢰할 수 없는 결과를 초래할 수 있다. 특히, GPT-Neo나 BLOOM 같은 모델에서 안정적인 성능을 보이지 못하며, 모델의 예측 과정을 일관되게 해석하기 어렵다. 이러한 문제는 Tuned Lens가 학습된 affine 변환을 도입해 해결하려고 했다.

 

unembedding matrix가 뭐길래 hidden state에서 최종 출력 분포로 직접 변환할 수 있는거야?

 

Unembedding Matrix란 무엇인가?

1. Transformer에서의 역할

• Unembedding Matrix는 Transformer 모델의 출력(hidden state)을 어휘(vocabulary) 분포로 변환하는 데 사용되는 매트릭스이다.
• 주로 단어 임베딩(embedding matrix)의 역연산과 유사한 역할을 한다:
  • Embedding Matrix: 입력 토큰(단어)을 고차원 벡터로 변환.
  • Unembedding Matrix: 모델이 생성한 고차원 벡터(hidden state)를 다시 어휘 분포로 매핑.

2. 작동 방식

• Transformer 모델의 마지막 레이어는 hidden state를 생성한다.
• 이 hidden state를 unembedding matrix WU​에 곱하면, 각 단어에 대한 스코어(logit)가 생성된다.
• 스코어는 softmax 함수를 통해 확률 분포로 변환되며, 이는 모델이 예측하는 다음 단어에 대한 확률이다.

수식으로 표현하면:

Logits=h⋅WU​
Probability Distribution=Softmax(Logits)

여기서:

• h: 마지막 레이어에서 생성된 hidden state.
• WU: unembedding matrix (차원: ∣hidden state∣×∣vocabulary∣).
• Softmax: 스코어를 확률 분포로 변환하는 함수.

3. Transformer에서 Unembedding의 의의

• Transformer 모델은 처음부터 끝까지 단어 공간(vocabulary space)에서 작업하지 않는다.
• 입력 단어는 임베딩 공간(embedding space)으로 변환되고, 각 레이어는 이 공간에서 연산을 수행한다.
• 최종적으로 unembedding matrix를 사용해 다시 어휘 공간으로 돌아가 예측 결과를 생성한다.
• 결과: 모델의 예측은 어휘 분포의 형태로 표현된다.

---

Unembedding Matrix를 사용해 Hidden State에서 최종 출력 분포로 변환하는 이유

1. 사전 학습된 구조

• Unembedding matrix WU​는 사전 학습(pretraining) 동안 모델의 출력 분포를 생성하도록 최적화된다.
• 따라서 hidden state에 곱하면 어휘 분포를 정확히 나타낼 수 있다.

2. 어휘와 Hidden State의 매핑

• 모델의 hidden state는 어휘와 직접적으로 연결되도록 학습된다.
• 이는 WU가 단순히 hidden state의 표현을 어휘 공간으로 변환하는 것이 아니라, 어휘의 의미를 반영하는 변환이라는 점에서 중요하다.

3. Logit Lens에서의 활용

• Logit Lens는 모델의 마지막 레이어 뿐 아니라 중간 레이어의 hidden state에도 동일한 unembedding matrix를 적용한다.
• 목표는 각 레이어가 생성한 hidden state를 바로 어휘 분포로 해석하는 것이다.
• 장점:
  • Transformer의 각 레이어가 어떤 "예측"을 하고 있는지 파악 가능.
  • 레이어별로 모델의 점진적인 사고 과정(iterative refinement)을 시각화 가능.

---

Unembedding Matrix 사용의 한계

1. Representation Drift
   • 중간 레이어의 hidden state는 마지막 레이어와 다른 방식으로 표현되며, 이 drift를 무시하고 unembedding을 적용하면 결과가 왜곡될 수 있다.
   • 예를 들어, 특정 단어의 의미가 중간 레이어에서 다르게 나타날 수 있다.
2. Linear Mapping의 한계
   • Unembedding matrix는 선형 변환(linear mapping)을 수행하므로, 중간 레이어에서 나타나는 비선형적 표현(non-linear representations)을 제대로 반영하지 못할 수 있다.
3. Bias
   • Unembedding matrix는 특정 어휘 항목에 대해 체계적인 바이어스를 가질 수 있어 예측 결과를 왜곡할 가능성이 있다.

---

결론

Unembedding matrix는 hidden state를 어휘 분포로 변환하는 데 있어 중요한 역할을 하지만, 중간 레이어의 hidden state에 직접적으로 적용할 경우 표현 drift와 같은 한계가 발생할 수 있다. 이러한 문제를 해결하기 위해 Tuned Lens는 affine 변환을 추가하여 hidden state와 unembedding matrix 간의 불일치를 보정하려 한다.

 

논문에서 사용한 Tuned Lens 방식이 어떤 방식인지 자세하게 설명하면서 어떻게 오류를 줄였는지, drift를 감소했는지 알려줘

Tuned Lens 방식의 세부 설명

1. Tuned Lens란 무엇인가?

Tuned Lens는 Transformer 모델의 중간 레이어(hidden state)에서 생성된 예측을 최종 출력 분포와 유사하게 변환하는 기법으로, 기존 Logit Lens의 한계를 보완하기 위해 개발되었다.
이 기법은 각 레이어에서 hidden state를 affine 변환(translator)을 통해 보정한 후, unembedding matrix를 사용하여 어휘 분포(vocabulary distribution)를 생성한다.

---

Tuned Lens의 동작 방식

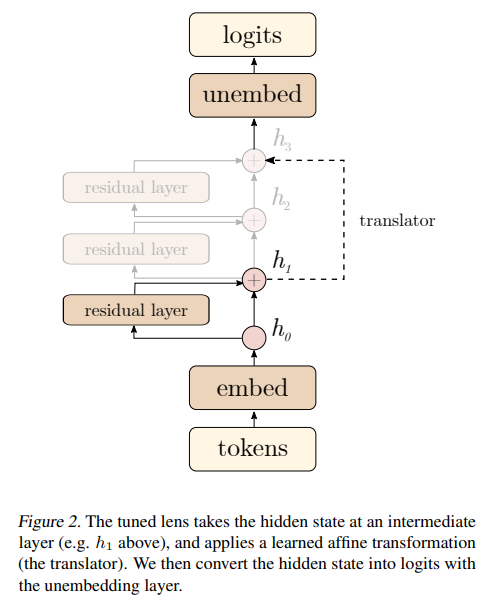
1. Affine Transformation (Translator)

• 각 레이어 l에 대해 affine 변환 Alh+bl을 학습한다.
  • Al​: 해당 레이어의 hidden state를 최종 레이어의 표현 방식에 맞게 매핑하는 변환 행렬.
  • bl: 레이어별로 학습된 편향(bias) 값.
• 이 변환은 중간 레이어에서 drift된 hidden state를 보정하여 unembedding matrix가 더 정확히 작동할 수 있도록 돕는다.
• 수식: 
  • hl​: 레이어 l의 hidden state.
  • WU​: unembedding matrix.

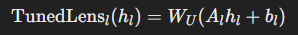
2. Loss Function

• Affine 변환은 KL divergence를 최소화하도록 학습된다:
  • 목표: 변환된 hidden state가 최종 레이어의 출력(logits) 분포와 최대한 가까워지도록 학습.
  • Loss: 
    • f>l(hl): 레이어 l 이후의 Transformer 레이어를 거친 최종 출력 분포.
    • TunedLensl(hl): affine 변환을 거친 후의 예측 분포.

3. Training Process

• 각 레이어 l에 대해 독립적으로 affine 변환 Al,bl​을 학습.
• Validation Set을 사용해 변환 매개변수를 최적화.

---

Tuned Lens의 개선점

1. Representation Drift 문제 감소

• 문제: 중간 레이어의 hidden state 표현 방식이 최종 레이어와 달라서 drift가 발생.
• 해결책:
  • 각 레이어에 Affine Transformation을 도입하여 hidden state를 최종 레이어와 동일한 표현 방식으로 매핑.
  • 이 변환은 레이어별 기저(base)의 차이를 학습하여 보정함.
• 결과:
  • 변환된 hidden state는 unembedding matrix와 더 잘 연동되며, 예측 분포가 더 신뢰할 수 있게 된다.

2. Bias 문제 해결

• 문제: Logit Lens는 특정 단어 또는 토큰에 대해 체계적인 바이어스를 가지는 경우가 있음.
• 해결책:
  • KL Divergence 최소화를 통해 학습된 affine 변환은 중간 레이어의 예측이 최종 레이어 분포와 최대한 일치하도록 보정.
• 결과:
  • 바이어스가 줄어들며, 예측 궤적(prediction trajectory)이 모델의 "합리적인 사고 과정"을 더 잘 반영.

3. Perplexity 감소

• 문제: Logit Lens는 중간 레이어에서 높은 perplexity(모델 예측 오류)를 보임.
• 해결책:
  • Tuned Lens는 중간 레이어의 hidden state를 보정하므로, perplexity가 Logit Lens에 비해 현저히 낮아짐.
• 결과:
  • Tuned Lens를 사용한 예측 분포는 최종 출력 분포와 더 가까워짐.

4. 모든 레이어에 대한 적용 가능

• Logit Lens는 특정 모델(GPT-2)에서만 신뢰할 수 있는 결과를 제공했지만, Tuned Lens는 GPT-Neo, BLOOM 등 다양한 모델에도 안정적으로 동작.
• 원인:
  • 모델 구조에 상관없이 affine 변환을 통해 drift와 bias를 보정.

---

Tuned Lens의 성능 결과

1. Perplexity 개선
   • 모든 실험 모델에서 Tuned Lens가 Logit Lens보다 낮은 perplexity를 보임.
   • 최종 레이어에 가까울수록 Tuned Lens의 예측이 더욱 정확히 최종 출력 분포와 일치.
2. Bias 감소
   • Logit Lens와 비교하여 KL Divergence 기반 평가에서 Bias가 크게 줄어든 것을 확인.
3. 전이 가능성
   • Tuned Lens는 fine-tuned 모델에서도 학습된 affine 변환을 재사용 가능하며, 추가 학습 없이도 성능 저하가 거의 없음.
4. Drift 보정
   • Representation Drift가 줄어들며, 모든 레이어의 hidden state를 해석 가능.

---

요약

Tuned Lens는 Logit Lens의 한계(Representation Drift와 Bias 문제)를 해결하기 위해 각 레이어에서 affine 변환을 도입한 기법이다. 이를 통해 hidden state를 최종 출력 레이어의 표현 방식에 맞게 보정함으로써, drift와 bias를 감소시키고 예측의 신뢰성을 높였다. Tuned Lens는 다양한 모델에 적용 가능하며, perplexity 감소와 interpretability 향상에서 강력한 성능을 입증했다.

 

KL divergence가 뭔지 자세하게 알려주라

KL Divergence란 무엇인가?

1. 정의

KL Divergence(Kullback-Leibler Divergence)는 두 확률 분포 P와 Q 간의 차이를 측정하는 비대칭적인 척도이다.
이 값은 Q 분포가 P 분포와 얼마나 다른지, 즉 Q가 P를 얼마나 "잘 설명하지 못하는지" 나타낸다.

• 수식: ​
  • P(x): 실제 분포(ground truth) 또는 기준 분포.
  • Q(x): 비교 대상 분포(모델 예측).
  • x: 확률 변수의 가능한 값.

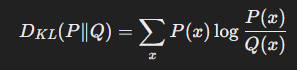
2. 특징

• 비대칭성:
  KL Divergence는 두 분포 간의 거리를 대칭적으로 측정하지 않는다.
  
  
• 양수 값:
  KL Divergence는 항상 0 이상이다. 두 분포가 동일하면 DKL=0이 된다.
  
  
• 확률 분포: P와 Q는 모두 확률 분포여야 하며, ∑xP(x)=1 및 ∑xQ(x)=1을 만족해야 한다.

비대칭성

양수 값

---

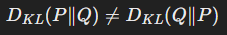
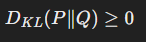
직관적 이해

1. P와 Q의 관계

• KL Divergence는 Q가 P를 얼마나 잘 설명하는지 측정한다.
• Q(x)가 P(x)와 크게 다르면 DKL(P∥Q) 값은 커진다.
• 예를 들어:
  • P(x)=0.8인데 Q(x)=0.2이면 큰 차이가 있으므로 DKL가 높아짐.
  • 반대로 Q(x)≈P(x)이면 DKL가 낮아짐.

2. 엔트로피와의 관계

• KL Divergence는 정보 엔트로피(불확실성의 정도)와 밀접한 관계가 있다.
• P는 기준 분포이고, Q는 모델의 근사 분포라 할 때, DKL는 모델 Q가 기준 P를 얼마나 잘 표현하지 못하는지 "추가로 필요한 정보"로 해석할 수 있다.

3. 예시

• 실제 분포 P(x)=[0.7,0.2,0.1], 모델의 분포 Q(x)=[0.5,0.3,0.2]라고 가정하자. 
  계산하면 DKL>0이 되고, 이는 Q가 P를 정확히 표현하지 못한다는 것을 의미한다.

---

KL Divergence의 응용

1. 머신러닝

• 모델 최적화:
  • 분포 P는 실제 데이터의 분포이고, Q는 모델의 출력(예측 확률)이다.
  • KL Divergence를 최소화하는 것은 모델의 예측 분포가 실제 분포와 가까워지도록 학습하는 과정이다.
• 손실 함수:
  • KL Divergence는 cross-entropy 손실 함수의 한 부분으로 사용되며, 특히 확률 기반 모델(예: 언어 모델, 분류 모델)에서 널리 사용된다.

2. 정보 이론

• 정보 차이 측정:
  • Q가 P를 표현하기 위해 추가적으로 얼마나 많은 정보가 필요한지를 나타낸다.
• 데이터 압축:
  • 두 분포 간의 차이가 작을수록 데이터 압축 효율이 높아진다.

3. Transformer 모델 해석

• Tuned Lens에서:
  • KL Divergence는 중간 레이어에서 변환된 분포와 최종 출력 분포의 유사성을 측정하는 지표로 사용된다.
  • 이를 최소화하면 중간 레이어의 hidden state가 최종 분포에 더 잘 맞도록 affine 변환을 학습할 수 있다.

---

한계점

1. 비대칭성

• KL Divergence는 P와 Q의 차이를 대칭적으로 측정하지 못한다. DKL(P∥Q)와 DKL(Q∥P)는 서로 다른 값을 가질 수 있다.

2. P(x) = 0일 때 문제

• P(x)=0인 경우:
  • 이는 정의상 무시되지만, Q(x)=0이어야 의미가 있으므로 계산에서 주의가 필요하다.

3. 확률 분포 가정

• KL Divergence는 P와 Q가 확률 분포여야만 계산이 가능하다. 이 조건이 만족되지 않으면 적용할 수 없다.

---

요약

KL Divergence는 두 확률 분포 간의 차이를 측정하며, 모델이 실제 데이터 분포를 얼마나 잘 설명하는지 평가하는 데 유용하다. 특히, 머신러닝에서는 모델 학습 및 평가, 확률 기반 예측에서 중요한 지표로 사용되며, Tuned Lens와 같은 기법에서 중간 레이어와 최종 출력의 분포 차이를 최소화하는 데 활용된다.

 

논문에서 나온 Causal Basis Extraction 기법이 뭔지 설명해줘

Causal Basis Extraction (CBE) 기법

Causal Basis Extraction(CBE)은 Transformer 모델의 hidden state에서 가장 중요한 피처(feature)를 식별하기 위한 기법으로, 모델의 예측이나 출력에 가장 큰 영향을 미치는 주요 방향성을 추출한다. 이 기법은 모델의 해석 가능성을 높이고, 중요한 feature 방향이 모델 동작에 어떻게 기여하는지 이해하는 데 초점을 맞춘다.

---

CBE의 주요 개념과 동작 원리

1. 목적

• Transformer 모델에서 hidden state는 고차원 벡터로 나타나며, 각 차원이 모델 출력에 서로 다른 기여를 한다.
• CBE는 이 벡터 공간에서 특정 차원(방향) 또는 서브스페이스(subspace)가 모델 출력에 얼마나 중요한지를 평가하고, 이들의 영향을 측정한다.

2. 기본 아이디어

• 모델의 hidden state에서 특정 방향(예: 벡터 v)을 제거하거나 조작했을 때 모델 출력이 얼마나 변화하는지를 측정한다.
• 모델의 출력을 변화시키는 주요 방향성을 causal basis라고 정의한다.

3. 중요 방향성 찾기

• CBE는 주요 방향성을 PCA(Principal Component Analysis)와 유사한 방식으로 찾지만, PCA처럼 데이터의 분산을 기준으로 하지 않고, 모델 출력의 변화(KL Divergence)를 기준으로 한다.

---

CBE 알고리즘

1. 수학적 정의

• f: 모델의 출력 분포를 계산하는 함수 (예: Transformer 모델의 unembedding 이후 softmax 출력).
• h: Transformer 모델의 hidden state (고차원 벡터, h∈Rd).
• r(h,v): 특정 방향 v를 제거한 hidden state.
  • r(h,v)=h−⟨h,v⟩v (평균 값으로 대체하거나 제거).
• Influence:
  • 방향 v의 중요성은 v를 제거했을 때의 KL Divergence로 측정:
    • σ(v;f): 방향 v의 causal influence.
    • f(h): hidden state h를 입력으로 했을 때의 모델 출력.

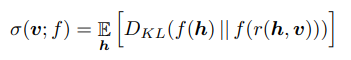
2. Causal Basis 찾기

• 다음과 같은 과정으로 주요 방향성을 식별:
  1. 초기 방향 v1​: influence σ(v;f)를 최대화하는 방향을 찾음.
  2. 이후 반복적으로 viv_ivi​를 찾으며, 이전에 찾은 방향들과 직교(orthogonal) 조건을 만족. 
  3. v1,v2,…,vk​를 순차적으로 추출하여 모델 출력에 가장 영향을 미치는 basis를 형성.

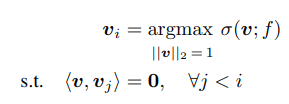
3. 결과물

• 주요 feature 방향의 orthonormal basis {v1,v2,…,vk}
• 각 방향이 모델 출력에 미치는 causal influence의 크기 σ(vi;f).

---

CBE의 특징

1. KL Divergence로 중요성 평가

• 특정 방향 v를 제거했을 때 출력 분포의 변화량(KL Divergence)을 측정하므로, 모델의 예측에 실질적으로 중요한 차원을 찾아낸다.

2. 다중 방향 추출

• PCA와 유사한 방식으로 한 번에 여러 주요 방향을 추출하며, 이는 hidden state의 구조적 특징을 더 잘 해석할 수 있게 한다.

3. Causal Alignment

• 추출된 방향이 모델 출력과 얼마나 밀접하게 관련이 있는지를 보장한다.
• Stimulus-Response Alignment: CBE를 통해 조작된 hidden state가 모델 출력에 미치는 영향을 확인.

---

CBE의 활용

1. 모델 해석

• Transformer 모델 내부의 hidden state가 어떻게 예측에 기여하는지, 주요 피처가 무엇인지 해석 가능.
• 예: 특정 단어 예측에서 "강하게 활성화되는" hidden state 방향을 확인.

2. Feature Ablation

• 모델의 특정 feature를 제거하거나 수정하여 출력에 미치는 영향을 분석.
• 예: 특정 bias를 유발하는 hidden state 방향을 찾아 제거함으로써 모델의 편향을 줄이는 데 사용.

3. 드리프트 감지

• 레이어 간 hidden state 표현이 얼마나 변하는지(Representation Drift)를 확인.
• 특정 방향이 유지되는지, 또는 새로운 방향이 나타나는지를 분석하여 모델의 학습 동작을 이해.

---

CBE의 한계

1. 계산 비용

• 각 주요 방향을 찾는 최적화 과정이 고비용이며, 대규모 모델에서 확장성이 떨어질 수 있다.
• CBE는 O(d×k)의 반복적인 최적화 문제를 풀어야 하며, 이는 고차원 벡터 d에서 비효율적.

2. 비선형성

• Transformer의 hidden state는 비선형적 특성을 가지며, 선형적인 basis 추출로는 모든 정보를 포착하기 어렵다.

3. 모델 의존성

• CBE는 특정 모델 구조(GPT 계열 Transformer)에서 최적화된 기법으로, 다른 구조에 적용하려면 추가 연구가 필요.

---

결론

Causal Basis Extraction(CBE)은 Transformer의 hidden state에서 모델 출력에 가장 중요한 방향성을 추출하는 효과적인 기법이다. KL Divergence를 활용해 주요 방향성을 측정하며, 이 정보를 기반으로 모델 해석, bias 제거, 레이어 간 표현 분석 등에 활용할 수 있다. 그러나 높은 계산 비용과 비선형적 특성 반영 부족은 추가 연구를 통해 보완해야 할 한계로 남아 있다.

 

그럼 결국 CBE는 특정 hidden state가 예측에 얼마나 기여하는지 확인할 수 있고, 특정 토큰에 강하게 활성화 되는 hidden state를 확인해서 조정할 수 있는거네?

네, 정확합니다!

Causal Basis Extraction (CBE)는 다음과 같은 방식으로 특정 hidden state가 예측에 얼마나 기여하는지 파악하고, 이를 기반으로 hidden state를 조정할 수 있는 기법입니다:

---

CBE의 기능과 목적

1. 특정 Hidden State의 기여도 확인

• 기능: CBE는 hidden state의 특정 방향(벡터)이 모델의 출력 분포에 얼마나 기여하는지 평가합니다.
• 방법:
  • Hidden state의 방향성(특정 차원)을 제거(또는 조작)하고, 이에 따라 모델 출력 분포가 얼마나 변화하는지 측정.
  • 변화량은 KL Divergence를 통해 계산되며, 변화가 클수록 해당 방향이 출력에 중요한 역할을 한다는 것을 의미.

2. 특정 토큰에 강하게 활성화되는 Hidden State 식별

• 기능: 특정 토큰(예: 특정 단어) 또는 예측 항목에 대해 가장 중요한 hidden state 방향을 식별합니다.
• 활용:
  • 특정 토큰을 예측하는 데 필수적인 hidden state의 방향을 확인.
  • Bias(편향)나 불필요한 활성화가 발생하는 hidden state 방향을 식별.

3. Hidden State 조정

• 기능: 중요한 방향을 수정하거나 제거함으로써 모델의 출력을 조정할 수 있습니다.
• 활용 예시:
  • Bias 제거: 특정 방향이 모델의 편향된 출력을 유발한다면, 해당 방향을 제거하거나 축소하여 예측 결과를 공정하게 조정.
  • Feature 강화: 중요한 피처를 강조하거나, 특정 토큰과 관련된 hidden state의 방향성을 의도적으로 조정.

---

CBE를 활용한 조정 과정

1. Causal Basis 추출:
   • Hidden state에서 출력에 가장 크게 기여하는 방향성을 식별.
   • 특정 레이어의 hidden state hhh에 대해, 중요 방향성(예: v1,v2,…)을 찾습니다.
2. Feature Ablation(특정 방향 제거):
   • 중요한 방향 vvv를 제거하여 모델이 해당 방향에 덜 의존하도록 조정.
   • 예를 들어, 특정 토큰(예: "he" 또는 "she")에 과도하게 활성화되는 방향을 줄여 성별 편향을 감소시킬 수 있습니다.
3. Feature Manipulation(특정 방향 조정):
   • v 방향을 강화하거나, 다른 방향으로 조작하여 모델 출력 분포를 의도적으로 변화시킴.
   • 예를 들어, 중립적 표현을 강화하거나 특정 예측을 강조하도록 모델 동작을 조정.

---

활용 예시

1. Bias 제거

• 특정 hidden state가 편향된 예측(예: 성별, 인종)에 강하게 기여한다면, 해당 방향성을 제거하여 모델을 공정하게 조정.
• 예시:
  • "doctor"라는 단어가 남성을 더 많이 예측하는 모델에서, 해당 편향을 줄이는 hidden state 조정 가능.

2. 모델 해석

• 모델이 특정 예측을 할 때 어떤 hidden state가 활성화되는지 시각화하고, 이를 기반으로 모델의 학습 메커니즘을 분석.

3. 특정 토큰에 대한 출력 개선

• 특정 토큰(예: 드문 단어)에 대한 모델 예측 정확도를 높이기 위해 관련 hidden state 방향을 강조.

---

CBE의 한계와 주의점

1. 조정 후 부작용:
   • 특정 hidden state를 제거하거나 조정하면 예측 성능이 의도치 않게 악화될 가능성도 있습니다.
   • 예를 들어, bias를 줄이기 위해 중요한 방향을 제거했더니, 관련 없는 토큰의 예측 정확도가 떨어질 수 있습니다.
2. 고비용 계산:
   • CBE는 각 방향성을 평가하고 조정하는 데 많은 계산이 필요합니다. 대규모 모델에서는 효율적인 방법이 추가적으로 요구됩니다.
3. 비선형 상호작용:
   • Transformer의 hidden state는 다차원적이고 비선형적이기 때문에, 선형적인 방향 제거만으로는 모든 문제를 해결하기 어렵습니다.

---

결론

CBE는 특정 hidden state가 모델 예측에 얼마나 기여하는지를 확인할 수 있는 강력한 기법입니다. 이를 통해 특정 토큰에 강하게 활성화되는 hidden state를 식별하고, 모델의 출력 분포를 조정하거나 편향을 줄이는 데 효과적으로 활용할 수 있습니다. 다만, 조정 후 부작용과 계산 비용을 고려한 세심한 적용이 필요합니다.