인공지능 backpropagation, optimization- 개념

backpropagation

backpropagation은 대부분의 인공지능의 파라미터 업데이트 방식이다.

경사하강법

우린 경사하강법을 통해 loss를 최소화 시키는 방향으로 학습한다.

activation function이 없는 FCN에서의 gradient decent 계산

기본적인 gradient 계산 방법이다. 

activation finction이 있는 NN에서의 backpropagation 방법이다.

이제 activation funcion(sigmoid, ReLU)와 여러 layer가 있는 NN에선 위와 같은 방식으로 backpropagation이 진행된다.

위 식을 하나 하나 풀어서 본다면 아래와 같은 식이 나온다.

여기선 activation이 identity이기 때문에 미분하면 1이 나왔다.

sigmoid가 추가되었다.

여기선 첫번째 레이어의 파라미터를 구할 수 있게 된다.

위 식들을 다 곱하면 이런 결과가 나온다.

출력층이 2개면 loss함수도 바뀌기 때문에 잘 판단해야 한다.

중간고사에 나왔었떤 문제

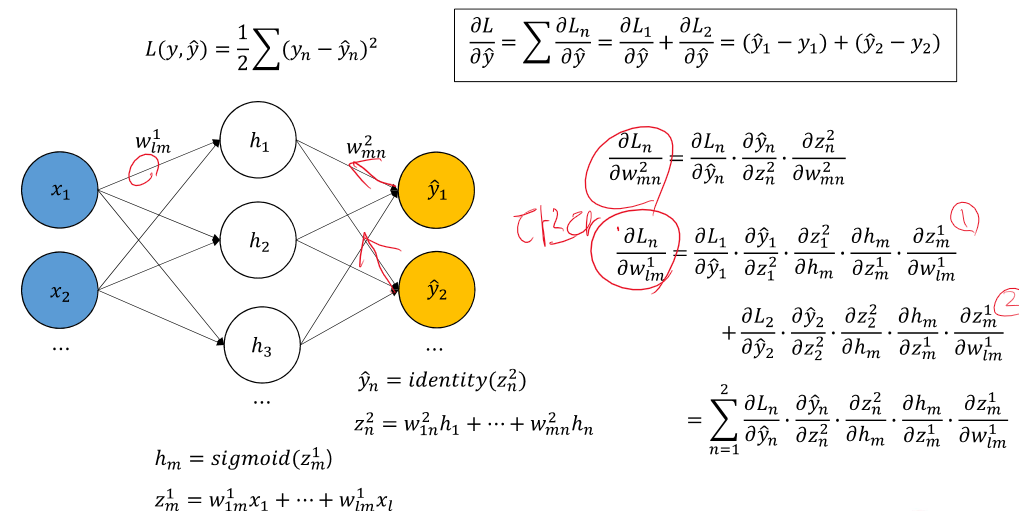
그럼 저렇게 구한 미분값을 통해 학습률을 곱해서 원래의 파라미터에 빼게 된다.

이제 이러한 backpropagation에 여러 요소들을 추가하여 만든 optimization을 보겠따.

728x90

optimization

학습 데이터를 나눔에 따라 바뀌는 것들.

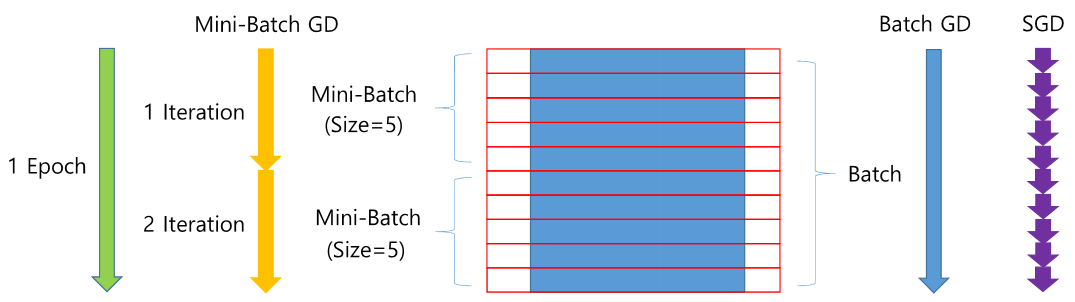
Batch GD는 파라미터를 업데이트하는데 모든 학습데이터를 다 넣은 다음에 한다.

SGD는 각각의 데이터마다 학습 파라미터를 업데이트하기 때문에 빠르지만 이상치의 영향이 크다.

miniBatch GD는 위의 두가지의 장점들을 각각 가지고 온 것이다.

Epoch는 이 학습의 총 반복 횟수이고, Iteration은 Epoch * Batch 개수 이다.

learning rate가 너무 클 경우 발생하는 오버슈팅

learning rate가 너무 크면 발산하기 때문에 점차 감소하여 수렴하게 하는 것이 중요하다.

global minimun point를 막는 saddle point

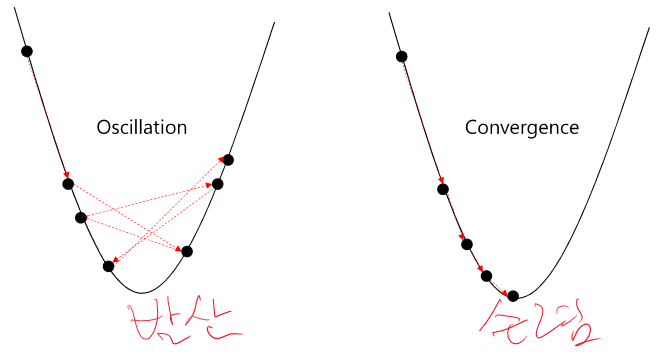
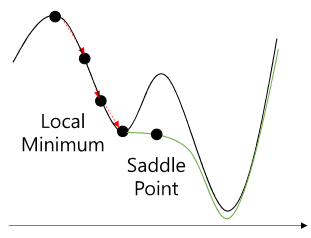
경사하강법을 통해 감소해가다가 전체에서 loss가 제일 작은 점이 아니라 saddle point에 의해 Local의 Minimum으로 빠질 수도 있다. 이것을 고치기 위해 많은 optimization이 나왔따.

SGD Momentum - Batch size가 1이 아니어도 된다. 이름만 SGD이다.

이 optimizer는 느린 학습, local minimum에 빠지는 것, 진동을 해결했다. Momentum은 속도의 역사(과거의 gradient를 기록하여 현재에 반)에 의해 계산된다.

Momentum 계산 과정

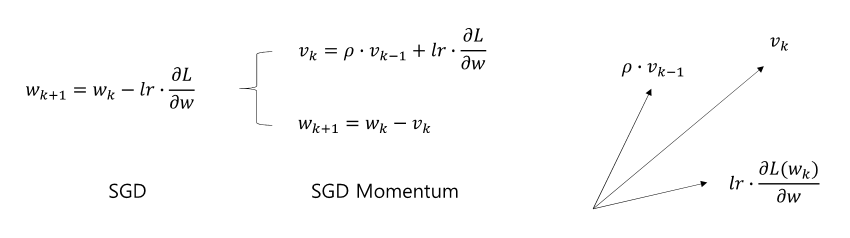
식 자체는 어려워 보이지만 roh(momentum) = 0.9 나 0.999이고, v0 = 0이다. 그러니까 쉽게 말하면 지금 로스와 이전의 로스의 누적값들을 더해서 그것을 파라미터에 빼는 형식이다. 

over shooting

이전의 누적값이 너무 커지면 (이전의 영향값이 너무 커지면) 오히려 global minimun을 벗어나는 일이 생길 수 있다.

Nesterov Momentum

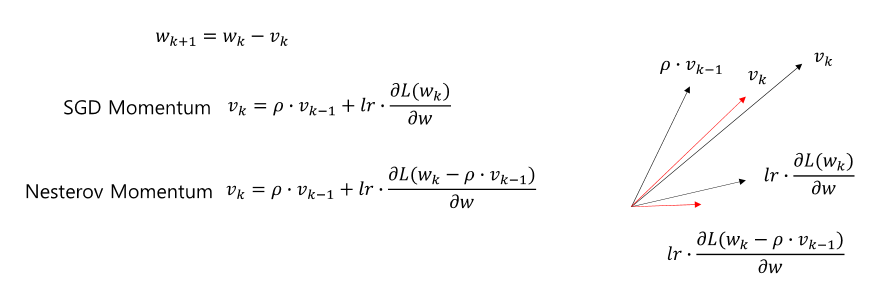
이 것을 해결하기 위해 나온 것이 Nesterov Momentum이다. 이 optimizer는 미리보기 기울기를 사용한다. 미리보기 기울기를 사용하여 overshooting을 평가하고 보다 정확하게 최적점에 도달하게 돕는다.

AdaGrad ( Adaptive gradient) - learning rate를 상황에 맞게 가지자

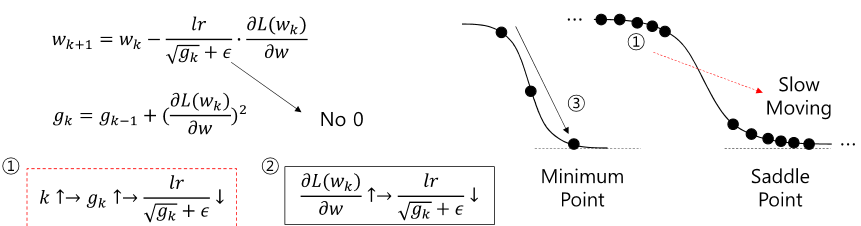
이 것은 상황에 맞게 learning rate를 바꿔서 초반엔 크게, 후반에는 작게 만들어 준다.
1. 이미 많이 움직였다면 조금만 움직인다. 반대 케이스라면 크게 움직인다.
2. gradient가 크다면 조금 움직인다. 반대 케이스라면 크게 움직인다.
3. 초반에 기울기가 크다면 학습이 빨리 끝난다. but 시간이 지남에 따라 학습률이 너무 감소하여 global minimun을 못 찾을 수 있다.

gk는 여태까지 기울기의 누적이고, e는 0이 되지 않기 위한 작은 값이다. 그래서 k(횟수)가 증가할수록 gk(누적값)이 증가하여 learning rate가 감소하되고, 기울기가 크다면 gk가 빨리 누적되어 learning rate가 감소하게 된다.

Root Mean Square Propagation

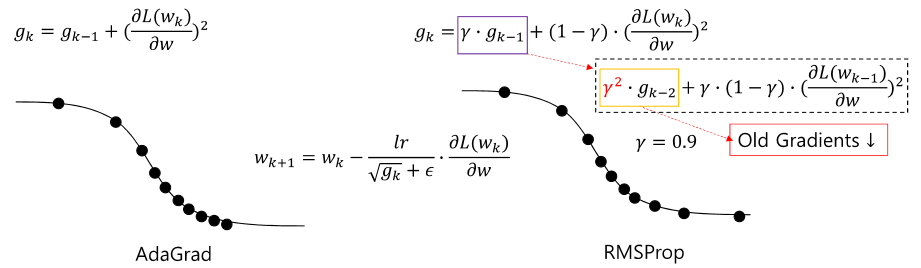
RMSPro은 AdaGrad의 공격적인 learning rate 감소를 막기 위해 나왔다. gk의 빠른 성장을 막기 위해 weighting factor(γ)을 사용하여 learning rate의 급격한 감소를 막고, 장기적으로 안정적인 학습을 도와준다.

weighting factor의 효과

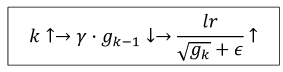
이것은 AdaGrad보다 최신의 gradient를 좀 더 중요시한다고 볼 수 있다.

이 RMSProp의 장점과 SGD Momentum의 장점을 합친 ADAM이 나오게 된다.

Adam

Adam은 SGD Momentum의 velocity와 RMSProp의 learning rate(gk)를 기본으로 parameter를 업데이트 한다.
β 1 =0.9, β2 =0.999, v0 =g0 =0으로 초기 값을 설정해준다.

좀 더 편하게 봐보쟈

위 식을 이렇게 보면 좀더 직관적으로 볼 수 있다. gk와 vk를 사용하여 이전의 이점을 모두 살렸지만 단점은 커버하여 각 매개변수에 대해 맞춤형 학습률을 적용하여 더 빠르고 안정적으로 global minimun에 도달할 수 있게 도와준다.