갑자기 코테를 보게 된.... 준비를 해봅시다...
백준 2579 계단문제



문제 처음 읽고 이게 무슨 문젠가 했네요....
검색해보니 계단을 시작부터 생각하지 말고 끝에서부터 생가하기!
내가 n 칸 일때 나는 n-1칸에 왔거나, n-2칸에서 왔습니다. 그러나 3칸 연속 오를 수 없다는 조건 때문에 n-1에서 온 경우 n-3에서 왔습니다. 그렇게 쭉쭉 풀어갑니다.
그래서 계단 저장할 배열 하나, 점수 저장할 배열 하나 만들어서 하나 하나 저장해가면 됩니다.
백준 1463 1로 만들기


결국 그리디 문제 아닌가요?
숫자가 주어지면 -1 or -2 or 그대로 가지고 가서 3으로 나누기!
아닌가?
11일 때
11 -> 10 -> 5 -> 4 -> 2 -> 1
11 -> 10 -> 9 -> 3 -> 1
8일때
8-> 4 -> 2 -> 1
8-> 7 -> 6 -> 3 ->2
아니네요
결국 1에서부터 천천히 숫자를 올리면서 진행하면 되는 코드였네요...
백준 9461 파도반 수

입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
예제 입력 1 복사
2
6
12
예제 출력 1 복사
3
16삼각형 변 구하는 거네요
오 규칙이 n을 구하는거면 n-2, n-3 번째 더하면 되네요?
맞았습니다.
백준 9184 신나는 함수 실행
문제
재귀 호출만 생각하면 신이 난다! 아닌가요?
다음과 같은 재귀함수 w(a, b, c)가 있다.
if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) returns:
1
if a > 20 or b > 20 or c > 20, then w(a, b, c) returns:
w(20, 20, 20)
if a < b and b < c, then w(a, b, c) returns:
w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c)
otherwise it returns:
w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1)
위의 함수를 구현하는 것은 매우 쉽다. 하지만, 그대로 구현하면 값을 구하는데 매우 오랜 시간이 걸린다. (예를 들면, a=15, b=15, c=15)
a, b, c가 주어졌을 때, w(a, b, c)를 출력하는 프로그램을 작성하시오.
입력
입력은 세 정수 a, b, c로 이루어져 있으며, 한 줄에 하나씩 주어진다. 입력의 마지막은 -1 -1 -1로 나타내며, 세 정수가 모두 -1인 경우는 입력의 마지막을 제외하면 없다.
출력
입력으로 주어진 각각의 a, b, c에 대해서, w(a, b, c)를 출력한다.
제한
- -50 ≤ a, b, c ≤ 50
예제 입력 1 복사
1 1 1
2 2 2
10 4 6
50 50 50
-1 7 18
-1 -1 -1
예제 출력 1 복사
w(1, 1, 1) = 2
w(2, 2, 2) = 4
w(10, 4, 6) = 523
w(50, 50, 50) = 1048576
w(-1, 7, 18) = 1이게 그냥 구현문제가 아니라 DP라구요...?
냅다 구현하면 시간 초과가 뜨네요
숫자마다 다 저장해놓고 일정 숫자가 나오면 그냥 바로 넘어가는 형식으로 해야 겠네요 ㅎㅎ,...
이 방식이 '메모이제이션'이라네요
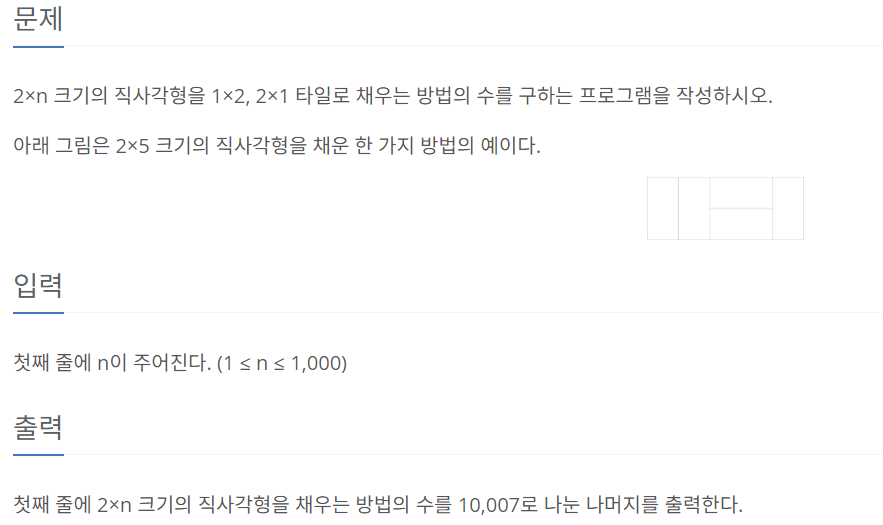
백준 11726 2*n타일링
예제 입력 1 복사
2
예제 출력 1 복사
2
예제 입력 2 복사
9
예제 출력 2 복사
55음 일단 홀수면 무조건 1개의 벽돌은 고정되어 있으니 홀수라면 전 숫자에 *2가 되겠네요
아니네요ㅜ
n[2] = 2, n[3] = 3, n[4] = n[2]*n[2]+1, n[5]= n[3]*n[2]
n[i] = n[i-1] + n[i-2]라는데 ...?
오.. 오지네요
i일 경우
[i-1] | , [i-2] = 이렇게 두 가지 경우 밖에 없네요 크게크게 보면 보였을 텐데 너무 숫자만 봤나 봅니다...
백준 11727 2*n 타일링 2

예제 입력 1 복사
2
예제 출력 1 복사
3
예제 입력 2 복사
8
예제 출력 2 복사
171
예제 입력 3 복사
12
예제 출력 3 복사
2731
그럼 이전 경험에 따르면 n[i] = n[i-1] + n[-2]*2 되겠네요
맞았습니당
백준 1932 정수 삼각형
문제
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5위 그림은 크기가 5인 정수 삼각형의 한 모습이다.
맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.
삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.
입력
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
출력
첫째 줄에 합이 최대가 되는 경로에 있는 수의 합을 출력한다.
예제 입력 1 복사
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
예제 출력 1 복사
30제가 제일 어려워하는 분야중 하나인데....
설마 이것도 제일 밑에서 하나씩 합쳐가면서 구현하나...?
밑에가 n개니까 n-1번씩 반복해서 n-1번 하기 오 좋다.
n = int(input())
dp = [[0 for _ in range(n + 1)] for _ in range(n + 1)]
for i in range(1, n + 1):
numbers = list(map(int, input().split())) # 한 줄의 숫자들을 입력받음
for j in range(1, i + 1):
dp[i][j] = numbers[j - 1] # 입력받은 숫자를 dp 배열에 저장
for i in range(n - 1, 0, -1): # 삼각형의 바닥부터 위로 올라가며 최대 합 계산
for j in range(1, i + 1):
dp[i][j] += max(dp[i + 1][j], dp[i + 1][j + 1])
print(dp[1][1])맞았는데 구현을 제대로 못했었네요 ㅎㅎ...ㅠ
노트북 베터리가 이제 거의 없어서 집가서 하겠습니다.
'알고리즘 > 코테 준비' 카테고리의 다른 글
| 코테준비 - 우선순위 큐 (1) | 2024.03.22 |
|---|---|
| 코테 준비 - 그래프 1 (1) | 2024.03.22 |
| 코테준비 - 분할정복 (1) | 2024.03.22 |
| 코테 준비 - 구현 1 (0) | 2024.03.22 |
| 코테 준비 - DP 2 실버 1 까지 (0) | 2024.03.21 |